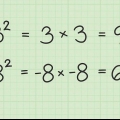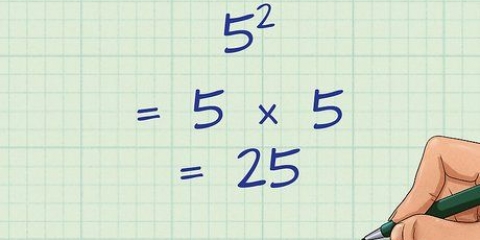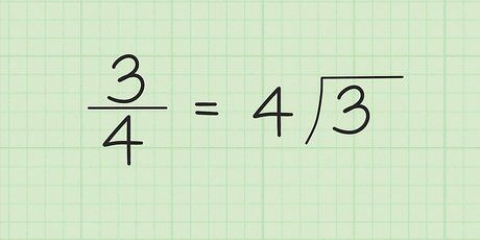Opdeling af kvadratrødder

Indhold

Trin
Tips
Advarsler

At dividere med kvadratrødder er i det væsentlige en forenkling af en brøk. Selvfølgelig gør tilstedeværelsen af kvadratrødder processen en smule mere kompliceret, men der er regler, der tillader os at arbejde med brøker på en forholdsvis nem måde. Det vigtigste at huske er, at du skal dividere koefficienter med koefficienter og rødder med rødder. Du bør heller aldrig efterlade en kvadratrod i en nævner.

Trin

Metode 1 af 4: Deling af gulerødder

1. Sæt brøken op. Hvis udtrykket ikke allerede er i form af en brøk, så omskriv det sådan her. Dette gør det lettere at følge alle de nødvendige trin for at dividere med en kvadratrod. Husk, at et divisionstegn er det samme som en brøklinje.

Hvis du f.eks $\sqrt{144} \div \sqrt{36}$ ${sqrt{144}}div {sqrt{36}}$ beregner, og omskriv derefter problemet som: $\frac{\sqrt{144}}{\sqrt{36}}$ ${frac{{sqrt{144}}}{{sqrt{36}}}}$ .

Billede med titlen Divide Square Roots Trin 2

2. Brug et radikalt tegn. Hvis dit problem har en kvadratrod i tælleren og nævneren, kan du placere begge rødder under en radikal. (En rod er tallet under radikalet.) Dette gør det endnu nemmere at forenkle.

For eksempel,

\frac{\sqrt{144}}{\sqrt{36}}

${frac{{sqrt{144}}}{{sqrt{36}}}}$ kan omskrives som

\sqrt{\frac{144}{36}}

${sqrt{{frac{144}{36}}}}$ .

Billede med titlen Divide Square Roots Trin 3

3. Del rødderne. Divider tallene, som du ville gøre et hvilket som helst heltal. Sørg for at placere kvotienten under en ny radikal.

For eksempel,

\frac{144}{36} = 4

${frac{144}{36}}=4$ , Så

\sqrt{\frac{144}{36}} = \sqrt{4}

${sqrt{{frac{144}{36}}}}={sqrt{4}}$ .

Billede med titlen Divide Square Roots Trin 4

4. Forenkle, Hvis det er nødvendigt. Hvis rodtallet er et kvadrat, eller hvis en af faktorerne er et perfekt kvadrat, skal du forenkle udtrykket. Et kvadrat eller perfekt kvadrat er produktet af et heltal ganget med sig selv. For eksempel er 25 et perfekt kvadrat, fordi

5 \times 5 = 25

$5gange 5=25$ .

For eksempel er 4 et perfekt kvadrat, fordi

2 \times 2 = 4

$2gange 2=4$ . Dermed:

\sqrt{4}

${sqrt{4}}$

= \sqrt{2 \times 2}

$={sqrt{2 gange 2}}$

= 2

$=2$
så,

\frac{\sqrt{144}}{\sqrt{36}} = \sqrt{4} = 2

${frac{{sqrt{144}}}{{sqrt{36}}}}={sqrt{4}}=2$ .

Metode 2 af 4: Factoring rødder

Billede med titlen Divide Square Roots Trin 5

1. Udtryk problemet som en brøkdel. Udtrykket er formentlig allerede skrevet på denne måde. Hvis ikke, så skift det. At gøre det til en brøkdel gør de nødvendige trin nemmere at følge, især når man faktoriserer kvadratrødder. Husk, at et divisionstegn er det samme som en brøklinje.

For eksempel ved udregning $\sqrt{8} \div \sqrt{36}$ ${sqrt{8}}div {sqrt{36}}$ , omskriv udtrykket som: $\frac{\sqrt{8}}{\sqrt{36}}$ ${frac{{sqrt{8}}}{{sqrt{36}}}}$ .

Billede med titlen Divide Square Roots Trin 6

2. Faktor hver gulerod i faktorer. Faktor tallet som du ville gøre et helt tal. Lad faktorerne ligge under de radikale tegn.

For eksempel:

\frac{\sqrt{8}}{\sqrt{36}} = \frac{\sqrt{2 \times 2 \times 2}}{\sqrt{6 \times 6}}

${frac{{sqrt{8}}}{{sqrt{36}}}}={frac{{sqrt{2 gange 2 gange 2}}}{{sqrt{6 gange 6 }}}}$

Billede med titlen Divide Square Roots Trin 7

3. Forenkle brøkens tæller og nævner. Til for at forenkle en kvadratrod, ekskluderer du alle faktorer, hvoraf produktet er en firkant?. Et kvadrat er resultatet af et heltal ganget med sig selv. Faktoren bliver nu en koefficient uden for kvadratroden.

For eksempel:

\sqrt{} 2 \times 2 \times 2 \sqrt{6 \times 6}

${frac{{sqrt{{annuller{2gange 2gange }}2}}}{{sqrt{{annuller{6gange 6}}}}}}}$

2 \sqrt{2} 6

${frac{2{sqrt{2}}}{6}}$
så,

\frac{\sqrt{8}}{\sqrt{36}} = 2 \sqrt{2} 6

${frac{{sqrt{8}}}{{sqrt{36}}}}={frac{2{sqrt{2}}}{6}}$

Billede med titlen Divide Square Roots Trin 8

4. Fjern om nødvendigt det radikale tegn fra nævneren. Et udtryk kan som udgangspunkt ikke have en kvadratrod i nævneren. Hvis din brøk har en kvadratrod i nævneren, skal du eliminere den. Det betyder at fjerne roden i nævneren. For at gøre dette skal du gange tælleren og nævneren af brøken med kvadratroden, du skal eliminere.

Antag for eksempel, at dit udtryk er

6 \sqrt{2} \sqrt{3}

${frac{6{sqrt{2}}}{{sqrt{3}}}}$ , så skal du gange tæller og nævner med

\sqrt{3}

${sqrt{3}}$ for at fjerne kvadratroden fra nævneren:

6 \sqrt{2} \sqrt{3} \times \frac{\sqrt{3}}{\sqrt{3}}

${frac{6{sqrt{2}}}{{sqrt{3}}}}gange {frac{{sqrt{3}}}{{sqrt{3}}}}$

= 6 \sqrt{2} \times \sqrt{3} \sqrt{3} \times \sqrt{3}

$={frac{6{sqrt{2}}time {sqrt{3}}}{{sqrt{3}}time {sqrt{3}}}}$

= 6 \sqrt{6} \sqrt{9}

$={frac{6{sqrt{6}}}{{sqrt{9}}}}$

= 6 \sqrt{6} 3

$={frac{6{sqrt{6}}}{3}}$ .

Billede med titlen Divide Square Roots Trin 9

5. Forenkle yderligere, hvis det er nødvendigt. Nogle gange står man tilbage med koefficienter, der kan forenkles yderligere, eller reducere. Forenkle hele tallene i tælleren og nævneren ligesom du ville forenkle en brøk.

For eksempel,

\frac{2}{6}

${frac{2}{6}}$ kan reduceres til

\frac{1}{3}

${frac{1}{3}}$ , Så

2 \sqrt{2} 6

${frac{2{sqrt{2}}}{6}}$ kan reduceres til

1 \sqrt{2} 3

${frac{1{sqrt{2}}}{3}}$ , eller simpelthen

\frac{\sqrt{2}}{3}

${frac{{sqrt{2}}}{3}}$ .

Metode 3 af 4: Opdeling af kvadratrødder med koefficienter

Billede med titlen Divide Square Roots Trin 10

1. Forenkle koefficienterne. Det er tallene uden for det radikale. For at forenkle dem, del eller reducere, ignorere kvadratrødderne for nu.

Hvis du f.eks $4 \sqrt{32} 6 \sqrt{16}$ ${frac{4{sqrt{32}}}{6{sqrt{16}}}}$ skal regne, så forenkler du først $\frac{4}{6}$ ${frac{4}{6}}$ . Både tælleren og nævneren kan divideres med en faktor 2. Så du kan forenkle dette til: $\frac{4}{6} = \frac{2}{3}$ ${frac{4}{6}}={frac{2}{3}}$ .

Billede med titlen Divide Square Roots Trin 11

2. Forenkle kvadratrødderne. Hvis tælleren er delelig med nævneren, skal du blot dividere tallene under radikalerne. Hvis ikke, forenkle hver kvadratrod på samme måde som andre kvadratrødder.

For eksempel, da 32 er deleligt med 16, kan du dividere kvadratrødderne:

\sqrt{\frac{32}{16}} = \sqrt{2}

${sqrt{{frac{32}{16}}}}={sqrt{2}}$ .

Billede med titlen Divide Square Roots Trin 12

3. Multiplicer den/de forenklede koefficient(er) med den forenklede kvadratrod. Husk at der ikke kan være en kvadratrod i en nævner, så når du gange en brøk med en kvadratrod, sætter du kvadratroden i tælleren.

For eksempel,

\frac{2}{3} \times \sqrt{2} = 2 \sqrt{2} 3

${frac{2}{3}} gange {sqrt{2}}={frac{2{sqrt{2}}}{3}}$ .

Billede med titlen Divide Square Roots Trin 13

4. Fjern om nødvendigt kvadratroden i nævneren. Dette kaldes rationalisering af nævneren. Reglen er, at et udtryk ikke kan have en kvadratrod i nævneren. For at trække roden fra nævneren skal du gange tælleren og nævneren med den kvadratrod du vil trække fra.

For eksempel hvis du har et udtryk som

4 \sqrt{3} 2 \sqrt{7}

${frac{4{sqrt{3}}}{2{sqrt{7}}}}$ , så skal du gange tæller og nævner med

\sqrt{7}

${sqrt{7}}$ for at eliminere kvadratroden i nævneren:

4 \sqrt{3} \sqrt{7} \times \frac{\sqrt{7}}{\sqrt{7}}

${frac{4{sqrt{3}}}{{sqrt{7}}}} gange {frac{{sqrt{7}}}{{sqrt{7}}}}$

= 4 \sqrt{3} \times \sqrt{7} \sqrt{7} \times \sqrt{7}

$={frac{4{sqrt{3}} gange {sqrt{7}}}{{sqrt{7}} gange {sqrt{7}}}}$

= 4 \sqrt{21} \sqrt{49}

$={frac{4{sqrt{21}}}{{sqrt{49}}}}$

= 4 \sqrt{21} 7

$={frac{4{sqrt{21}}}{7}}$

Metode 4 af 4: At dividere med et binomium med en kvadratrod

Billede med titlen Divide Square Roots Trin 14

1. Bestem om du har et binomium i nævneren. Nævneren er tallet i den opgave, du dividerer med. Et binomium er et polynomium med to led. Denne metode gælder kun for division af kvadratrødder, der involverer et binomial.

Hvis du f.eks $1 5 + \sqrt{2}$ ${frac{1}{5+{sqrt{2}}}}$ Hvis du vil regne, har du et binomium i nævneren, fordi $5 + \sqrt{2}$ $5+{sqrt{2}}$ er et polynomium med to led.

Billede med titlen Divide Square Roots Trin 15

2. Bestem binomialets konjunktion. Konjugerede par er binomialer med de samme udtryk, men modsatte operatorer. Ved at bruge et konjunktivpar kan du fjerne kvadratroden fra nævneren.

For eksempel,

5 + \sqrt{2}

$5+{sqrt{2}}$ og

5 - \sqrt{2}

$5-{sqrt{2}}$ er konjunktive par, fordi de har de samme led, men modsatte operatorer.

Billede med titlen Divide Square Roots Trin 16

3. Gang tælleren og nævneren med konjunktionen af nævneren. Dette giver dig mulighed for at eliminere kvadratroden, fordi produktet af et konjugeret par er forskellen på kvadratet af hvert led i binomialet. Det er,

(-en - b) (-en + b) = -en 2 - b^{2}

$(a-b)(a+b)=a^{{2}}-b^{{2}}$ .

For eksempel:

1 5 + \sqrt{2}

${frac{1}{5+{sqrt{2}}}}$

= 1 (5 - \sqrt{2}) (5 + \sqrt{2}) (5 - \sqrt{2})

$={frac{1(5-{sqrt{2}})}{(5+{sqrt{2}})(5-{sqrt{2}})}}$

= 5 - \sqrt{2} (5 2 - (\sqrt{2})^{2}

$={frac{5-{sqrt{2}}}{(5^{{2}}-({sqrt{2}})^{{2}}}}$

= 5 + \sqrt{2} 25 - 2

$={frac{5+{sqrt{2}}}{25-2}}$

= 5 + \sqrt{2} 23

$={frac{5+{sqrt{2}}}{23}}$
dermed,

1 5 + \sqrt{2} = 5 + \sqrt{2} 23

${frac{1}{5+{sqrt{2}}}}={frac{5+{sqrt{2}}}{23}}$ .

Tips

Mange lommeregnere har specielle funktioner til brøker. Indtast koefficienten for tælleren, tryk på brøkknappen, og indtast derefter koefficienten for nævneren. Når du efterfølgende trykker på lighedstegnet, skulle lommeregneren have omskrevet koefficienterne i de mindste termer.
I modsætning til addition og subtraktion af rødder er det i en brøk ikke nødvendigt at forenkle rødderne først for at fjerne kvadraterne. Faktisk er det ofte bedre ikke at gøre dette.
Hvis du arbejder med kvadratrødder, er uægte brøker lettere at løse end blandede tal.

Advarsler

Sæt aldrig en decimal i en brøk. Det ville ellers være en brøkdel inden for en brøkdel.
Sæt aldrig et decimaltal eller et blandet tal foran en rod, konverter det til en brøk og forenkle hele udtrykket.
Efterlad aldrig en kvadratrod i nævneren af en brøk, men forenkle brøken.
Hvis nævneren indeholder en form for addition eller subtraktion, skal du bruge konjugeret parmetoden til at fjerne radikalet fra nævneren.

Artikler om emnet "Deler kvadratrødder"

Multiplicer kvadratrødder

Forenkle kvadratrødder

Tilføj og træk kvadratrødder fra

Løs kvadratrødder

Оцените, пожалуйста статью