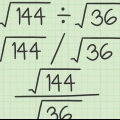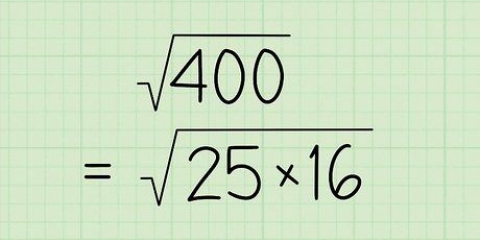Et andet eksempel: Vi vil finde kvadratroden af 25 (√(25)). Det betyder, at vi skal finde det tal, der ganget med sig selv har 25 som produkt. Da 5 = 5 × 5 = 25, kan vi sige, at √(25) = 5. Du kan også tænke på dette som at "fortryde" et kvadrat (eller potenstal). For eksempel, hvis vi ønsker at finde kvadratroden af 64 (√64), skal du betragte 64 som 8. først. Da en radikal i princippet `eliminerer` et kvadrat, kan vi sige, at √(64) = √(8) = 8. 
På den anden side kaldes tal, der ikke giver hele tal efter kvadratrod, ufuldkommen firkant. Når du tager kvadratroden af et af disse tal, får du normalt en decimal eller brøk. Nogle gange kan de involverede decimaler blive rigtig rodede. For eksempel, √(13) = 3.605551275464… 
1 = 1 × 1 = 1 2 = 2 × 2 = 4 3 = 3 × 3 = 9 4 = 4 × 4 = 16 5 = 5 × 5 = 25 6 = 6 × 6 = 36 7 = 7 × 7 = 49 8 = 8 × 8 = 64 9 = 9 × 9 = 81 10 = 10 × 10 = 100 11 = 11 × 11 = 121 12 = 12 × 12 = 144 
Antag, at du vil beregne kvadratroden af 900. Ved første øjekast ser det meget svært ud! Det er dog ikke svært, hvis vi faktor 900. `Faktorer` er de tal, der kan ganges sammen for at lave et andet tal. For eksempel, da 6 er produktet af 1 × 6 og 2 × 3, er faktorerne for 6 tallene 1, 2, 3 og 6. I stedet for at regne med tallet 900, hvilket er lidt ubelejligt, skriver vi det som 9 × 100. Nu, da 9 er et perfekt kvadrat og adskilt fra 100, kan vi tage dens kvadratrod. √(9 × 100) = √(9) × √(100) = 3 × √(100). Med andre ord, √(900) = 3√(100). Vi kan forenkle disse to trin yderligere ved at dividere 100 i faktorerne 25 og 4. √(100) = √(25 × 4) = √(25) × √(4) = 5 × 2 = 10. Så vi kan sige, at √(900) = 3(10) = 30. 
Bemærk: Selvom imaginære tal ikke kan repræsenteres med regulære tal, kan de stadig behandles som regulære tal på mange måder. For eksempel kan rødderne af negative tal kvadreres for at give disse negative tal ligesom enhver anden kvadratrod. For eksempel: i = -1. 

I vores eksempel deler vi 6,45 i par som dette: 6-,45-00. Bemærk, at der er et `resterende` nummer til venstre &mdash det er pointen. 
I vores eksempel er den første gruppe i 6-,45-00 6`eren. Det største tal mindre end eller lig med 6 er 2 — 2 = 4. Skriv et `2` over de 6 under radikalet. 
I vores eksempel starter vi med det dobbelte af 2, det første ciffer i vores svar. 2 × 2 = 4. Så trækker vi 4 fra 6 (vores første `gruppe`), og vi får 2 som svar. Så flytter vi den næste gruppe (45) ned en linje for at få 245. Til sidst skriver vi yderligere 4 til venstre, og efterlader lidt plads til at tilføje til sidst, sådan her: 4_. 
I vores eksempel leder vi efter tallet for at udfylde det tomme felt i 4_ × _; det gør svaret så stort som muligt, men stadig mindre end eller lig med 245. I dette tilfælde er svaret 5. 45 × 5 = 225, mens 46 × 6 = 276. 
Vi fortsætter med vores eksempel og fortsætter med 225 - 245 = 20. Så bringer vi det næste par cifre, 00, ned for at lave 2000. Hvis vi fordobler tallet over radikalet, får vi 25 × 2 = 50. Vi løser det ukendte i 50_ × _ =/< 2000, så får vi 3 som svar. På dette tidspunkt har vi `253` over det radikale - gentager vi dette igen, 9 er det næste ciffer. 
I vores eksempel er tallet under det radikale tegn 6,45, så vi flytter blot decimaltegnet op og placerer det mellem 2 og 5 af vores svar, hvilket giver os 2.539 udbytter. 

I vores eksempelopgave er et rimeligt skøn for kvadratroden af 40 måske 6.4, fordi vi fra ovenstående ved, at svaret nok er lidt tættere på 6 end på 7. 
Multiplicer 6,4 med sig selv, så 6,4 × 6,4 = 40,96, som er lidt større end det oprindelige antal. Derefter gange vi tallet med en tiendedel mindre end vores estimat ovenfor (fordi vores svar var for højt), og vi får 6,3 × 6,3 = 39,69. Dette er lidt lavere end vores oprindelige tal. Det betyder, at kvadratroden af 40 er et sted mellem 6,3 og 6,4 løgne. Fordi 39,69 er tættere på 40 end 40,96, ved du også, at kvadratroden er tættere på 6,3 end på 6,4. 
Lad os i vores eksempel vælge 6,33 til vores gæt med to decimaler. Kvadrat 6,33 og du får 6,33 × 6,33 = 40,0689. Da dette er lidt over vores oprindelige tal, vil vi prøve et lidt lavere tal, såsom 6,32. 6,32 × 6,32 = 39,9424. Dette er lidt under vores oprindelige tal, så vi ved, at den nøjagtige kvadratrod mellem 6.33 og 6.32 løgne. Hvis vi ville gå længere, kan vi fortsætte med at bruge samme tilgang for at få et svar, der er mere og mere præcist.
Løs kvadratrødder
Indhold
Selvom det skræmmende syn af et kvadratrodssymbol kan få folk med matematikangst til at ryste sig sammen, er kvadratrodsproblemer ikke så svære at løse, som de ser ud til ved første øjekast. Simple kvadratrodsopgaver kan ofte løses lige så nemt som simple multiplikations- og divisionsopgaver. Mere komplekse kvadratrodsproblemer kan på den anden side kræve lidt mere arbejde, men med den rigtige tilgang kan selv disse problemer let løses. Begynd at øve kvadratrodsproblemer i dag for at lære denne matematikfærdighed, som måske er ny for dig!
Trin
Del 1 af 3: Forstå kræfter og rødder

1. Kvaddre et tal ved at gange det med sig selv. For at forstå rødder er det bedst at starte med firkanterne. Kvadrater er nemme - at kvadrere et tal svarer til at gange det med sig selv. For eksempel: 3 i anden er det samme som 3 × 3 = 9, og 9 i anden er det samme som 9 × 9 = 81. Kvadrater er angivet med en lille "2" over og til højre for tallet i kvadrat - sådan her: 3, 9, 100 osv.
- Prøv selv at kvadrere nogle tal for at teste dette koncept. Husk, at det at kvadrere et tal ikke er andet end at gange det tal med sig selv. Du kan gøre dette selv med negative tal. I alle tilfælde vil svaret altid være positivt. For eksempel: -8 = -8 × -8 = 64.

2. For at finde roden af et tal skal du finde `det omvendte` af et kvadrat. Symbolet for kvadratroden (√, også kendt som det `radikale tegn`) er dybest set det `modsatte` af kvadratsymbolet (). Hvis du ser et radikalt tegn, kan du spørge dig selv: `Hvilket tal kan jeg gange med sig selv, så jeg får tallet under det radikale tegn??` For eksempel: hvis du ser kvadratroden √(9), så leder du efter tallet, der ganget med sig selv har ni som produkt. I dette tilfælde altså tre, fordi 3 = 9.

3. Kend forskellen mellem perfekte og uperfekte firkanter. Indtil nu var svarene på kvadratrodsproblemerne pæne, runde tal. Dette er ikke altid tilfældet - faktisk er der svar på kvadratrødder, der er meget lange, akavede decimaltal. Rodtal, der er hele tal (med andre ord tal, der ikke er brøker eller decimaler) kaldes firkanter. Alle ovenstående eksempler (9, 25 og 64) er kvadrater (også kaldet perfekte kvadrater), for ved at tage kvadratrødder får vi hele tal (3, 5 og 8) som et resultat.

4. Husk de første 10-12 firkanter. Som du sikkert har bemærket, er kvadratrødder eller kvadrater ofte meget nemme! Fordi disse matematiske problemer er så enkle, er det værd at bruge tid på at lære rødderne til de første 12 eller flere kvadrater. Du vil støde meget på disse tal, så du kan spare meget tid i det lange løb ved at lære dem tidligt. De første 12 felter er:

5. Forenkle rødder ved at fjerne firkanter, hvor det er muligt. Det kan nogle gange være vanskeligt at finde rødderne til ufuldkomne kvadrater - især hvis du ikke bruger en lommeregner (afsnittene nedenfor giver dig tricks til at gøre denne proces nemmere). Det er dog ofte muligt at forenkle tallene under det radikale tegn, for at gøre arbejdet med dem lettere. For at gøre dette skal du blot faktorisere tallet under radikalet, derefter tage kvadratroden af faktorer, der er kvadrater, og skrive svaret uden for radikalet. Dette er nemmere, end det lyder - læs videre for at lære mere!

6. Brug imaginære tal til rødderne af negative tal. Hvilken firkant er -16? Det er ikke 4 eller -4 — at kvadrere begge giver 16 (positivt). Ved du det ikke? Faktisk er der ingen måde at skrive kvadratroden af -16 eller et negativt tal med regulære tal. I disse tilfælde skal vi bruge imaginære tal (normalt i form af bogstaver eller symboler) til at erstatte kvadratroden af det negative tal. For eksempel bruges variablen `i` normalt til kvadratroden af -1. Som en generel regel vil kvadratroden af et negativt tal altid være et imaginært tal (eller indeholde et).
Del 2 af 3: Brug af lange divisionsalgoritmer

1. Bestil dit kvadratrodsproblem som lang division. Selvom det kan være lidt tidskrævende, er det muligt at beregne rødderne af vanskelige uperfekte kvadrater uden en lommeregner. For at gøre dette bruger vi en løsningsmetode (eller algoritme) som ligner - men ikke helt det samme som - en lang division.
- Skriv først kvadratroden ned på samme måde som lang division. Lad os f.eks. sige, at vi vil beregne kvadratroden af 6,45, hvilket bestemt ikke er et praktisk perfekt kvadrat. Først skriver vi et almindeligt radikalt symbol (√), derefter skriver vi tallet under det. Så trækker vi en streg over tallet, så det er i en lille `boks` - ligesom lang division. Da vi er færdige, noterede vi et aflangt `√` med 6,45 under.
- Vi skriver tal over problemet, så lad lidt plads.

2. Gruppér tallene i par. For at løse dit problem skal du gruppere cifrene i tallet under det radikale tegn i par, startende fra decimaltegnet. Du kan tilføje små highlights (såsom punktum, skråstreger, kommaer osv.) mellem dine par for at adskille dem.

3. Find det største tal, hvis kvadrat er mindre end eller lig med den første `gruppe`. Start med det første tal eller par til venstre. Vælg det største tal med et kvadrat, der er mindre end eller lig med `gruppen`. For eksempel, hvis gruppen er 37, ville du vælge de 6, fordi 6 = 36 (mindre end 37), men 7 = 49 (større end 37). Skriv dette tal over den første gruppe. Dette er det første ciffer i dit svar.

4. Dobbelt det tal, du lige har skrevet ned, skriv det under den første gruppe og træk det fra. Tag det første ciffer i dit svar (det tal, du lige har fundet), og fordoble det. Skriv dette under din første gruppe og træk det fra for at finde forskellen. Placer det næste par tal ved siden af svaret nedenfor. Skriv endelig det sidste ciffer af det dobbelte af det første ciffer i dit svar til venstre, og lad lidt plads ved siden af.

5. Udfyld den tomme plads. Dernæst er det meningen at tilføje et ciffer til højre for det tal, som du har skrevet til venstre. Vælg et tal, der ganges med dit nye tal, giver det størst mulige produkt, men alligevel er mindre end eller lig med det "trukne" tal. For eksempel, hvis dit `nedbragte` tal er 1700 og tallet til venstre er 40_, vil du udfylde det tomme felt med `404`, fordi 404 × 4 = 1616 (mindre end 1700), mens 405 × 5 = 2025. Nummeret, du finder i dette trin, er det andet ciffer i dit svar, så du kan tilføje det over radikalet.

6. Fortsæt med at bruge dine `blanke` tal til dit svar. Fortsæt med denne ændrede lange division, indtil du får nuller, når du trækker tallet fra `træk ned`, eller du har nået den ønskede nøjagtighed. Når du er færdig, er de tal, du brugte til at udfylde de tomme felter ved hvert trin (plus det allerførste tal, du brugte) cifrene i dit svar.

7. Flyt decimaltegnet for din oprindelige `divisor` op. For at runde dit svar af skal du sætte kommaet (decimaltegnet) på det rigtige sted. Heldigvis er dette nemt - alt du skal gøre er at justere det med decimaltegnet i dit originale tal. Hvis tallet under radikalen er 49,8, skal du flytte decimaltegnet op mellem de to tal over 9 og 8.
Del 3 af 3: Beregning af ufuldkomne firkanter hurtigt

1. Find ufuldkomne firkanter ved at estimere. Når du har lært dine firkanter udenad, bliver det meget nemmere at finde rødderne til ufuldkomne firkanter. Da du allerede kender et dusin kvadrater, kan ethvert tal, der falder mellem to af disse perfekte kvadrater, findes ved at estimere mellem disse værdier. For at starte skal du finde de to firkanter dit tal falder imellem. Bestem derefter, hvilken af disse to firkanter, der er tættest på tallet.
- Antag for eksempel, at vi skal finde kvadratroden af 40. Da vi har lært vores firkanter udenad, kan vi sige, at 40 falder mellem 6 og 7, eller 36 og 49. Da 40 er større end 6, vil dens kvadratrod være større end 6, og da den er mindre end 7, vil dens kvadratrod være mindre end 7. Tallet 40 er lidt tættere på 36 end 49, så svaret vil nok være lidt tættere på 6. I de næste trin vil vi gøre vores svar mere præcist.

2. Estimer kvadratroden til én decimal. Når du har valgt to felter, som dit tal ligger imellem, er det bare et spørgsmål om at estimere, indtil du finder et svar, du er tilfreds med. Jo længere du kommer, jo mere præcist er dit svar. For at starte skal du vælge en ti for dit svar - det behøver ikke at være korrekt, men du sparer tid, hvis du bruger sund fornuft ved at vælge et tal, der er tæt på det rigtige svar.

3. Gang skønnet med sig selv. Så kvadrerer du skønnet. Medmindre du er heldig, får du sandsynligvis ikke dit oprindelige nummer - du ender enten lidt højere eller lavere. Hvis dit svar er for højt, prøv igen med et lidt mindre skøn (og omvendt, hvis det er for lavt).

4. Fortsæt med at estimere, hvis det er nødvendigt. Hvis du er tilfreds med dine svar, vil du måske bare bruge et af dine første gæt. Men hvis du vil have et mere præcist svar, er alt hvad du skal gøre at vælge et estimat for din "hundrededel", der placerer dette estimat mellem dine to første. Hvis du fortsætter med dette mønster, kan du få et svar med tre, fire eller flere decimaler - det afhænger bare af, hvor langt du vil gå.
Tips
- For hurtige løsninger, brug en lommeregner. De fleste moderne regnemaskiner kan beregne kvadratrødder direkte. Normalt skal du blot indtaste dit nummer og derefter trykke på knappen med radikalen i anden potens (kvadratroden). For at finde kvadratroden af 841 skal du for eksempel trykke på følgende taster: 8, 4, 1, (√) og få det rigtigt 29 på som svar.
Artikler om emnet "Løs kvadratrødder"
Оцените, пожалуйста статью
Populær