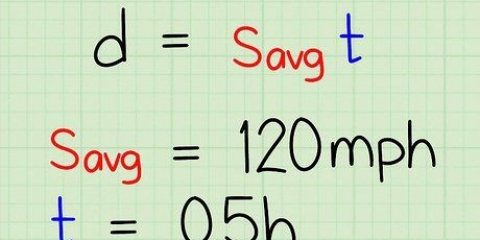I vores eksempel tager vi kvadratrødderne af 25 og 16. Se nedenunder: Sqrt(25×16) Sqrt(25) × Sqrt(16) 5 × 4 = 20 
Lad os tage kvadratroden af 147 som et eksempel. 147 er ikke produktet af to perfekte kvadrater, så vi kan ikke få en pæn heltalsværdi. Men det er produktet af et perfekt kvadrat og et andet tal - 49 og 3. Vi kan bruge disse oplysninger til at skrive vores svar i de enkleste vendinger: sqrt(147) = Sqrt(49 × 3) = Sqrt(49) × Sqrt(3) = 7 × Sqrt(3) 
Lad os vende tilbage til vores eksempel. Da 2 = 4 og 1 = 1, ved vi, at Sqrt(3) er mellem 1 og 2 - sandsynligvis tættere på 2 end 1. Vi vurderer, at 1,7. 7 × 1,7 = 11.9. Ved at tjekke dette med lommeregneren ser vi, at vi er ret tæt på svaret: 12.13. Dette virker også for de større tal. For eksempel er Sqrt(35) nogenlunde mellem 5 og 6 (sandsynligvis tættere på 6). 5 = 25 og 6 = 36. 35 er mellem 25 og 36, så kvadratroden vil være mellem 5 og 6. Da 35 er lige under 36, kan vi med en vis sikkerhed sige, at dens kvadratrod lige er lavere end 6. At tjekke med en lommeregner giver os et svar på omkring 5,92 - vi havde ret. 
Et eksempel: vi bestemmer kvadratroden af 45 ved hjælp af denne metode. Vi ved, at 45 = 9 × 5 og at 9 = 3 × 3. Så vi kan skrive kvadratroden sådan her: Sqrt(3 × 3 × 5). Bare fjern 3`erne og placer en 3`er uden for radikalen for at få en forenklet kvadratrod: (3)Sqrt(5). Nu kan du nemt vurdere. Et sidste eksempel; vi bestemmer kvadratroden af 88: sqrt(88) = Sqrt(2 × 44) = Sqrt(2 × 4 × 11) = Sqrt(2 × 2 × 2 × 11). Vi har flere 2`ere i vores kvadratrod. Da 2 er primtal, kan vi fjerne et par og placere en 2 uden for kvadratroden. = Vores kvadratrod i simpleste termer er (2) Sqrt(2 × 11) eller (2) Sqrt(2) Sqrt(11). Nu kan vi nærme os Sqrt(2) og Sqrt(11) og finde et estimeret svar, hvis vi ville. 

I vores eksempel er cifferet længst til venstre tallet 7. Fordi vi ved, at 2 = 4 7 < 3 = 9, kan vi sige, at n = 2, fordi det er det største heltal, hvis kvadrat er mindre end eller lig med 7. Skriv 2 i øverste højre kvadrant. Dette er det første ciffer i svaret. Skriv 4 (kvadraten af 2) i nederste højre kvadrant. Dette tal er vigtigt for det næste trin. 
I vores eksempel skriver vi en 4 under 7 og trækker den fra. Dette giver 3 som svar. 
I vores eksempel er følgende tal "80". Bemærk "80" ved siden af de 3 i venstre kvadrant. Gang derefter tallet øverst til højre med 2. Dette tal er 2, så 2 × 2 = 4. Bemærk "`4"` nederst til højre efterfulgt af _×_=. 
I vores eksempel udfylder vi 8, og det giver 4(8) × 8 = 48 × 8 = 384. Dette er mere end 380. Så 8 er for stort, men 7 er det nok ikke. Udfyld 7 og løs: 4(7) × 7 = 329. 7 er godt, fordi 329 er mindre end 380. Note 7 øverst til højre. Dette er det andet ciffer i kvadratroden af 780,14. 
I vores eksempel trækker vi 329 fra 380, og det giver 51 som resultat. 
I vores svar skriver vi nu et komma, fordi vi også støder på dette i 780.14. Flyt det næste par (14) ned i venstre kvadrant. 27 x 2 = 54, så vi skriver "54 _×_=" i nederste højre kvadrant. 
I vores eksempel er 549 × 9 = 4941, hvilket er mindre end eller lig med tallet til venstre (5114). 549 × 10 = 5490, hvilket er for højt, så 9 er vores svar. Skriv 9 som det næste tal øverst til højre og træk multiplikationsresultatet fra det venstre tal: 5114 -4941 = 173. 
Beregn kvadratroden af et tal uden en lommeregner
Indhold
Før lommeregneren kom, skulle både studerende og professorer beregne kvadratrødder med pen og papir. Forskellige teknikker er blevet udviklet på det tidspunkt til at tackle denne til tider tunge opgave, hvor nogle giver et groft skøn og andre beregner den nøjagtige værdi. Læs videre for at lære, hvordan du finder kvadratroden af et tal i nogle få nemme trin.
Trin
Metode 1 af 2: Rooting med primfaktorer

1. Opdel dit tal i firkanter. Denne metode bruger et tals faktorer til at finde kvadratroden af et tal (afhængigt af tallet kan dette være et nøjagtigt svar eller et skøn). Det faktorer af et givet tal er en tilfældig række af tal ganget sammen for at danne det pågældende tal. For eksempel kan du sige, at faktorerne 8 er lig med 2 og 4, fordi 2 × 4 = 8. Perfekte kvadrater er på den anden side heltal, der er produktet af andre heltal. For eksempel: 25, 36 og 49 er perfekte kvadrater, fordi de er lig med henholdsvis 5, 6 og 7. Anden potensfaktorer er, som du vil have forstået, faktorer, der også er perfekte kvadrater. For at finde en kvadratrod ved hjælp af primfaktorer, prøv først at dividere tallet i dets terningfaktorer.
- Tag følgende eksempel. Vi skal finde kvadratroden af 400. Til at begynde med deler vi tallet op i firkanter. Da 400 er et multiplum af 100, ved vi, at det er ligeligt deleligt med 25 - et perfekt kvadrat. Hurtig memorering fortæller os, at 400 / 25 = 16. 16 er tilfældigvis også en perfekt firkant. Så de kvadratiske faktorer på 400 er 25 og 16 fordi 25 × 16 = 400.
- Vi skriver dette som: Sqrt(400) = Sqrt(25 × 16)

2. Tag kvadratrødderne af dine kvadratrødder. Produktreglen for kvadratrødder siger, at for et givet tal -en og b, Sqrt(a × b) = Sqrt(a) × Sqrt(b). På grund af denne egenskab kan vi nu tage kvadratrødderne af terningfaktorerne og gange dem sammen for at få svaret.

3. Hvis dit nummer ikke kan indregnes helt perfekt, forenkle det. I virkeligheden vil de tal, du vil finde kvadratrødderne af, ikke være pæne afrundede tal med pæne kvadratrødder som 400. I disse tilfælde er det muligvis ikke muligt at få et heltal som svar. Ved at bruge alle de terninger, du kan finde, kan du i stedet bestemme svaret som en mindre, lettere at bruge kvadratrod. Det gør du ved at reducere tallet til en kombination af terningfaktorer og andre faktorer og derefter simplificere det.

4. Forenkle, hvis det er nødvendigt. Ved at bruge kvadratroden i de enkleste vendinger er det normalt ret nemt at få et groft skøn over svaret ved at estimere de resterende kvadratrødder og gange dem. En måde at forbedre dine gæt på er at finde de perfekte kvadrater på hver side af tallet i din kvadratrod. Du ved, at decimalværdien af tallet i din kvadratrod er et sted mellem disse to tal, så dit gæt bør også ligge mellem disse tal.

5. Alternativt kan du som et første skridt forenkle antallet tilmindste fælles multiplum. Søgningen efter kvadratfaktorer er ikke nødvendig, hvis du nemt kan finde primfaktorerne for et tal (faktorer, der også er primtal på samme tid). Skriv tallet i form af mindste fælles multipla. Søg derefter blandt dine faktorer efter tilsvarende par af primtal. Hvis du finder to primfaktorer, der matcher, skal du fjerne dem fra kvadratroden og sætte -en af disse tal uden for det radikale.
Metode 2 af 2: Find kvadratrødder uden lommeregner
Med en lang opdeling

1. Opdel cifrene i dit nummer i par. Denne metode ligner lang division, som giver dig mulighed for eksakt find kvadratroden af et tal ciffer for ciffer. Selvom det ikke er nødvendigt, kan opdeling af et tal i brugbare bidder gøre det lettere at løse, især hvis det er langt. Tegn først en lodret linje, der deler arbejdsområdet i 2 områder, derefter en kortere linje nær toppen af det højre område, og opdeler det i en mindre øvre del og en større del under. Opdel derefter tallet i talpar, startende fra decimalkommaet. Ifølge denne regel bliver 79520789182.47897 lig med "7 95 20 78 91 82,47 89 70". Skriv dette nummer i øverste venstre område.
- Lad os som et eksempel beregne kvadratroden af 780,14. Opdel dit arbejdsområde som angivet ovenfor og skriv ned "7 80, 14" i øverste venstre hjørne. Det er okay, hvis der kun er ét tal yderst til venstre i stedet for to. Du skriver så svaret (kvadratroden af 780,14) øverst i det højre område.

2. Find det største heltal n hvis kvadrat er mindre end eller lig med cifferet eller tallet længst til venstre. Find det største kvadrat, der er mindre end eller lig med dette tal, og find derefter kvadratroden af dette kvadrat. Dette nummer er n. Bemærk, at i det øverste højre område og skriv kvadratet af n i den nederste kvadrant af dette område.

3. Træk det tal fra, du har beregnet af cifferet eller tallet længst til venstre. Som med lang division er næste trin at trække kvadratet fra det tal, vi lige har brugt til at beregne. Skriv dette tal under tallet længst til venstre og træk dem fra hinanden. Skriv svaret nedenfor.

4. Flyt det næste tal ned. Placer dette ved siden af den værdi, du fandt i den forrige redigering. Gang tallet øverst til højre med to og skriv det ned nederst til højre. Spar plads ved siden af det tal, du lige har skrevet ned til multiplikationssummen, som du vil gøre i næste trin. Skriv her `"_×_="`.

5. Indtast tallene til højre. I det tomme rum af summen (til højre) skal du indtaste det største heltal, der vil gøre resultatet af multiplikationssummen til højre mindre end eller lig med det aktuelle tal til venstre.

6. Træk det tal, du lige har beregnet, fra det aktuelle tal til venstre. Så du trækker resultatet af multiplikationen til højre fra det aktuelle svar til venstre. Skriv dit svar direkte nedenfor.

7. Gentag trin 4. Flyt det næste par tal fra 780,14 ned. Hvis du kommer til et komma, så skriv det komma i svaret til højre. Gang derefter tallet øverst til højre med 2 og skriv svaret ud for ("_ × _") som ovenfor.

8. Gentag trin 5 og 6. Find det største tal, der giver et svar mindre end eller lig med det aktuelle tal til venstre. Løse.

9. For at gøre resultatet nøjagtigt, gentag den foregående procedure, indtil du finder svaret med det antal decimaler (hundrededele, tusindedele), du skal bruge.
Forstå proceduren
- Bemærk, at hvis du dividerer 88962 med 7 ved brug af lang division, er det første trin det samme: du har at gøre med det første ciffer af 88962 (8), og du vil have, at det største ciffer ganget med 7 skal være mindre end eller lig med 8. I bund og grund bestemmer du d så 7×d ≤ 8 < 7×(d+1). I dette tilfælde er d lig med 1.
- I vores eksempel (10A+B)² = L = S = 100A² + 2×10A×B + B². Husk at 10A+B repræsenterer vores svar L sammen med B i enhedspositionen og A i tierepositionen. For eksempel, hvis A=1 og B=2, så er 10A+B tallet 12. (10A+B)² er arealet af hele pladsen, mens 100A² er arealet af den største indre firkant, B² er arealet af mindste kvadrat og 10A×B er arealet af hver af de resterende rektangler. Gennem denne lange, komplicerede procedure kan vi finde arealet af hele firkanten ved at tilføje arealerne af de firkanter og rektangler, der udgør den.

1. Betragt det tal, hvis kvadratrod du vil beregne, som arealet S af et kvadrat. Da arealet af et kvadrat er L, hvor L er længden af en af dets sider, så ved at tage kvadratroden af dit tal, forsøger du at beregne længden L af siden af det kvadrat.

2. Giv hvert ciffer i dit svar et bogstav. Angiv variablen A som det første ciffer af L (kvadratroden, vi forsøger at beregne). B er det andet ciffer, C er det tredje, og så videre.

3. Giv et brev til hver "par tal" af det nummer du starter med. Giv variablen S-en til det første par cifre i S (startværdien), Sb til det andet cifrepar osv.

4. Forstå forholdet mellem denne metode og lang division. Denne metode til at finde en kvadratrod er i det væsentlige lang division, dividere startværdien med dens kvadratrod og tage kvadratroden som svaret "datum". Som med lang division, hvor du kun er interesseret i det næste ciffer ad gangen, er du kun interesseret i de næste to cifre ad gangen (som svarer til det næste ciffer i kvadratroden).

5. Find det største tal, hvis kvadrat er mindre end eller lig med S-en er. Det første ciffer A i vores svar er så det største heltal, hvis kvadrat ikke er større end S-en (A sådan, at A² ≤ Sa < (A+1)²). I vores eksempel er S-en = 7 og 2² ≤ 7 < 3², så A = 2.

6. Visualiser den firkant, du vil finde arealet af. Dit svar, kvadratroden af startværdien, er L, der beskriver længden af et kvadrat med areal S (startværdien). Værdierne for A, B og C repræsenterer tallene i værdien L. En anden måde at sige dette på er, at for et 2-cifret svar, 10A + B = L, og for et 3-cifret svar, 100A +10B + C = L, og så videre.

7. Træk A² fra S-en. Medbring et par tal (Sb) ned fra tallet S. s-en sb er næsten det samlede areal af kvadratet, hvorfra du lige har trukket arealet af det største indre kvadrat fra. Resten er sige tallet N1, som vi fik i trin 4 (N1 =380 i vores eksempel). N1 er lig med 2×10A×B + B² (arealet af de 2 rektangler plus arealet af det lille kvadrat).

8. Se på N1 = 2×10A×B + B², også skrevet som N1 = (2×10A + B) × B. I vores eksempel kender du allerede N1 (380) og A (2), så nu skal du finde B. B er sandsynligvis ikke et heltal, så du har brug for rent faktisk find det største heltal B, således at (2×10A + B) × B ≤ N1. Så nu har du: N1 < (2×10A + (B+1)) × (B+1).)

9. Løs ligningen. For at løse denne ligning skal du gange A med 2, flytte den til tiere (gang med 10), placere B i enhederne og gange resultatet med B. Med andre ord, (2×10A + B) × B. Det er præcis, hvad du gør, når du skriver "N_×_=" (med N=2×A) i nederste højre kvadrant i trin 4. I trin 5 bestemmer du det største heltal B, der passer under linjen, sådan at (2×10A + B) × B ≤ N1.

10. Træk arealet (2×10A + B) × B fra det samlede areal. Dette giver arealet S-(10A+B)², som du endnu ikke har taget højde for (og som du bruger til at beregne følgende tal på samme måde).

11. Gentag proceduren for at beregne det næste ciffer C. Flyt det næste par tal fra S og ned (Sc) for at få N2 til venstre, og se efter det største C, så du nu har: (2×10×(10A+B)+C) × C ≤ N2 (lig med to gange det tocifrede tal "A B" efterfulgt af "_×_=" . Bestem nu det største tal, du kan indtaste her, hvilket vil give dig et svar, der er mindre end eller lig med N2.
Tips
- Flytning af decimaltegnet to steder (en faktor 100) flytter decimaltegnet i den tilsvarende kvadratrod med ét sted (en faktor 10).
- I eksemplet kan 1,73 betragtes som "hvile": 780,14 = 27,9² + 1,73.
- Denne metode virker for ethvert talsystem, ikke kun decimalsystemet (ti decimaler).
- Læg gerne beregningerne, hvor du vil. Nogle mennesker skriver det over det tal, de vil beregne kvadratroden af.
- En alternativ metode er følgende: √z = √(x^2+y) = x + y/(2x + y/(2x + y/(2x) + ...))). For at beregne kvadratroden af 780,14, ville du tage det heltal i anden kvadrat tættest på 780,14 (28), så =780,14, x=28 og y=-3,86. Udfyldning og estimering giver os x + y/(2x), og dette giver (forenklede udtryk) 78207/2800 eller omkring 27.931(1); den næste periode, 4374188/156607 eller omkring 27.930986(5). Hver term tilføjer cirka 3 decimaler med præcision til den foregående.
Advarsler
- Sørg for at opdele tallet i par med udgangspunkt i decimalkommaet. Deling 79520789182.47897 som "79 52 07 89 18 2.4 78 97" giver et resultat, der ikke er korrekt.
Artikler om emnet "Beregn kvadratroden af et tal uden en lommeregner"
Оцените, пожалуйста статью
Populær