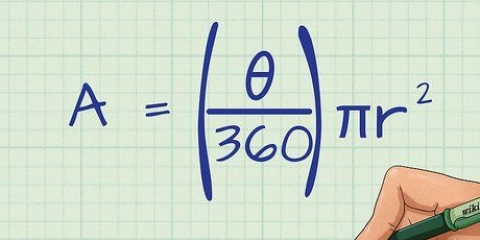For at finde s³ skal du gange s tre gange med sig selv: s³ = s x s x s 
Hvis du ikke er 100 % sikker på, om din form er en terning, mål alle sider for at se, om de er ens. Hvis de ikke er det, skal du bruge nedenstående metode til at beregne volumenet af en stråle. Bemærk: På prøvebillederne er målene angivet i tommer (in), men vi bruger centimeter (cm). 




Eksempel: Længden af denne bjælke er 4 cm, så l = 4 cm. Du skal ikke bekymre dig for meget om, hvilken side der er længden osv. Så længe du kun måler tre forskellige sider, bliver resultatet det samme. 
Eksempel: Bredden af denne bjælke er 3 cm, så b = 3 cm. Hvis du måler strålen med en lineal eller et målebånd, så glem ikke at skrive alt ned i samme måleenhed. 
Eksempel: Højden på denne stang er 6 cm, så h = 6 cm. 
I dette eksempel er l = 4, b = 3 og h = 6. Derfor er resultatet V = 4 x 3 x 6 = 72. 
For eksempel, hvis bjælkens dimensioner var i meter, ville du få l = 2 m, w = 4 m og h = 8 m. Volumen ville da være 2 m x 4 m x 8 m = 64 m³. 

I de fleste tilfælde er det tilstrækkeligt at afrunde pi til 3,14. Spørg din lærer, hvad han/hun vil have. Formlen for at finde volumenet af en cylinder er faktisk meget lig den for volumenet af en bjælke: du multiplicerer højden af formen med arealet af basen. For en bjælke er arealet af basen l x b, for en cylinder er det π x r², arealet af en cirkel med radius r. 

En anden mulighed er at måle omkredsen af cirklen (afstanden omkring den) med et stykke snor eller et målebånd. Indsæt derefter resultatet i denne formel: C (omkreds) er 2 x π x r. Divider omkredsen med 2 x π (6.28), og du har radius. For eksempel, hvis omkredsen du målte er 8 cm, så er radius 1,27 cm. Hvis du virkelig har brug for en nøjagtig måling, kan du bruge begge metoder til at se, om resultaterne er de samme. Hvis ikke, så tjek igen. Omkredsmetoden giver normalt et mere præcist resultat. 
Hvis radius er 4 cm, så er arealet af cirklen A = π x 4². 4² = 4 x 4 eller 16. 16 xπ = 16 x 3,14 = 50,24 cm². Hvis diameteren af basen er kendt, snarere end radius, skal du huske, at d = 2 x r. Så skal du dividere diameteren med to for at finde radius. 

V = π x 4² x 10 π x 4²= 50,24 50,24 x 10 = 502,4 V = 502,4 


Formlen for lige pyramider, hvor spidsen er direkte over midten af basen, er den samme som for skrå pyramider, hvor spidsen ikke er i midten. 
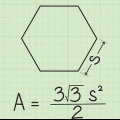
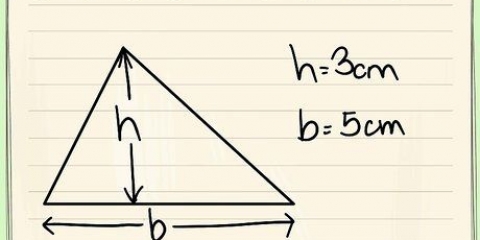
Formlen for arealet af en trekant er A = 1/2 x b x h, hvor b er basen og h er højden. Det er muligt at beregne arealet af enhver regulær polygon ved hjælp af formlen A = 1/2 xpxa, hvor A er arealet, p er omkredsen og a er apotemet, som er afstanden fra midten af formen til midten af en af siderne. Du kan også gøre det nemt for dig selv og bruge en online almindelig polygonberegner. 

Hvis vi havde haft en anden pyramide med en base med et areal på 26 og en højde på 8, ville resultatet have været: 1/3 x 26 x 8 = 69,33. 


Delen π x r² refererer til arealet af cirklen, der danner keglens bund. Så formlen for keglens rumfang er 1/3 x b x h, ligesom formlen for pyramiden i metoden ovenfor! 
I dette eksempel er radius 3 cm. Hvis vi sætter det i formlen får vi: A = π x 3². 3² = 3 x3 eller 9, så A = π x 9. A = 28,27 cm². 


I vores eksempel er det 141,35 x 1/3 = 47,12, keglens rumfang. Igen: 1/3 x π x 3² x 5 = 47,12. 




Hvis du for eksempel måler kuglen og ser, at omkredsen er 18 cm, skal du dividere det med 6,28, du ved, at radius er 2,87 cm. Det kan være vanskeligt at måle en kugle, så det er bedst at måle den tre gange og tage et gennemsnit (læg de tre mål sammen og divider med tre) for at få målingen så nøjagtig som muligt. For eksempel, hvis du målte tre gange, og resultaterne var 18 cm, 17,75 cm og 18,2 cm, skal du lægge det sammen (18 + 17,5 + 18,2 = 53,95) og dividere med 3 (53,95/3 = 17,98). Du bruger dette gennemsnit, når du beregner volumen. 


Så i vores eksempel bliver det 36 x 3,14 = 113,09. 
Beregn volumen
Indhold
- Trin
- Metode 1 af 6: Beregning af rumfanget af en terning
- Metode 2 af 6: Beregning af volumen af en stråle.
- Metode 3 af 6: Beregning af volumen af en cylinder
- Metode 4 af 6: Beregning af volumen af en almindelig pyramide
- Metode 5 af 6: Beregning af volumen af en kegle
- Metode 6 af 6: Beregning af volumen af en kugle
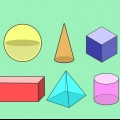
Volumenet af en figur er det tredimensionelle rum, figuren optager. Du kan repræsentere volumen som mængden af vand (eller luft, sand osv.).), der ville passe til formen, hvis den var helt fyldt. Almindeligt anvendte volumenmål er kubikcentimeter og kubikmeter.Denne artikel vil lære dig, hvordan du beregner volumen af seks forskellige tredimensionelle figurer, der almindeligvis stødes på i matematikprøver, inklusive terningen, kuglen og keglen. Du vil se, at der er mange ligheder, som vil gøre det nemt for dig at huske. Se om du kan finde de matcher!
Trin
Metode 1 af 6: Beregning af rumfanget af en terning

1. Genkend en terning. En terning er en tredimensionel form med seks identiske firkantede flader.Det er med andre ord en kasse med lige sider overalt.
- En terning er et godt eksempel på en terning, du kan have derhjemme. Sukkerterninger eller børneblokke er ofte også terninger.

2. Lær formlen til at beregne rumfanget af terningen. Da alle længderne af terningens sider har samme længde, er formlen til beregning af terningens rumfang meget let. Stedet, hvor to sider mødes, kaldes ribben. Vi forkorter volumen til "V". Ribbene, eller længden af siden, kalder vi her "s". Formlen bliver så V = s³

3. Find længden af den ene side af terningen. Afhængigt af opgaven kan denne information allerede være der, men du skal muligvis også selv måle den med en lineal. Husk, da det er en terning, skal alle længderne af siderne være lige store, så det er lige meget, hvilken du måler.

4. Sæt længden af siden i formlen V = s³ og beregn den. For eksempel, hvis du målte, at sidelængden af din terning er 5 cm, ville du skrive formlen som følger: V = (5)³. 5 x 5 x 5 = 125 cm³, så det er rumfanget af din terning!

5. Sørg for at skrive dit svar i kubikcentimeter. I eksemplet ovenfor blev terningen målt i centimeter, så svaret skal gives i kubikcentimeter. Hvis længden af terningens side havde været 3 meter, ville rumfanget have været V = (3 m)³ = 27 m³.
Metode 2 af 6: Beregning af volumen af en stråle.

1. Genkend en stråle. En bjælke er en figur, der består af seks rektangulære flader. Så det er faktisk et tredimensionelt rektangel, en slags kasse.
- Faktisk er en terning bare en speciel bjælke, hvor alle sider er lige store.

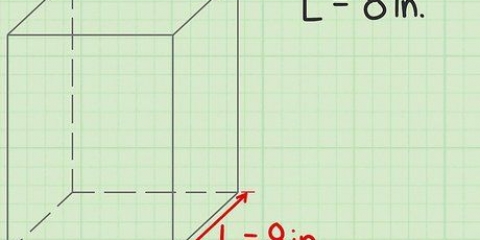
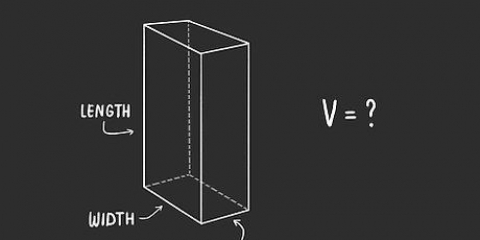
2. Lær formlen til at beregne volumenet af en stråle. Formlen for volumen af en bjælke er V = længde (l) x bredde (b) x højde (h), eller V = l x b x h. Bemærk: Billederne, der ledsager disse eksempler, viser "w" for bredden.

3. Find længden af bjælken. Længden er den længste side af bjælken, der er parallel med jorden eller overfladen, den hviler på. Længden kan allerede være angivet på billedet, eller du skal muligvis måle den med en lineal.

4. Find bredden af bjælken. Bjælkens bredde kan findes ved at måle den korte side, der er parallel med jorden eller overfladen, den hviler på. Tjek igen først om det allerede er angivet på billedet, og mål det ellers med din lineal.

5. Find bjælkens højde. Højde er afstanden fra jorden eller overfladen bjælken hviler på til toppen af bjælken. Se om det allerede er angivet på billedet og mål det anderledes med din lineal eller målebånd.

6. Indtast dimensionerne i formlen og beregn det. Husk at V = l x b x h.

7. Sørg for at skrive dit svar i kubikcentimeter. Resultatet er derfor 72 kubikcentimeter eller 72 cm³.
Metode 3 af 6: Beregning af volumen af en cylinder

1. Lær hvordan du identificerer en cylinder. En cylinder er en tredimensionel form med to identiske runde ender forbundet med en enkelt buet side. Det er faktisk en lige, rund stang.
- En dåse er et godt eksempel på en cylinder eller et AA-batteri.

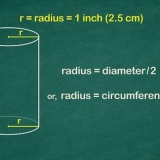
2. Husk formlen for volumen af en cylinder. For at beregne volumenet af en cylinder skal du kende dens højde og radius af dens cirkulære base.Radius er afstanden fra centrum af cirklen til kanten. Formlen er V =π x r² x h, hvor V er rumfanget, r er radius, h er højden, og π er konstanten pi.

3. Find basens radius. Hvis det allerede er angivet på billedet, skal du blot udfylde det. Hvis du fik diameteren i stedet for radius, skal du bare dividere den med 2 for at finde radius (d = 2 x r).

4. Mål formen, hvis radius ikke er angivet. Bemærk, at det kan være svært at måle den nøjagtige radius af en cirkel. En mulighed er at måle cirklen på det bredeste sted med din lineal fra top til bund, dividere det med to.

5. Beregn arealet af cirklen ved bunden. Indsæt radius i formlen π x r². Gang radius med sig selv, og gang resultatet med π. For eksempel:

6. Find højden på cylinderen. Dette er simpelthen afstanden mellem de to cirkulære baser eller afstanden fra overfladen, som cylinderen hviler på, til toppen af cylinderen. Se om længden allerede er angivet på billedet, eller mål den anderledes med din lineal eller målebånd.

7. Multiplicer arealet af basen med højden af cylinderen for at finde volumen. Indsæt værdierne i formlen V =π x r² x h. I vores eksempel med en radius på 4 cm og en højde på 10 cm:

8. Husk at skrive dit svar i kubikcentimeter. I dette eksempel blev cylinderen målt i centimeter, så svaret skal skrives i kubikcentimeter: V = 502,4cm³. Hvis cylinderen blev målt i meter, skulle volumen skrives i kvadratmeter (m³).
Metode 4 af 6: Beregning af volumen af en almindelig pyramide

1. Ved, hvad en almindelig pyramide er. En pyramide er en tredimensionel form med en polygon i bunden og siderne, der tilspidser til toppen (spidsen af pyramiden).En regulær pyramide er en pyramide, hvis basis er en regulær polygon, hvilket betyder, at alle sider og vinkler af denne polygon er lige store.
- Normalt er en pyramide afbildet med en firkantet base og sider, der tilspidser til et punkt, men bunden af en pyramide kan faktisk have 5, 6 eller 100 sider!
- En pyramide med en cirkel som sin base kaldes en kegle, som vi vil diskutere i den næste metode.

2. Lær formlen til at beregne volumen af den almindelige pyramide. Formlen for volumen af en regulær pyramide er V = 1/3 x b x h, hvor b er arealet af basen, og h er højden af pyramiden eller den lodrette afstand fra basen til toppen.

3. Beregn arealet af basen. Formlen for dette afhænger af antallet af sider af basen. I vores eksempel er basen en firkant med sider på 6 cm. Husk at formlen til at beregne arealet af et kvadrat er A = s². Så med vores pyramide er det 6 x 6 = 36 cm².

4. Find højden af pyramiden. I de fleste tilfælde vil det være angivet på billedet. I vores eksempel er pyramidens højde 10 cm.

5. Multiplicer arealet af bunden af pyramiden med højden, og divider med 3 for at finde volumen. Husk at formlen er V = 1/3 x b x h. I vores eksempel har pyramiden en base med et areal på 36 og en højde på 10, så rumfanget er 36 x 10 x 1/3 = 120.

6. Husk at skrive udfaldet i kubikenheder. Målene af pyramiden i eksemplet blev angivet i centimeter, så resultatet skal skrives i kubikcentimeter, 120 cm³. Hvis målene er angivet i meter, skriv svaret i kubikmeter (m³).
Metode 5 af 6: Beregning af volumen af en kegle

1. Lær hvad egenskaberne ved en kegle er. En kegle er en tredimensionel form med en cirkulær base og et enkelt punkt på den modsatte flade. En anden måde at se en kegle på er, at det er en speciel slags pyramide med en cirkulær base.
- Hvis spidsen af keglen er direkte over midten af basen, kaldes det en lige kegle. Hvis det ikke er direkte over midten, kaldes det en skrå kegle. Heldigvis er formlen til at beregne volumen den samme for begge typer kegler.

2. Kend formlen til beregning af keglens rumfang. Denne formel er V = 1/3 x π x r² x h, hvor r er radius af cirklen ved bunden, h er højden af keglen og π er konstanten pi, som kan afrundes til 3,14.

3. Beregn arealet af den cirkulære base af keglen. For at gøre dette skal du kende basens radius, som skal angives på dit billede. Hvis du fik diameteren i stedet for radius, skal du bare dividere det tal med 2, fordi diameteren er 2 gange radius (d = 2 x r). Indsæt derefter radius i formlen A = π x r² for at beregne arealet.

4. Find højden af keglen. Dette er den lodrette afstand fra bunden af keglen til toppen. I vores eksempel er højden af keglen 5 cm.

5. Multiplicer højden af keglen med arealet af basen. I vores eksempel er arealet af basen 28,27 cm² og højden er 5 cm, så b x h = 28,27 x 5 = 141,35.

6. Gang nu dette resultat med 1/3 (eller divider med 3) for at få keglens rumfang. I ovenstående trin beregnede vi faktisk volumenet af en cylinder, det vil sige en kegle, hvor væggene ville stå oprejst og ville ende i en anden cirkel. At dividere det med 3 giver dig volumen af keglen.

7. Husk at skrive udfaldet i kubikenheder. Vores kegle blev målt i centimeter, så volumenet skal udtrykkes i kubikcentimeter: 47,12 cm³.
Metode 6 af 6: Beregning af volumen af en kugle

1. Genkend en kugle. En kugle er en perfekt rund tredimensionel form, hvor hvert punkt på dens overflade er lige langt fra midten. Det er med andre ord en bold.

2. Lær formlen til at beregne rumfanget af en kugle. Formlen er V = 4/3 x π x r³ (dvs.: "fire tredjedele pi gange kubik r"), hvor r er kuglens radius, og π er konstanten pi (3.14).

3. Find kuglens radius. Hvis radius allerede er angivet på billedet, er det nemt. Givet diameteren, divider dette tal med 2 for at få radius. Kuglens radius i dette eksempel er 3 centimeter.

4. Mål kuglen, hvis radius ikke er angivet. Hvis du skal måle en kugle (såsom en tennisbold) for at finde radius, skal du finde en streng, der er lang nok til at vikle hele vejen rundt om den. Vikl den derefter rundt om objektet på det bredeste sted, og markér det punkt, hvor strengen forbindes igen. Mål derefter denne del af snoren med en lineal for at kende kuglens omkreds. Divider det med 2 x π eller 6,28, så kender du radius.

5. Hæv radius til tredje potens for at finde r³. At hæve til tredje potens betyder simpelthen at gange tallet tre gange med sig selv, så r³ = r x r x r. I vores eksempel bliver r=3 3 x 3 x 3 = 27.

6. Gang dit svar med 4/3. Du kan gøre det med en lommeregner, eller bare gøre det selv og forenkle brøken. I vores eksempel er det 27 x 4/3 = 180/3 eller 36.

7. Multiplicer resultatet med π for at finde kuglens rumfang. Det sidste trin i beregningen af volumen er at gange resultatet indtil videre med π. Afrund π til to decimaler, det er nok til de fleste matematikopgaver (medmindre din lærer siger andet), så gang det med 3,14 og du har fået dit svar.

8. Skriv dit svar i kubikenheder. I vores eksempel målte vi i centimeter, så svaret er V = 113,09 cm³.
Artikler om emnet "Beregn volumen"
Оцените, пожалуйста статью
Populær