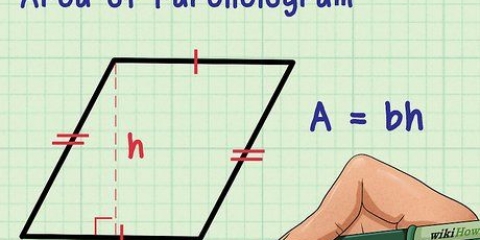Gratis trin for trin instruktioner 
Område = 1/2 x (3 cm x 5 cm) 
Område = 1/2 x (3 cm x 5 cm) Overflade = 1/2 x 15 cm Areal = 7.5 cm 
Areal = √{6 (6 - 3)(6 - 4)(6 - 5)} 
6 - 3 = 3 6 - 4 = 2 6 - 5 = 1 Areal = √{6 (3)(2)(1)} 
Areal = 1/2(b)(c) x sin A Areal = 1/2(150)(231) x sin A 
Areal = 1/2(150)(231) x sin A Areal = 1/2(34.650) x sin A Areal = 17.325 x sin A Areal = 17.325 x .8386705 Areal = 14.530 cm
Beregn arealet af en trekant
Indhold
Selvom den mest almindelige metode til at beregne arealet af en trekant er at gange dens halve base med dens højde, er der en række andre måder at beregne arealet af en trekant på, afhængigt af de tilgængelige data. Dette inkluderer længden af alle tre sider, længden af den ene side af en ligesidet trekant og længden af to sider sammen med den inkluderede vinkel. Læs her, hvordan du kan beregne arealet af en trekant ved hjælp af disse data.
Trin
Metode 1 af 4: Med basen og højden
1. Bestem bunden og højden af din trekant. Basen af trekanten er længden af den ene side, som normalt er den nederste side af trekanten. Højde er længden fra bunden til det øverste hjørne af trekanten, som er vinkelret på bunden. I en retvinklet trekant er bunden og højden de to sider, der mødes i en 90 graders vinkel. Men i en anden trekant, som det ses nedenfor, vil højdelinjen skære lige igennem formen.
- Når du har bestemt trekantens base og højde, er du klar til at begynde at bruge formlen.
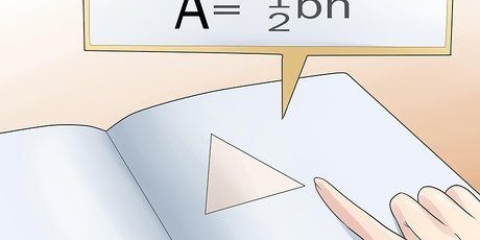
2. Skriv formlen ned for at finde arealet af en trekant. Formlen for denne type problemer er Areal = 1/2 (basis x højde), eller 1/2 (bh). Når du har noteret det hele, kan du begynde at udfylde længden af højden og bunden.
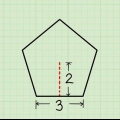
3. Indtast basis- og højdeværdier. Find trekantens base og højde og brug disse værdier i ligningen. I dette eksempel er trekantens højde 3 cm, og trekantens bund er 5 cm. Sådan ser formlen ud efter at have indtastet disse værdier:
4. Løs ligningen. Du kan gange højden gange basen først, fordi disse værdier er i parentes. Så gange du resultatet med 1/2. Husk, at du vil give svaret i kvadratmeter, fordi du arbejder i todimensionelt rum. Sådan løses dette til det endelige svar:
Metode 2 af 4: Brug af længden af hver side (Heron`s Formula)
1. Beregn trekantens halve omkreds (semiperimeter). For at finde trekantens halve omkreds skal du bare lægge alle siderne sammen og dividere resultatet med to. Formlen for at finde den halve omkreds af en trekant er som følger: semiperimeter = (længde af side a + længde af side b + længde af side c) / 2, eller s = (a + b + c) / 2. Da alle tre længder af den retvinklede trekant er givet, 3 cm, 4 cm og 5 cm, kan du sætte disse direkte ind i formlerne og løse problemet for den halve omkreds:
- s = (3 + 4 + 5)/2
- s = 12/2
- s = 6
2. Indtast de korrekte værdier i formlen for at finde arealet af en trekant. Denne formel til at finde arealet af en trekant kaldes også Herons formel og lyder sådan her: Areal = √{s (s - a)(s - b)(s - c)}. Vi gentager det forrige trin hvor s den halve omkreds er og -en, b, og c trekantens tre sider. Gør brug af følgende rækkefølge af operationer: start med at løse alt inden for parentesen, derefter alt under det radikale tegn og til sidst selve kvadratroden. Sådan ser denne formel ud, når du har indtastet alle kendte værdier:
3. Træk værdierne fra inden for parentes. Altså: 6 - 3, 6 - 4 og 6 - 5. Her er resultatet på papir:
4. Multiplicer resultaterne af disse operationer. Gang 3 x 2 x 1 for at få 6 som svar. Du skal gange disse tal sammen, før du gange dem med 6, fordi de står i parentes.
5. Gang det foregående resultat med halvdelen af omkredsen. Gang derefter resultatet, 6, med den halve omkreds, som også er 6. 6 x 6 = 36.
6. Beregn kvadratroden. 36 er et perfekt kvadrat og √36 = 6. Glem ikke den enhed, du startede med -- centimeter. Udtryk det endelige svar i kvadratcentimeter. Arealet af trekanten med siderne 3, 4 og 5 er 6 cm.
Metode 3 af 4: Brug af den ene side af en rektangulær trekant
1. Find siden af den ligesidede trekant. En ligesidet trekant har sider af lige længde og lige vinkler. Du ved, at du har at gøre med en ligesidet trekant, enten fordi dette er en given ting, eller fordi du ved, at alle vinkler og alle sider har samme værdi. Værdien af en af siderne i denne trekant er 6 cm. Bemærk dette.
- Hvis du ved, du har at gøre med en ligesidet trekant, men kun omkredsen er kendt, skal du bare dividere denne værdi med 3. For eksempel er længden af den ene side af en ligesidet trekant med omkreds 9 meget enkelt 9/3 eller 3.
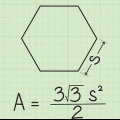
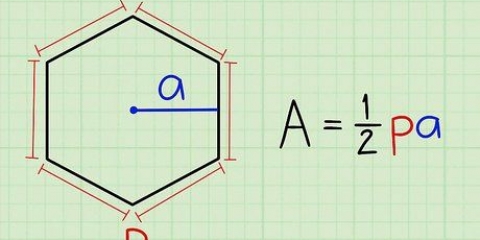
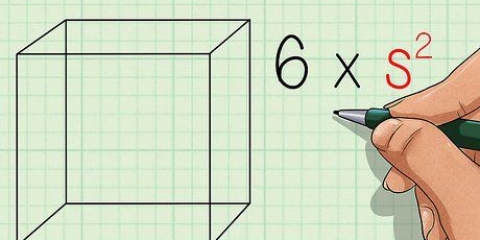
2. Skriv formlen ned for at finde arealet af en ligesidet trekant. Formlen for denne type problemer er areal = (s^2)(√3)/4. Noter det s "silke" betyder.
3. Anvend værdien af en side på ligningen. Beregn først kvadratet på siden med værdien 6 for at få 36. Find derefter værdien af √3, hvis svaret skal angives i decimaler. Indtast nu √3 i din lommeregner for at få 1.732 at få. Divider dette tal med 4. Bemærk, at du også kan dividere 36 med 4 og derefter gange med √3 -- rækkefølgen af operationer har ingen indflydelse på svaret.
4. Løse. Nu handler det primært om bare at tælle. 36 x √3/4 = 36 x .433 = 15.59 cm Arealet af en ligesidet trekant med en side på 6 cm er 15.59 cm.
Metode 4 af 4: Brug af længden af to sider og den inkluderede vinkel
1. Find værdien af længderne af to sider og den inkluderede vinkel. Den inkluderede vinkel er vinklen mellem trekantens to kendte sider. Du skal kende disse værdier for at finde arealet af en trekant ved hjælp af denne metode. Lad os antage en trekant med følgende dimensioner:
- vinkel A = 123º
- side b = 150 cm
- side c = 231 cm
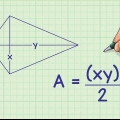
2. Skriv formlen ned for at finde arealet af trekanten. Formlen for at finde arealet af en trekant med to kendte sider og en kendt inkluderet vinkel er som følger: Areal = 1/2(b)(c) x sin A. I denne ligning repræsentere "b" og "c" sidernes længder og "-en" hjørnet. Du skal altid tage vinklens sinus i denne ligning.
3. Udfyld værdierne i ligningen. Sådan ser ligningen ud, når du har indtastet disse værdier:
4. Løse. For at løse denne ligning skal du først gange siderne og dividere resultatet med to. Derefter ganges dette resultat med sinus af vinklen. Værdien af sinus kan findes med din lommeregner. Glem ikke at give dit svar i kubikenheder. Sådan gør du det:
Tips
- Hvis du ikke forstår, hvorfor den grundlæggende højdeformel fungerer på denne måde, er her en kort forklaring. Hvis du laver en anden, identisk trekant og sætter den ved siden af hinanden, danner den enten et rektangel (to rette trekanter) eller et parallelogram (to ikke-retvinklede trekanter). For at finde arealet af et rektangel eller et parallelogram skal du blot gange basen med højden. Da en trekant er lig med et halvt rektangel eller parallelogram, følger det, at arealet af en trekant er lig med en halv base gange dens højde.
Artikler om emnet "Beregn arealet af en trekant"
Оцените, пожалуйста статью
Populær
