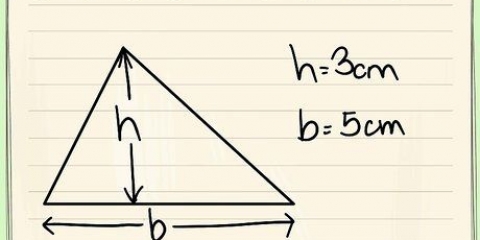
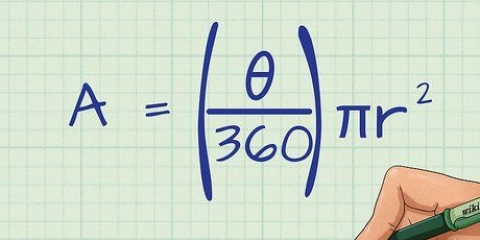I vores eksempel er trekantens areal=½ x 3 x 2=3. 
I vores eksempel er A(total af femkanten)=5 x A(trekant)=5 x 3=15. 



Det grundlag af trekanten er ½ gange siden af femkanten. I vores eksempel er dette ½ x 7=3,5 enheder. Det hjørne i midten af femkanten er altid 36º. (Forudsat 360º for en hel cirkel, kan du opdele dette i 10 mindre trekanter. 360 ÷ 10=36, så vinklen på en sådan trekant er 36º). 
I en retvinklet trekant er er tangent af en vinkel lig med længden af den modsatte side divideret med længden af den tilstødende side. Siden modsat vinklen på 36º er trekantens base (halve side af femkanten). Den tilstødende side af vinklen på 36º er højden af trekanten. tan(36º)=modsat / tilstødende I vores eksempel er tan(36º)=3,5 / højde højde x tan(36º)=3,5 højde=3,5 / tan(36º) højde = (ca.) 4.8. 
I vores eksempel er arealet af en af de små trekanter=½bh=½(3.5)(4.8)=8.4. 
I vores eksempel er arealet af hele femkanten=8,4 x 10=84. 

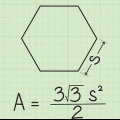
Arealet af en regulær femkant=(5s ) / (4tan(36º)), hvor s=længde af den ene side. tan(36º)=√(5-2√5). Hvis din lommeregner ikke har en `tan`-funktion, skal du bruge formlen for arealet: Area=(5s) / (4√(5-2√5)). 
Arealet af en regulær femkant=(5/2)rsin(72º), hvor r radius er.
Beregn arealet af en femkant
Indhold
En femkant er en polygon med fem lige sider. Næsten alle problemer, du vil støde på i matematiktimerne, vil involvere regulære femkanter med fem lige sider. Der er to almindelige måder at beregne arealet på, alt efter hvor meget information du har.
Trin
Metode 1 af 3: Bestemmelse af arealet ved hjælp af siderne og apotemet

1. Start med længden af siden og apotem. Denne metode virker for almindelige femkanter med fem lige sider. Ud over længden af siden har du brug for femkantens `apothema`. Apotemet er linjen fra midten af femkanten til en side, som skærer siden vinkelret (dvs. i en vinkel på 90º).
- Forveksle ikke apotemet med radius af en polygon, fordi den skærer en vinkel (toppunkt) i stedet for et punkt i midten af siden. Hvis du kun kender længden af en side og radius, fortsæt til næste metode.
- Som eksempel bruger vi en femkant med side 3 og apotem 2.

2. Del femkanten i fem trekanter. Tegn fem linjer fra midten af femkanten, som hver fører til et toppunkt (hjørne). Du har nu fem trekanter.

3. Beregn arealet af en trekant. Hver trekant har en grundlag lig med siden af femkanten. Den har også en højde som er lig med apotemet. (Husk, højden af en trekant er længden af den side, der er vinkelret på dens basis og strækker sig til et toppunkt). For at beregne arealet af en trekant bruger du ½ x basis x højde.

4. Multiplicer med fem for det samlede areal af femkanten. Vi har opdelt femkanten i fem lige store trekanter. For at beregne det samlede areal skal du gange arealet af en trekant med fem.
Metode 2 af 3: Bestemmelse af arealet ved hjælp af længden af en side

1. Start med længden af den ene side. Denne metode virker kun for almindelige femkanter, som har fem sider af lige længde.
- I dette eksempel bruger vi en femkant med længde 7 for hver side.

2. Del femkanten i fem trekanter. Tegn en linje fra midten af femkanten til et toppunkt. Gentag for hvert toppunkt. Du har nu fem trekanter, hver af samme størrelse.

3. Del en trekant i to. Tegn en linje fra midten af femkanten til bunden af en trekant. Denne linje skal skære basen i en ret vinkel (90º), som deler trekanten i to lige store, mindre trekanter.

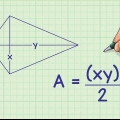
4. Mærk en af de mindre trekanter. Vi kan allerede mærke en side og en vinkel i den mindre trekant:

5. Beregn højden af trekanten. Det højde af denne trekant er siden vinkelret på den side af femkanten, der fører til midten. Vi bruger simpel trigonometri til at bestemme længden af denne side:

6.Beregn arealet af trekanten. Arealet af en trekant er lig med ½ base x højde. (A=½bh.) Nu hvor du kender højden, skal du indtaste disse værdier for at bestemme højden på din lille trekant.

7. Multiplicer for at finde området af femkanten. En af disse mindre trekanter dækker 1/10 af femkantens areal. For det samlede areal skal du gange arealet af den mindre trekant med 10.
Metode 3 af 3: Brug af en formel

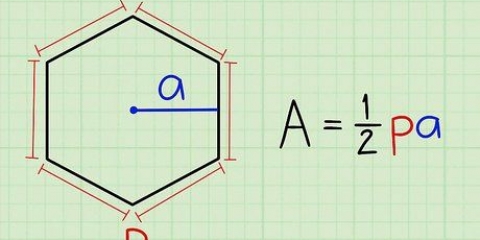
1. Brug omridset og apotem. Apotemet er en linje fra midten af en femkant, der skærer den ene side i en ret vinkel. Hvis længden er angivet, så kan du bruge denne simple formel.
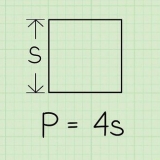
- Arealet af en regulær femkant =far / 2, hvor s=omkredsen og -en=apotemet.
- Hvis du ikke kender omkredsen, udregn den ved hjælp af længden af siden: p=5s, hvor s er længden af siden.

2. Brug længden af siden. Hvis du kun kender længden af siderne, skal du bruge følgende formel:

3. Vælg en formel, der kun bruger radius. Du kan endda finde området, hvis du kun kender radius. Brug følgende formel:
Tips
- Uregelmæssige femkanter eller femkanter med ulige sider er sværere at studere. Den bedste fremgangsmåde er normalt at opdele femkanten i trekanter og lægge arealer af alle trekanter sammen. Du skal muligvis også tegne en større form rundt om femkanten, beregne dens areal og derefter trække arealet af det ekstra rum.
- Hvis det er muligt, så brug både en geometrisk metode og en formel, og sammenlign resultaterne for at kontrollere dit svar. Svarene kan afvige en smule, hvis du udfylder formlen fuldstændigt på én gang (fordi så mangler de trin, du gennemfører i), men de burde ligge meget tæt på hinanden.
- Eksemplerne givet her bruger afrundede værdier for at gøre deres matematik lettere. Hvis du har en rigtig polygon med de givne sidelængder, får du lidt anderledes resultater for de øvrige længder og areal.
- Formlerne er afledt af geometriske metoder, svarende til dem, der er beskrevet her. Prøv selv at finde ud af, hvordan du kan distrahere dem. Radiusformlen er sværere at udlede end de andre (tip: du har brug for dobbeltvinklet identitet).
Artikler om emnet "Beregn arealet af en femkant"
Оцените, пожалуйста статью
Populær