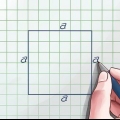
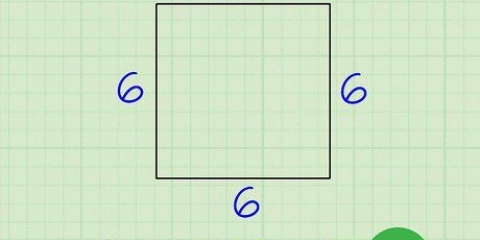
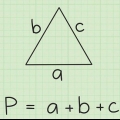Hvis firkanten har en side af længden 4:Omkreds = 4 * 4, med andre ord 16. Hvis firkanten har en side med længden 6: Omkreds = 4 * 6, med andre ord 24. 

Hvis arealet af kvadratet er 20, så er længden af siden s: =√20 eller 4.472 Hvis arealet af kvadratet er 25, så er længden af siden s = √25 eller 5. 
For et kvadrat med et areal på 20 og en sidelængde på 4.473 er omkredsen: Omkreds = 4 * 4,472 eller 17.888. For en firkant med et areal på 25 og en sidelængde på 5 er omkredsen: Omkreds = 4 * 5 eller 20. 


a + a = (2r), nu kan vi forenkle: 2a = 4(r), divider nu begge sider med 2: (a) = 2(r), tag nu kvadratroden af hver side: a = √(2)r.Vores længde på en side s af det indskrevne kvadrat = √(2)r. 

Bemærk: du kunne også have gjort det på denne måde: gange radius (10) med tallet 5.567. 10*5.567 = 56.57, men fordi det kan være svært at huske, må du hellere gennemgå hele processen.
Beregning af omkredsen af et kvadrat
Indhold
Omkredsen af en todimensionel figur er den samlede afstand omkring figuren eller summen af længderne af siderne. Definitionen af et kvadrat er en figur med fire lige store sider og fire rette vinkler (90°) mellem disse sider. Da alle sider har samme længde, er det meget nemt at bestemme omkredsen af en firkant! Denne artikel dækker først, hvordan man beregner omkredsen af et kvadrat, hvis du kender længden af en af dets sider. Så viser vi dig, hvordan du beregner omkredsen, hvis du kun kender arealet, og i sidste afsnit lærer vi dig, hvordan du beregner omkredsen af et indskrevet kvadrat i en cirkel, hvis radiuslængde er kendt.
Trin
Metode 1 af 3: Find omkredsen af en firkant, hvis du kender længden af en side

1. Tænk på formlen for omkredsen af et kvadrat. For en firkant, hvor vi finder længden af siden s omkredsen er simpelthen fire gange længden af den side: Omkreds = 4s (bemærk: på billederne bruges bogstavet P til omrids, fra den engelske `perimeter`).

2. Find længden af en side og gang den med 4 for at finde omkredsen. Afhængigt af opgaven skal du muligvis måle med en lineal eller se på andre oplysninger for at bestemme længden af en side. Her er nogle eksempler på omkredsberegninger:
Metode 2 af 3: Bestemmelse af omkredsen af en firkant, hvis du kender dens areal

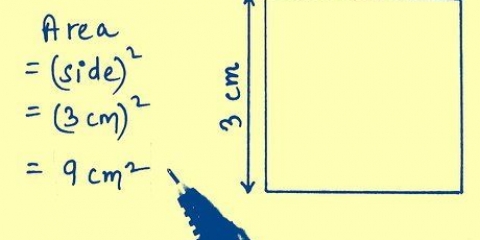
1. Kend formlen for arealet af en firkant. Arealet af ethvert rektangel (husk at kvadrater er specielle rektangler) kan defineres som basis gange højde.Da base og højde er ens i tilfælde af en firkant, er arealet af en firkant med side s: s*s. Med andre ord: areal = s.

2. Tag kvadratroden af området. Kvadratroden af området giver dig længden af en af kvadratets sider. For de fleste tal skal du bruge en lommeregner til at beregne kvadratroden. Indtast tallet først, og tryk derefter på kvadratroden (√).

3. Gang længden af siden med 4 for at finde omkredsen. Brug den sidelængdeværdi, du lige har fundet i formlen Omkreds = 4s. Resultatet er omkredsen af dit kvadrat!
Metode 3 af 3: Beregning af omkredsen af et indskrevet kvadrat i en cirkel, hvis du kender radius

1. Forstå, hvad en indskrevet firkant er. En indskrevet firkant i en cirkel er en firkant tegnet i en cirkel, hvor alle hjørner af firkanten rører cirklen.

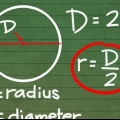
2. Forstå sammenhængen mellem radius af cirklen og længden af kvadratets sider. Afstanden fra midten af en indskrevet firkant til ethvert hjørne er lig med radius af cirklen. Til sidelængden s for at finde, skal vi først forestille os, at vi skærer firkanten i halve diagonalt, så der dannes to ligesidede trekanter. Disse trekanter har lige store sider -en og b og en hypotenuse c, som vi ved er lig med to gange cirklens radius, dvs 2r.

3. Brug Pythagoras sætning til at finde længden af kvadratets side. Pythagoras sætning er som følger: i en retvinklet trekant er summen af kvadraterne af længderne af de rektangulære sider (a,b) lig med kvadratet på hypotenusens længde (c), a + b = c. Fordi sider -en og b er lige store (vi har stadig at gøre med et kvadrat!) og det ved vi c=2r vi kan nu skrive ligningen ud og forenkle den for at finde længden af en side:

4. Multiplicer længden af den ene side af kvadratet med fire for at finde omkredsen. I dette tilfælde er omkredsen af firkanten: Omkreds = 4√(2)r. Omkredsen af et indskrevet kvadrat i en cirkel er derfor altid lig med 4√(2)r, eller omkring 5,657r

5. Løs et eksempelspørgsmål. Vi tager et indskrevet kvadrat i en cirkel med en radius på 10. Det betyder kvadratets diagonal = 2(10) eller 20. Pythagoras sætning lærer os at: 2(a) = 20, Så 2a = 400. Divider nu begge sider med to, det ser vi a = 200. Tag kvadratroden af hver side, og vi ser det a = 14,142. Multiplicer dette med 4 for at finde omkredsen af dit kvadrat: Omkreds = 56,57.
Artikler om emnet "Beregning af omkredsen af et kvadrat"
Оцените, пожалуйста статью
Populær