For eksempel, hvis rumfanget af prismet er 64  ), vil din formel se sådan ud:
), vil din formel se sådan ud:


For eksempel, hvis basen er et rektangel, der er 8 meter langt og 2 meter bredt, vil du beregne arealet som følger:



For eksempel, hvis du har beregnet, at arealet af basen er 16 m, vil din formel se sådan ud:


For eksempel i ligningen  , du skal dividere hver side med 16 om
, du skal dividere hver side med 16 om  at beregne. Dermed:
at beregne. Dermed:


Så højden af det rektangulære prisme er 4 meter. 

For eksempel, hvis du ved, at rumfanget af prismet er 840 kubikmeter ( ), vil din formel se sådan ud:
), vil din formel se sådan ud:


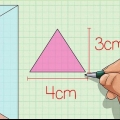
Hvis du kender længden af alle tre sider af en trekant, kan du beregne arealet ved hjælp af Herons formel.Læs Beregn arealet af en trekant for detaljerede instruktioner. For eksempel, hvis trekantens basis er 12 meter, og trekantens højde er 7 meter, så find arealet som følger:




For eksempel, hvis du ved, at arealet af basen er 42 m2, vil din formel se sådan ud:


For eksempel i ligningen  , du skal dividere hver side med 42 for at bestemme
, du skal dividere hver side med 42 for at bestemme  . Dermed:
. Dermed:


Så højden af dit trekantede prisme er 20 meter. 

For eksempel, hvis området er 1460 cm, vil din formel se sådan ud:


For eksempel, hvis basen er et rektangel med en længde på 8 cm og en bredde på 2 cm, skal du finde området som følger:



For eksempel, hvis arealet af basen er 16, vil din formel se sådan ud:



Husk, at de modsatte sider af et rektangel har samme længde. For eksempel, hvis basen er et rektangel med en længde på 8 cm og en bredde på 2 cm, skal du finde omkredsen som følger:



For eksempel, hvis omkredsen af basen er 20, vil din formel se sådan ud:


For eksempel i ligningen  træk først 32 fra hver side, og divider derefter hver side med 20. Dermed:
træk først 32 fra hver side, og divider derefter hver side med 20. Dermed:




Så højden på dit prisme er 71,4 cm. 

For eksempel, hvis området er 1460 cm, vil din formel se sådan ud:


Hvis du kender længden af alle tre sider af en trekant, kan du bestemme arealet ved hjælp af Herons formel.Læs Beregn arealet af en trekant for fuldstændige instruktioner. For eksempel, hvis trekantens basis er 8 cm, og trekantens højde er 4 cm, beregner du arealet som følger:




For eksempel, hvis arealet af basen er 16, vil din formel se sådan ud:



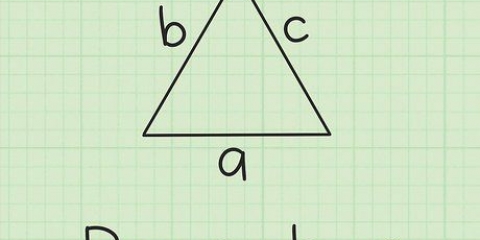
For eksempel, hvis basen er en trekant med længderne 8, 4 og 9 cm, beregner du omkredsen som følger:



Antag for eksempel, at omkredsen af basen er 21, vil din formel se sådan ud:


For eksempel i ligningen  , du skal først trække 32 fra hver side og derefter dividere hver side med 21. Dermed:
, du skal først trække 32 fra hver side og derefter dividere hver side med 21. Dermed:




Så højden af dit prisme er 68 cm.
Beregning af højden af et prisme
Indhold
- Trin
- Metode 1 af 4: Find højden af et rektangulært prisme med kendt volumen
- Metode 2 af 4: Bestemmelse af højden af et trekantet prisme med kendt volumen
- Metode 3 af 4: Find højden af et rektangulært prisme ved hjælp af dets areal
- Metode 4 af 4: Bestem højden af et trekantet prisme ved hjælp af dets areal
- Fornødenheder
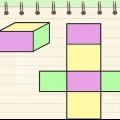
Et prisme er en tredimensionel figur med to parallelle baser, som er kongruente.Basens form afgør, hvilken type prisme det er, såsom et rektangulært eller trekantet prisme. Da det er en 3D-form, er det ikke ualmindeligt at ville beregne rumfanget af et prisme; dog skal du bruge prismets højde til det. Det er muligt at finde højden, når du har modtaget nok information: enten volumen, areal og omkreds af basen. Formlerne beskrevet i metoderne nedenfor er velegnede til prismer med baser af enhver form, forudsat at du kender formlen til at finde arealet af den form.
Trin
Metode 1 af 4: Find højden af et rektangulært prisme med kendt volumen

1. Brug formlen for rumfanget af et prisme. Rumfanget af et prisme kan findes ved hjælp af formlen  , hvorved
, hvorved  er lig med rumfanget af prismet,
er lig med rumfanget af prismet,  er lig med arealet af en base, og
er lig med arealet af en base, og  er lig med prismets højde.
er lig med prismets højde.
 , hvorved
, hvorved  er lig med rumfanget af prismet,
er lig med rumfanget af prismet,  er lig med arealet af en base, og
er lig med arealet af en base, og  er lig med prismets højde.
er lig med prismets højde. - Basen af et prisme er en af dets kongruente sider. Da alle modsatte sider af et rektangulært prisme er kongruente, kan enhver side bruges som jordplan, så længe du er i overensstemmelse med dine beregninger.

2. Påfør volumen på formlen. Hvis du ikke kender lydstyrken, kan du ikke bruge denne metode.
 ), vil din formel se sådan ud:
), vil din formel se sådan ud:

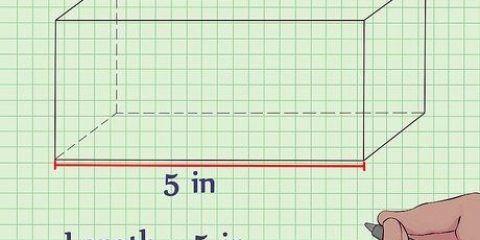
3. Find arealet af basen. For at finde arealet skal du kende længden og bredden af basen (eller af en side, hvis basen er en firkant). Brug formlen  at bestemme arealet af et rektangel.
at bestemme arealet af et rektangel.
 at bestemme arealet af et rektangel.
at bestemme arealet af et rektangel.


4. Erstat arealet af basen med volumenet af prismeformlen. Sørg for at erstatte variablen  .
.
 .
.

5. Løs ligningen for h  . Nu kender du højden af dit prisme.
. Nu kender du højden af dit prisme.
 . Nu kender du højden af dit prisme.
. Nu kender du højden af dit prisme. , du skal dividere hver side med 16 om
, du skal dividere hver side med 16 om  at beregne. Dermed:
at beregne. Dermed:

Så højden af det rektangulære prisme er 4 meter.
Metode 2 af 4: Bestemmelse af højden af et trekantet prisme med kendt volumen

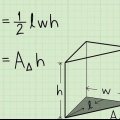
1. Skriv formlen for rumfanget af et prisme ned. Rumfanget af ethvert prisme kan findes ved hjælp af formlen  ,hvorved
,hvorved  er lig med rumfanget af prismet,
er lig med rumfanget af prismet,  er lig med arealet af en base, og
er lig med arealet af en base, og  er lig med prismets højde.
er lig med prismets højde.
 ,hvorved
,hvorved  er lig med rumfanget af prismet,
er lig med rumfanget af prismet,  er lig med arealet af en base, og
er lig med arealet af en base, og  er lig med prismets højde.
er lig med prismets højde. - Basen af et prisme er en af dets kongruente sider. Basen af et trekantet prisme er en trekant. Siderne er rektangler.

2. Påfør volumen på formlen. Hvis du ikke kender lydstyrken, kan du ikke bruge denne metode.
 ), vil din formel se sådan ud:
), vil din formel se sådan ud:

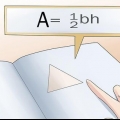
3. Find arealet af basen. For at finde arealet skal du kende længden af trekantens base og højden af trekanten. Brug formlen  til at bestemme arealet af en trekant.
til at bestemme arealet af en trekant.
 til at bestemme arealet af en trekant.
til at bestemme arealet af en trekant.



4. Erstat arealet af basen med volumenet af prismeformlen. Sørg for at erstatte variablen  .
.
 .
.

5. Løs ligningen for h  . Nu kender du højden af dit prisme.
. Nu kender du højden af dit prisme.
 . Nu kender du højden af dit prisme.
. Nu kender du højden af dit prisme. , du skal dividere hver side med 42 for at bestemme
, du skal dividere hver side med 42 for at bestemme  . Dermed:
. Dermed:

Metode 3 af 4: Find højden af et rektangulært prisme ved hjælp af dets areal

1. Skriv formlen for arealet af et prisme. Formlen for arealet af et prisme er  , hvorved
, hvorved  er lig med overfladen,
er lig med overfladen,  er lig med arealet af basen,
er lig med arealet af basen,  er lig med omkredsen af basen, og
er lig med omkredsen af basen, og  er lig med prismets højde.
er lig med prismets højde.
 , hvorved
, hvorved  er lig med overfladen,
er lig med overfladen,  er lig med arealet af basen,
er lig med arealet af basen,  er lig med omkredsen af basen, og
er lig med omkredsen af basen, og  er lig med prismets højde.
er lig med prismets højde. - For at denne metode skal fungere, skal du kende området af prismet samt længden og bredden af basen.

2. Erstat arealet af prismet i formlen. Hvis overfladen er ukendt, vil denne metode ikke fungere.


3. Find arealet af basen. For at finde området skal du kende længden og bredden af basen (eller den ene side, hvis basen er en firkant). Brug formlen  at bestemme arealet af et rektangel.
at bestemme arealet af et rektangel.
 at bestemme arealet af et rektangel.
at bestemme arealet af et rektangel.


4. Erstat arealet af basen i formlen for arealet af et prisme, og forenkle. Sørg for at udfylde brevet  .
.
 .
.


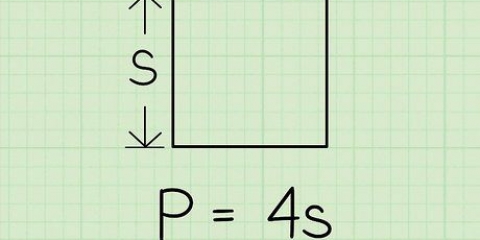
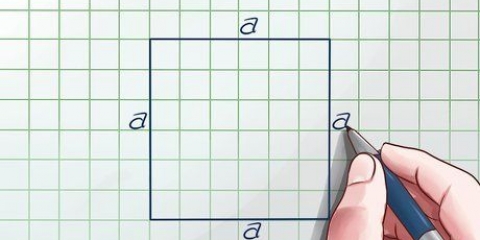
5. Bestem omkredsen af basen. For at finde omkredsen af et rektangel skal du lægge længderne af alle fire sider sammen eller gange længden af en side med 4, hvis det er en firkant.



6. Erstat omkredsen af basen i formlen for arealet af et prisme. Sørg for at erstatte bogstavet  .
.
 .
.

7. Løs ligningen for h  . Nu kender du højden af dit prisme.
. Nu kender du højden af dit prisme.
 . Nu kender du højden af dit prisme.
. Nu kender du højden af dit prisme. træk først 32 fra hver side, og divider derefter hver side med 20. Dermed:
træk først 32 fra hver side, og divider derefter hver side med 20. Dermed:



Metode 4 af 4: Bestem højden af et trekantet prisme ved hjælp af dets areal

1. Skriv formlen for arealet af et prisme. Formlen for arealet af et prisme er  , hvorved
, hvorved  er lig med overfladen,
er lig med overfladen,  er lig med arealet af basen,
er lig med arealet af basen,  er lig med omkredsen af basen, og
er lig med omkredsen af basen, og  er lig med prismets højde.
er lig med prismets højde.
 , hvorved
, hvorved  er lig med overfladen,
er lig med overfladen,  er lig med arealet af basen,
er lig med arealet af basen,  er lig med omkredsen af basen, og
er lig med omkredsen af basen, og  er lig med prismets højde.
er lig med prismets højde. - For at denne metode skal fungere, skal arealet af prismet være kendt, såvel som arealet af den trekantede base og længden af alle tre sider af basen.

2. Erstat arealet af prismet i formlen. Hvis overfladen ikke er kendt, vil denne metode ikke fungere.


3. Find arealet af basen. For at finde arealet skal du kende længden af trekantens base og højden af trekanten. Brug formlen  til at bestemme arealet af en trekant.
til at bestemme arealet af en trekant.
 til at bestemme arealet af en trekant.
til at bestemme arealet af en trekant.



4. Erstat arealet af basen i formlen for arealet af et prisme og forenkle. Stedfortræder for  .
.
 .
.


5. Bestem omkredsen af basen. For at finde omkredsen af en trekant skal du lægge længderne af alle tre sider sammen.



6. Erstat omkredsen af basen i formlen for arealet af et prisme. Sørg for at erstatte  .
.
 .
.

7. Løs ligningen for h  . Nu kender du højden af dit prisme.
. Nu kender du højden af dit prisme.
 . Nu kender du højden af dit prisme.
. Nu kender du højden af dit prisme. , du skal først trække 32 fra hver side og derefter dividere hver side med 21. Dermed:
, du skal først trække 32 fra hver side og derefter dividere hver side med 21. Dermed:



Fornødenheder
- Pen/blyant og papir eller lommeregner (valgfrit)
Artikler om emnet "Beregning af højden af et prisme"
Оцените, пожалуйста статью
Lignende
Populær