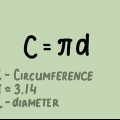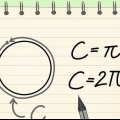Sådan beregnes radius af en cirkel

Indhold

Trin

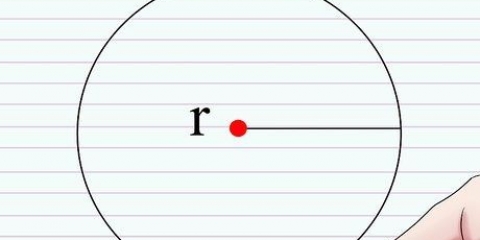
Radius af en cirkel er afstanden fra centrum af cirklen til kanten. Diameteren af en cirkel er længden af den lige linje, der kan trækkes mellem to punkter på kuglen eller cirklen og gennem dens centrum.Du bliver ofte bedt om at beregne radius af en cirkel baseret på andre data. I denne artikel lærer du, hvordan du beregner radius af en cirkel baseret på en given diameter, omkreds og areal. Den fjerde metode er en mere avanceret metode til at bestemme centrum og radius af en cirkel baseret på koordinaterne for tre punkter på cirklen.

Trin

Metode 1 af 3: Beregn radius, hvis du kender diameteren

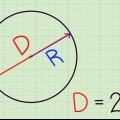
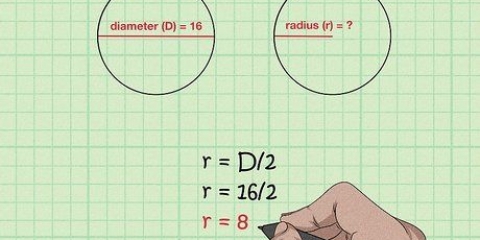
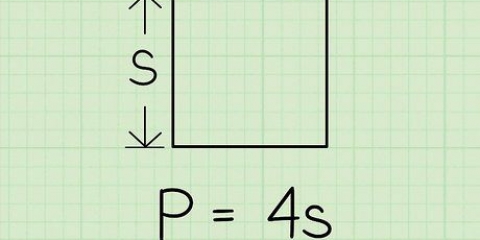
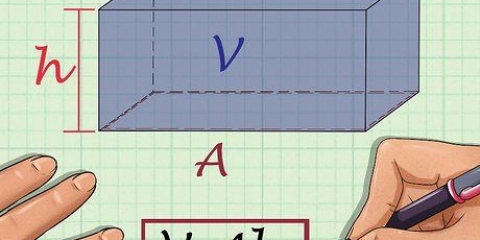
1. Husk hvad diameteren er. Diameteren af en cirkel er længden af den lige linje, der kan trækkes mellem to punkter på kuglen eller cirklen og gennem dens centrum. Diameteren er den længste linje, der kan trækkes gennem en cirkel og deler cirklen i to halvdele. Længden af diameteren er også lig med længden af to gange radius. Formlen for diameteren er som følger: D= 2r, hvor "d" står for diameter og "r" til bjælke. Formlen for radius kan udledes af den foregående formel og er derfor: r = D/2.

Billede med titlen Beregn radius af en cirkel Trin 2

2. Divider diameteren med 2 for at finde radius. Hvis du kender diameteren af en cirkel, skal du bare dividere den med 2 for at finde radius.

For eksempel, hvis diameteren af en cirkel er 4, så er den lige 4/2 eller 2.

Metode 2 af 3: Beregn radius, hvis du kender omkredsen

Billede med titlen Beregn radius af en cirkel Trin 3

1. Kan du huske formlen for en cirkels omkreds?. Omkredsen af en cirkel er afstanden omkring cirklen. En anden måde at se det på er denne: omkredsen er længden af den linje, du får, hvis du skærer cirklen op i et punkt og lægger linjen lige. Formlen for en cirkels omkreds er O = 2πr, hvor "r" er radius og π er konstanten pi eller 3,14159... Formlen for radius er da r = O/2π.

Normalt kan du afrunde pi til to cifre efter decimaltegnet (3,14), men tjek først med din lærer.

Billede med titlen Beregn radius af en cirkel Trin 4

2. Beregn radius med den angivne omkreds. For at beregne radius baseret på omkredsen skal du dividere omkredsen med 2π eller 6,28

For eksempel, hvis omkredsen er 15, så er radius r = 15/2π eller 2,39.

Metode 3 af 3: Beregn radius, hvis du kender koordinaterne til tre punkter på cirklen

Billede med titlen Beregn radius af en cirkel Trin 9

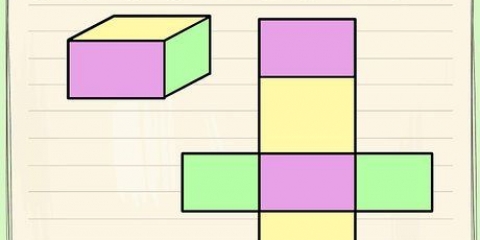
1. Forstå, at tre punkter kan definere en cirkel. Alle tre punkter på et gitter definerer en cirkel, der tangerer de tre punkter. Det er den omskrevne cirkel i trekanten, der danner punkterne. Cirklens centrum kan falde inden for eller uden for trekanten, afhængigt af placeringen af de tre punkter, og det er samtidig "vejkryds" af trekanten.Det er muligt at beregne radius af cirklen, hvis du kender xy-koordinaterne for de tre pågældende punkter.

Lad os som et eksempel tage tre punkter defineret som følger: P1 = (3,4), P2 = (6, 8) og P3 = (-1, 2).

Billede med titlen Beregn radius af en cirkel Trin 10

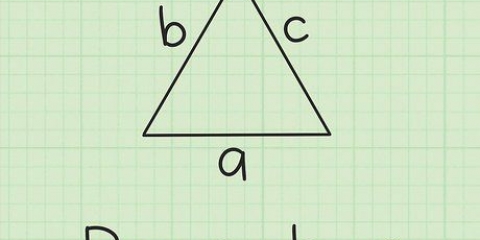
2. Brug afstandsformlen til at beregne længderne af trekantens tre sider, som vi kalder a, b og c. Formlen for afstanden mellem to koordinater (x₁, y₁) og (x₂, y₂) er som følger: afstand = √(( x₂ - x₁) + (y₂ - y₁)). Bearbejd nu koordinaterne for de tre punkter i denne formel for at finde længderne af trekantens tre sider.

Billede med titlen Beregn radius af en cirkel Trin 11

3. Beregn længden af den første side a, som løber fra punkt P1 til P2. I vores eksempel er koordinaterne for P1 (3.4) og P2 (6.8), så længden af siden a = √((6 - 3) + (8 - 4)).

a = √(3 + 4)

a = √(9 + 16)

a = √25

a = 5

Billede med titlen Beregn radius af en cirkel Trin 12

4. Gentag processen for at finde længden af den anden side b, som går fra P2 til P3. I vores eksempel er koordinaterne for P2 (6.8) og P3 (-1.2), så længden af siden b = √((-1 - 6) + (2 - 8)).

b= √(-7 + -6)

b = √(49 + 36)

b = √85

b = 9.23

Billede med titlen Beregn radius af en cirkel Trin 13

5. Gentag processen for at finde længden af den tredje side c, som går fra P3 til P1. I vores eksempel er koordinaterne for P3 (-1,2) og P1 (3,4), så længden af siden c =√((3 - -1) + (4 - 2)).

c= √(4 + 2)

c = √(16 + 4)

c = √20

c = 4.47

Billede med titlen Beregn radius af en cirkel Trin 14

6. Brug disse længder i radiusfindingsformlen: (abc)/(√(a + b + c)(b + c - a)(c + a - b)(a + b - c)).. Resultatet er radius af vores cirkel!

Længderne af trekanten er som følger: a = 5, b = 9.23 og c = 4.47. Så formlen for radius ser således ud: r = (5 * 9.23*4.47)/(√(5 + 4.47 + 9.23)(4.47 + 9.23 - 5)(9.23 + 5 - 4.47)(5 + 4.47 – 9.23)).