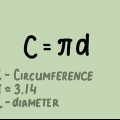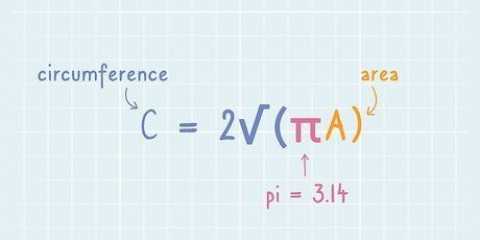Radius (r) af en cirkel er afstanden fra et punkt på cirklen til midten af cirklen. Diameteren (d) af en cirkel er afstanden fra et punkt på cirklen til et andet punkt lige over for cirklen, der går gennem cirklens centrum. Det græske bogstav pi (π) står for forholdet mellem omkredsen divideret med diameteren og er repræsenteret ved tallet 3,14159265..., et irrationelt tal, der hverken har et sidste ciffer eller et genkendeligt mønster af gentagne cifre. Dette tal afrundes ofte til 3,14 for standardberegninger. 
I de fleste matematikopgaver er radius eller diameter givet. 
For eksempel: Hvad er omkredsen af en cirkel med en radius på 3 cm? Skriv formlen: C = 2πr Udfyld variablerne: C = 2π3 Multiplicer: C = (2*3*π) = 6π = 18,84 cm For eksempel: Hvad er omkredsen af en cirkel med en diameter på 9 m? Skriv formlen ned: C = πd Udfyld variablerne: C = 9π Multiplicer: C = (9*π) = 28,26 m 
Bestem omkredsen af en cirkel med en diameter på 5 m. C = πd = 5π = 15,7 m Bestem omkredsen af en cirkel med en radius på 10 m. C = 2πr = C = 2π10 = 2 *10 *π = 62,8 m. 

Radius (r) af en cirkel er afstanden fra et punkt på cirklen til midten af cirklen. Diameteren (d) af en cirkel er afstanden fra et punkt på cirklen til et andet punkt lige over for cirklen, der går gennem cirklens centrum. Det græske bogstav pi (π) står for forholdet mellem omkredsen divideret med diameteren og er repræsenteret ved tallet 3,14159265..., et irrationelt tal, der hverken har et sidste ciffer eller et genkendeligt mønster af gentagne cifre. Dette tal afrundes normalt til 3,14 for grundlæggende beregninger. 
I de fleste matematikopgaver er radius eller diameter givet. 
For eksempel: hvad er arealet af en cirkel med en radius på 3 m? Skriv formlen: A = r. Udfyld variablerne: A = π3. Kvadret radius: r = 3 = 9 Multiplicer med pi: -en = 9π = 28,26 m For eksempel: hvad er arealet af en cirkel med en diameter på 4 m? Skriv formlen: A = π(d/2). Udfyld variablerne: A = π(4/2). Divider diameteren med 2: d/2 = 4/2 = 2 Kvadret resultatet: 2 = 4 Multiplicer med pi: -en = 4π = 12,56 m 
Find arealet af en cirkel med en diameter på 7 m. A = π(d/2) = π(7/2) = π(3,5) = 12,25 * π= 38,47 m. Find arealet af en cirkel med en radius på 3 m. A = πr = π * 3 = 9 * π = 28,26 m 

For eksempel: Beregn omkredsen af en cirkel med en radius på (x + 1). Skriv formlen: C = 2πr Udfyld de givne oplysninger: C = 2π(x+1) 
For eksempel: Beregn omkredsen af en cirkel med en radius på (x = 1). C = 2πr = 2π(x+1) = 2πx + 2π1 = 2πx +2π = 6,28x + 6,28 Hvis værdien af `x` er angivet senere i opgaven, kan du tilslutte den og få et helt tal. 
Find arealet af en cirkel med en radius på 2x. A = πr = π(2x) = π4x = 12,56x Find arealet af en cirkel med en diameter på (x + 2). A = π(d/2) = π((x +2)/2) = ((x +2)/4)π
Beregning af omkreds og areal af en cirkel
Indhold
Omkredsen (C) af en cirkel er dens omkreds eller afstanden omkring den. Arealet (A) af en cirkel er, hvor meget plads cirklen optager eller arealet omgivet af cirklen. Både areal og omkreds kan beregnes med simple formler ud fra radius eller diameter af cirklen og værdien af pi.
Trin
Del 1 af 3: Beregning af omkredsen

1. Lær formlen for omkredsen af en cirkel. Der er to formler, der kan bruges til at beregne omkredsen af en cirkel: C = 2πr eller C = d, hvor π er den matematiske konstant og omtrent lig med 3,14,r er lig med radius og d lig med diameteren.
- Da radius af en cirkel er lig med to gange dens diameter, er disse ligninger i det væsentlige de samme.
- Enhederne for omkredsen kan være enhver enhed for længdemålet: kilometer, meter, centimeter osv.

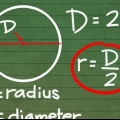
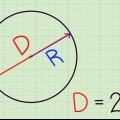
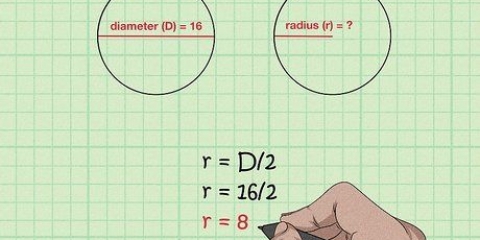
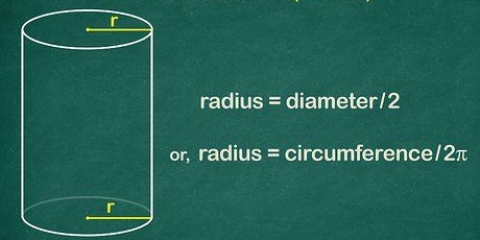
2. Forstå de forskellige dele af formlen. Der er tre komponenter til at finde omkredsen af en cirkel: radius, diameter og π. Radius og diameter hænger sammen: radius er lig med halvdelen af diameteren, mens diameteren er lig med to gange radius.

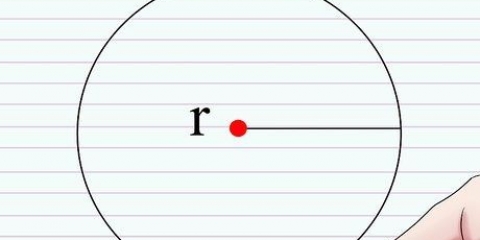
3. Mål radius eller diameter af cirklen. Placer en lineal på den ene kant af cirklen, gennem midten og til den anden side af cirklen. Afstanden fra centrum af cirklen er radius, mens afstanden fra den anden ende af cirklen er diameteren.

4. Bearbejde og løse variablerne. Når du har bestemt radius og/eller diameter af cirklen, kan du sætte disse variable ind i den passende ligning. Hvis du har bjælken, brug C = 2πr, men hvis du kender diameteren så brug C = d.

5. Øv dig med et par eksempler. Nu hvor du har lært formlen, er det tid til at øve dig med nogle eksempler. Jo flere problemer du løser, jo lettere bliver det at løse dem i fremtiden.
Del 2 af 3: Beregning af areal

1. Lær formlen for arealet af en cirkel. Arealet af en cirkel kan beregnes ved hjælp af enten dens diameter eller dens radius med to forskellige formler: A = r eller A = π(d/2), hvor π er den matematiske konstant omtrent lig med 3,14,r radius og d diameteren.
- Da radius af en cirkel er lig med halvdelen af dens diameter, er disse ligninger i det væsentlige de samme.
- Enhederne for areal kan være en hvilken som helst enhed for længde i anden kvadrat: km i kvadrat (km), kvadratmetre (m), kvadratcentimeter (cm) osv.

2. Forstå de forskellige dele af formlen. Der er tre komponenter til at finde omkredsen af en cirkel: radius, diameter og π. Radius og diameter er relateret til hinanden: radius er lig med halvdelen af diameteren, mens diameteren er lig med dobbelt radius.

3. Mål radius eller diameter af cirklen. Placer den ene ende af en lineal i et punkt på cirklen, gennem midten og til den anden side af cirklen. Afstanden fra centrum af cirklen er radius, mens afstanden fra det andet punkt på cirklen er diameteren.

4. Udfyld variablerne og løs dem. Når du har bestemt radius og/eller diameter af cirklen, kan du sætte disse variable ind i den passende ligning. Hvis du kender radius, så brug A = r, men hvis du kender diameteren så brug A = π(d/2).

5. Øv dig med et par eksempler. Nu hvor du har lært formlen, er det tid til at øve dig med nogle eksempler. Jo flere problemer du løser, jo lettere bliver det at løse andre problemer.
Del 3 af 3: Beregning af arealet og omkredsen med variable

1. Bestem radius eller diameter af cirklen. Nogle problemer giver en radius eller diameter med en variabel, såsom r = (x + 7) eller d = (x + 3). I dette tilfælde kan du stadig bestemme arealet eller omkredsen, men dit endelige svar vil også indeholde denne variabel. Skriv radius eller diameter ned som angivet i erklæringen.
- For eksempel: Beregn omkredsen af en cirkel med en radius på (x = 1).

2. Skriv formlen med de givne oplysninger. Uanset om du vil beregne areal eller omkreds, følger du stadig de grundlæggende trin for at udfylde, hvad du ved. Skriv formlen for areal eller omkreds og udfyld derefter de givne variable.

3. Løs problemet, som om variablen var et tal. På dette tidspunkt kan du bare løse problemet, som du plejer, og behandle variablen, som om den blot var et andet tal. Du har muligvis brug for ved at bruge fordelingsejendomme for at forenkle det endelige svar.

4. Øv dig med nogle eksempler. Nu hvor du har lært formlen, er det tid til at øve dig med nogle eksempler. Jo flere problemer du løser, jo lettere bliver det at løse nye.
Artikler om emnet "Beregning af omkreds og areal af en cirkel"
Оцените, пожалуйста статью
Populær