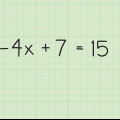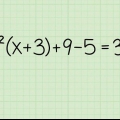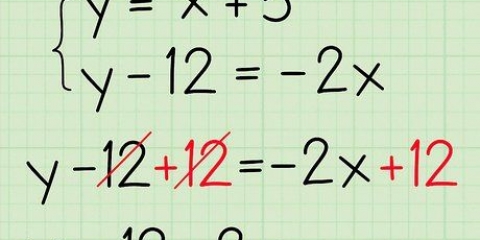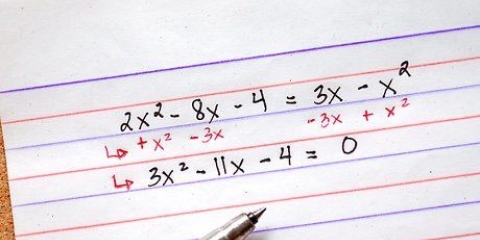Brug af fordelingsegenskaben til at løse en ligning

Indhold

Trin
Tips

Den distributive egenskab er en regel i matematik for at forenkle en ligning med parenteser. Du lærte sikkert tidligt, at du først skal udføre operationerne i parentes, men med algebraiske udtryk er det ikke altid muligt. Den fordelende egenskab giver dig mulighed for at gange udtrykket uden for parentes med termerne inde i det. Du skal passe på, at du gør det på den rigtige måde, ellers kan du miste information, og sammenligningen er ikke længere korrekt. Du kan også bruge den fordelende egenskab til at forenkle ligninger med brøker.

Trin

Metode 1 af 4: Brug af Fundamental Distributive Property

1. Multiplicer udtrykket uden for parentes med et hvilket som helst led inden for parentes. For at gøre dette opdeler du i det væsentlige det ydre led mellem de indre udtryk. Gang udtrykket uden for parentes med det første led inden for parentes. Så gange du det med det andet led. Hvis der er mere end to led, skal du fortsætte med at fordele udtrykket uden for parentes på tværs af alle led inden for parentesen. Lad blot operatorerne (plus eller minus) være inden for parentesen.

$2 (x - 3) = 10$ $2(x-3)=10$
$2 (x) - (2) (3) = 10$ $2(x)-(2)(3)=10$
$2 x - 6 = 10$ $2x-6=10$

Billede med titlen Brug fordelingsegenskab til at løse en ligning Trin 2

2. Kombiner lignende udtryk. Før du kan løse ligningen, skal du kombinere ens udtryk. Kombiner alle numeriske udtryk med hinanden. Derudover kombinerer du alle variable termer separat. For at forenkle ligningen skal du bestille vilkårene, så variablerne er på den ene side af lighedstegnet og konstanterne (kun tallene) er på den anden side.

2 x - 6 = 10

$2x-6=10$ ....(oprindeligt problem)

2 x - 6 (+ 6) = 10 (+ 6)

$2x-6(+6)=10(+6)$ .... (tilføj 6 på begge sider)

2 x = 16

$2x=16$ .... (Variabel venstre; konstant højre)

Billede med titlen Brug fordelingsegenskab til at løse en ligning Trin 3

3. Løs ligningen. løs

x

$x$ ved at dividere begge sider af ligningen med koefficienten for variablen.

2 x = 16

$2x=16$ ....(oprindeligt problem)

2 x / 2 = 16 / 2

$2x/2=16/2$ ....(divider begge sider med 2)

x = 8

$x=8$ ....(opløsning)

Metode 2 af 4: Fordel negative koefficienter

Billede med titlen Brug fordelingsegenskab til at løse en ligning Trin 4

1. Fordel et negativt tal sammen med minustegnet. Hvis du skal gange et led eller udtryk i parentes med et negativt tal, skal du sørge for at anvende minustegnet på hvert led inden for parentesen.

Husk de grundlæggende regler for at gange med negative tal:

Minus x Minus = Plus.
Minus x Plus = Minus.

Se på følgende eksempel:

- 4 (9 - 3 x) = 48

$-4(9-3x)=48$ .... (oprindeligt problem)

- 4 (9) - (- 4) (3 x) = 48

$-4(9)-(-4)(3x)=48$ ....(gang -4 med hvert led)

- 36 - (- 12 x) = 48

$-36-(-12x)=48$ ....(forenkle multiplikationen)

- 36 + 12 x = 48

$-36+12x=48$ ....(bemærk at `minus -12` er det samme som +12)

Billede med titlen Brug fordelingsegenskab til at løse en ligning Trin 5

2. Kombiner lignende udtryk. Når du har gennemført fordelingen, skal du forenkle ligningen ved at flytte alle variabelled til den ene side af lighedstegnet og alle tal uden variable til den anden side. Det gør du ved hjælp af en kombination af addition eller subtraktion.

- 36 + 12 x = 48

$-36+12x=48$ ....(oprindeligt problem)

- 36 (+ 36) + 12 x = 48 + 36

$-36(+36)+12x=48+36$ ....(tilføj 36 til hver side)

12 x = 84

$12x=84$ ....(forenkle tilføjelsen for at isolere variablen)

Billede med titlen Brug fordelingsegenskab til at løse en ligning Trin 6

3. Del for at få den endelige løsning. Løs ligningen ved at dividere begge sider af ligningen med koefficienten for variablen. Dette skulle resultere i en enkelt variabel på den ene side af ligningen, med resultatet på den anden side.

12 x = 84

$12x=84$ ....(oprindeligt problem)

12 x / 12 = 84 / 12

$12x/12=84/12$ ....(divider begge sider med 12)

x = 7

$x=7$ ....(opløsning)

Billede med titlen Brug fordelingsegenskab til at løse en ligning Trin 7

4. Behandl subtraktion som addition (fra -1). Når du ser et minustegn i et algebraproblem, især hvis det er før en parentes, står der i det væsentlige + (-1). Dette hjælper med at fordele minustegnet korrekt på tværs af alle led i parentes. Løs derefter problemet som før.

Overvej for eksempel problemet,

4 x - (x + 2) = 4

$4x-(x+2)=4$ . For at sikre, at du har fordelt minustegnet korrekt, skal du omskrive problemet sådan her:

4 x + (- 1) (x + 2) = 4

$4x+(-1)(x+2)=4$

Så fordeler du -1 over vilkårene i parentes, som følger:

4 x + (- 1) (x + 2) = 4

$4x+(-1)(x+2)=4$ ....(ændret problem)

4 x - x - 2 = 4

$4x-x-2=4$ ....(gang -1 med x og med 2)

3 x - 2 = 4

$3x-2=4$ ....(kombiner udtryk)

3 x - 2 + 2 = 4 + 2

$3x-2+2=4+2$ ....(tilføj 2 på begge sider)

3 x = 6

$3x=6$ ....(forenkle vilkår)

3 x / 3 = 6 / 3

$3x/3=6/3$ ....(divider begge sider med 3)

x = 2

$x=2$ ....(opløsning)

Metode 3 af 4: Brug den fordelende egenskab til at simplificere brøker

Billede med titlen Brug fordelingsegenskab til at løse en ligning Trin 8

1. Find ud af, om der er brøkkoefficienter eller konstanter. Nogle gange skal du måske løse et problem med brøker som koefficienter eller konstanter. Du kan lade dem være som de er og anvende algebraens grundlæggende regler på dem for at løse problemet. Ved at bruge den fordelende egenskab kan man dog ofte forenkle løsningen ved at konvertere brøkerne til heltal.

Tjek følgende eksempel $x - 3 = \frac{x}{3} + \frac{1}{6}$ $x-3={frac{x}{3}}+{frac{1}{6}}$ . Brøkerne i dette eksempel er $\frac{x}{3}$ ${frac{x}{3}}$ og $\frac{1}{6}$ ${frac{1}{6}}$ .

Billede med titlen Brug fordelingsegenskab til at løse en ligning Trin 9

2. Find det mindste fælles multiplum (LCM) for alle nævnere. På dette trin kan du ignorere alle heltal. Bare se på brøkerne og bestem LCF for alle nævnere. Bestem kgf ved at lede efter det mindste tal, der er et multiplum af nævnerne af begge brøker i ligningen. I dette eksempel er nævnerne 3 og 6, så 6 er kgf.

Billede med titlen Brug fordelingsegenskab til at løse en ligning Trin 10

3. Gang alle led i ligningen med kgf. Husk, du kan anvende enhver operation på en matematisk ligning, så længe du gør det på begge sider. Ved at gange hvert led i ligningen med lcg ophæver vilkårene hinanden og `bliver` til heltal. Placer dine parenteser rundt om hele venstre og højre side af ligningen, og lav derefter fordelingen:

x - 3 = \frac{x}{3} + \frac{1}{6}

$x-3={frac{x}{3}}+{frac{1}{6}}$ ....(oprindelig ligning)

(x - 3) = (\frac{x}{3} + \frac{1}{6})

$(x-3)=({frac{x}{3}}+{frac{1}{6}})$ ....(anvend parentes)

6 (x - 3) = 6 (\frac{x}{3} + \frac{1}{6})

$6(x-3)=6({frac{x}{3}}+{frac{1}{6}})$ ....(multiplicer begge sider med kgf)

6 x - 6 (3) = 6 (\frac{x}{3}) + 6 (\frac{1}{6})

$6x-6(3)=6({frac{x}{3}})+6({frac{1}{6}})$ ....(fordel multiplikation)

6 x - 18 = 2 x + 1

$6x-18=2x+1$ ....(forenkle multiplikation)

Billede med titlen Brug fordelingsegenskab til at løse en ligning Trin 11

4. Kombiner lignende udtryk. Kombiner alle led, så alle variable er på den ene side af ligningen, og alle konstanter er på den anden side. Brug de grundlæggende additions- og subtraktionsoperationer til at flytte led fra den ene side af ligningen til den anden.

6 x - 18 = 2 x + 1

$6x-18=2x+1$ ....(forenklet problem)

6 x - 2 x - 18 = 2 x - 2 x + 1

$6x-2x-18=2x-2x+1$ ....(træk 2x fra begge sider)

4 x - 18 = 1

$4x-18=1$ ....(forenkle minus sum)

4 x - 18 + 18 = 1 + 18

$4x-18+18=1+18$ ....(tilføj 18 på begge sider)

4 x = 19

$4x=19$ ....(forenkle tilføjelse)

Billede med titlen Brug fordelingsegenskab til at løse en ligning Trin 12

5. Løs ligningen. Find den endelige løsning ved at dividere begge sider af ligningen med variablens koefficient. Dette efterlader dig med x på den ene side af ligningen og den numeriske løsning på den anden.

4 x = 19

$4x=19$ ....(tilpasset problem)

4 x / 4 = 19 / 4

$4x/4=19/4$ ....(divider begge sider med 4)

x = \frac{19}{4} eller 4 \frac{3}{4}

$x={frac{19}{4}}{text{ eller }}4{frac{3}{4}}$ ....(endelig løsning)

Metode 4 af 4: Fordel en brøk med en ligning

Billede med titlen Brug fordelingsegenskab til at løse en ligning Trin 13

1. Fortolk en brøk med en ligning som en fordelt division. Nogle gange ser du et problem med flere led i tælleren af en brøk over en fællesnævner. Du skal behandle dette som et fordelingsproblem og anvende nævneren på hvert led i tælleren. Du kan omskrive brøken for at vise fordelingen. Som følger:

$4 x + 8 2 = 4$ ${frac{4x+8}{2}}=4$ .....(oprindeligt problem)
$4 x 2 + \frac{8}{2} = 4$ ${frac{4x}{2}}+{frac{8}{2}}=4$ .....(multiplicer nævneren med hvert led i tælleren)

Billede med titlen Brug fordelingsegenskab til at løse en ligning Trin 14

2. Forenkle hver tæller som separat brøk. Efter at have fordelt divisoren over hvert led, kan du derefter forenkle hvert led individuelt.

4 x 2 + \frac{8}{2} = 4

${frac{4x}{2}}+{frac{8}{2}}=4$ .....(tilpasset problem)

2 x + 4 = 4

$2x+4=4$ .....(forenkle brøkerne)

Billede med titlen Brug fordelingsegenskab til at løse en ligning Trin 15

3. Isoler variablen. Fortsæt med at løse problemet ved at isolere variablen på den ene side af ligningen og flytte de konstante led til den anden side. Gør dette gennem en kombination af addition og subtraktion, hvor det er nødvendigt.

2 x + 4 = 4

$2x+4=4$ .....(tilpasset problem)

2 x + 4 - 4 = 4 - 4

$2x+4-4=4-4$ .....(træk 4 fra fra begge sider)

2 x = 0

$2x=0$ .....(isoler x på den ene side)

Billede med titlen Brug fordelingsegenskab til at løse en ligning Trin 16

4. Divider med koefficienten for at løse problemet. I det sidste trin dividerer du med variablens koefficient. Dette giver den endelige løsning, med den enkelte variabel på den ene side af ligningen og den numeriske løsning på den anden side.

2 x = 0

$2x=0$ .....(tilpasset problem)

2 x / 2 = 0 / 2

$2x/2=0/2$ .....(divider begge sider med 2)

x = 0

$x=0$ .....(opløsning)

Billede med titlen Brug fordelingsegenskab til at løse en ligning Trin 17

5. Undgå den almindelige fejl at dele kun ét udtryk. Det er fristende (men forkert) at dividere det første led i tælleren med nævneren og eliminere brøken. En fejl som denne ville se sådan ud for ovenstående problem:

4 x + 8 2 = 4

${frac{4x+8}{2}}=4$ .....(oprindeligt problem)

2 x + 8 = 4

$2x+8=4$ .....(kun 4x divideres med 2 i stedet for hele tælleren)

2 x + 8 - 8 = 4 - 8

$2x+8-8=4-8$

2 x = - 4

$2x=-4$

x = - 2

$x=-2$ ..... (forkert løsning)

Billede med titlen Brug fordelingsegenskab til at løse en ligning Trin 18

6. Tjek rigtigheden af din løsning. Du kan altid tjekke dit arbejde ved at indsætte din løsning i det oprindelige problem. Når du vil forenkle, skal du nå frem til et sandt udsagn. Hvis du forenkler og får et forkert udsagn som svar, så er din løsning forkert. I dette eksempel tester du de to løsninger for x = 0 og x =-2 for at se, hvilken der er korrekt.

Start med løsning x=0:

4 x + 8 2 = 4

${frac{4x+8}{2}}=4$ .....(oprindeligt problem)

4 (0) + 8 2 = 4

${frac{4(0)+8}{2}}=4$ .....(erstat x med 0)

0 + 8 2 = 4

${frac{0+8}{2}}=4$

\frac{8}{2} = 4

${frac{8}{2}}=4$

4 = 4

$4=4$ .....(Rigtigt. Dette er den rigtige løsning.)

Prøv den `forkerte løsning for x=-2:

4 x + 8 2 = 4

${frac{4x+8}{2}}=4$ .....(oprindeligt problem)

4 (- 2) + 8 2 = 4

${frac{4(-2)+8}{2}}=4$ .....(indtast -2 for x)

- 8 + 8 2 = 4

${frac{-8+8}{2}}=4$

\frac{0}{2} = 4

${frac{0}{2}}=4$

0 = 4

$0=4$ .....(Forkert udsagn. Derfor er x=-2 falsk.)

Tips

Du kan også bruge den distributive egenskab til at forenkle nogle multiplikationer. Du kan opdele tal i tiere med en rest for at gøre hovedregning lettere. For eksempel kan du omskrive 8 x 16 som 8(10+6). Dette er så simpelthen 80 + 48 = 128. Et andet eksempel, 7 x 24 = 7(20 + 4) = 7(20) + 7(4) = 140 + 28 = 168. Øv disse udenad, og hovedregning bliver meget nemmere.