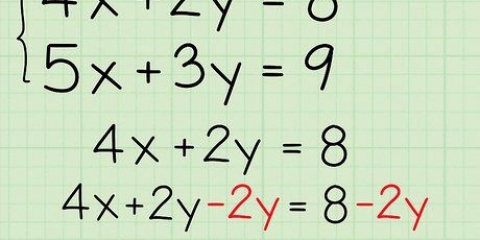Løs en ligning i to trin

Indhold

Trin
Tips

Ligninger, som du kan løse i to trin, er relativt nemme – det tager trods alt kun to trin. For at løse en sådan ligning skal du bare isolere variablen ved at addere, subtrahere, gange eller dividere. Hvis du vil vide, hvordan og på hvilken måde du løser ligninger i to trin, skal du følge instruktionerne nedenfor.

Trin

Metode 1 af 3: Løsning af ligninger med én variabel

1. Skriv problemet ned. Det første skridt til at løse sådan en ligning er at skrive den ned, så du kan få et bedre overblik over problemet. Antag, at vi har følgende problem: -4x + 7 = 15.

Billede med titlen Solve Two Step Algebraic Equations Trin 2

2. Beslut om du vil bruge addition eller subtraktion for at isolere det ønskede udtryk. Det næste trin er at finde en måde at efterlade -4x på den ene side og konstanterne (heltallene) på den anden side. For at gøre dette skal du finde det modsatte af +7, hvilket er -7. Træk 7 fra begge sider af ligningen for at eliminere +7, der er på samme side som variablen. Bare skriv -7 under 7 på den ene side og under 15 på den anden side, så ligningen er rigtig på begge sider.

Husk algebraens gyldne regel. Hvad du gør på den ene side af ligningen, skal du gøre på den anden side for at gøre det rigtigt. Derfor blev 7 også trukket fra 15. De 7 skal kun trækkes fra én gang pr. Derfor trækkes det ikke fra -4x.

Billede med titlen Solve Two Step Algebraic Equations Trin 3

3. Forøg eller formindsk ligningen på begge sider. Herefter isoleres variablen. Hvis du trækker 7 fra venstre side af ligningen, bliver denne side 0, mens 8 efterlades på højre side af ligningen. Så den nye ligning bliver -4x = 8.

-4x + 7 = 15 =

-4x = 8

Billede med titlen Solve Two Step Algebraic Equations Trin 4

4. Fjern variablens koefficient ved at gange eller dividere. Koefficienten er det tal, der er knyttet til variablen. I dette eksempel er koefficienten -4. For at fjerne -4 fra -4x skal du dividere begge sider af ligningen med -4.

Igen, hvad du gør på den ene side af ligningen, skal du gøre på den anden side.Det er derfor, der står to gange ÷ -4.

Billede med titlen Solve Two Step Algebraic Equations Trin 5

5. Løs for variablen. For at gøre dette dividerer du venstre side af ligningen med -4 for at få x. Divider højre side af ligningen med -4 for at få -2.Så x = -2. Du har nu løst ligningen i to trin - subtraktion og division.

Metode 2 af 3: Løs ligninger med en variabel på hver side

Billede med titlen Solve Two Step Algebraic Equations Trin 6

1. Skriv opgaven. Problemet du vil arbejde på er følgende: -2x - 3 = 4x - 15. Før du fortsætter: Sørg for, at begge variabler er ens med hinanden. I dette tilfælde har -2x og 4x begge den samme variabel x, så du kan fortsætte.

Billede med titlen Solve Two Step Algebraic Equations Trin 7

2. Bring begge konstanter til højre side af ligningen. For at gøre dette skal du tilføje eller trække fra, så du kan fjerne konstanten i venstre side af ligningen. Konstanten er -3, så du skal bruge det modsatte, +3, og tilføje denne konstant til begge sider af ligningen.

Tilføjelse af +3 til venstre side af ligningen, -2x -3, giver (-2x -3) + 3 eller -2x til venstre.

Tilføjelse af +3 til højre side af ligningen, 4x -15, giver (4x - 15) +3 eller 4x -12.

Så (-2x - 3) +3 = (4x - 15) +3 = -2x = 4x - 12

Den nye ligning er -2x = 4x -12

Billede med titlen Solve Two Step Algebraic Equations Trin 8

3. Flyt variablerne til venstre side af ligningen. For at gøre dette skal du blot trække -4x fra begge sider af ligningen. Til venstre -2x - 4x = -6x, og til højre (4x -12) -4x = -12. Dette gør den nye ligning: -6x = -12

-2x - 4x = (4x - 12) - 4x = -6x = -12

Billede med titlen Solve Two Step Algebraic Equations Trin 9

4. Løs for variablen. Nu hvor du har forenklet ligningen til -6x = -12, skal du bare dividere begge sider af ligningen med -6 for at isolere variablen x, som ganges med -6. På venstre side af ligningen, -6x ÷ -6 = x, og på højre side, -12 ÷ -6 = 2. altså x = 2.

-6x -6 = -12 ÷ -6

x = 2

Metode 3 af 3: Andre måder at løse en to-trins ligning på

Billede med titlen Solve Two Step Algebraic Equations Trin 10

1. Løs ligninger i to trin, mens du holder variablen på højre side af ligningen.Så længe du isolerer variablen, får du det samme svar. Lad os tage et kig på det næste problem, 11 = 3 - 7x.For at løse dette er det første trin at kombinere kontanterne ved at trække 3 fra begge sider af ligningen. Så skal du dividere begge sider med -7 for at løse x. Nedenfor kan du se, hvordan det går:

11 = 3 - 7x =
11 - 3 = 3 - 3 - 7x =
8 = - 7x =
8/-7 = -7/7x
-8/7 = x eller -1.14 = x

Billede med titlen Solve Two Step Algebraic Equations Trin 11

2. Løs en to-trins ligning ved at gange i stedet for at dividere i slutningen. Princippet for at løse denne type ligninger er det samme: Kombiner konstanterne med hinanden og isoler variablen uden et led. Lad os tage følgende problem som eksempel, x/5 + 7 = -3. Den første ting at gøre er at trække 7 fra begge sider af ligningen og derefter gange begge sider med 5 for at løse x. Sådan kan du gøre det:

x/5 + 7 = -3 =

(x/5 + 7) - 7 = -3 - 7 =

x/5 = -10

x/5 * 5 = -10 * 5

x = -50

Tips

Hvis der ikke er et tal foran x, antag, at det er 1x.
Der er muligvis ingen konstant på begge sider af ligningen. Hvis der ikke er et tal efter x, antag, at følgende gælder: `x + 0`.