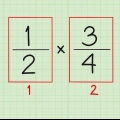
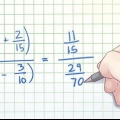
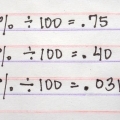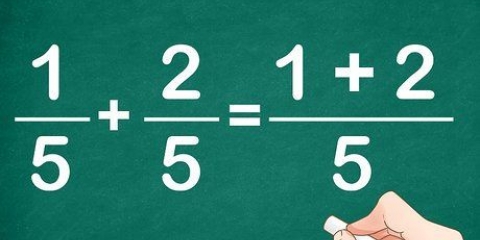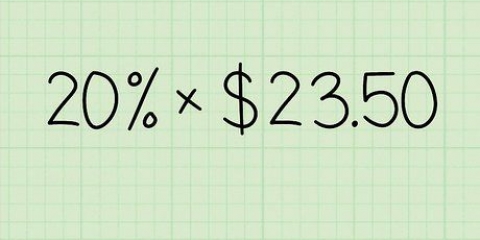Decimaler læses ofte på en måde, der viser deres lighed med brøken; For eksempel udtales 0,05 højt som "fem hundrededele", hvilket er det samme som 5/100. 

Hvis udbyttet er mindre end divisoren (eller i form af brøker, hvis tælleren er mindre end nævneren), så er tallet før decimaltegnet en 0. For eksempel, hvis du vil omregne brøken 3/4, bliver resultatet mindre end 1, så du får et 0 i kolonnen med enheder. Det samme gælder efter kommaet. Hvis tallet i tiendedele kolonnen (eller en anden kolonne efter det) er mindre end divisoren (igen nævneren i brøken), skal du tilføje et 0 til resultatet og fortsætte med at løse. 
Igen kan du tænke på brøken 3/4 som 3,0 ÷ 4, så du skriver det på den måde i din lange division. 
I tilfælde af 3/4 behandler du nu de 3 som 30. 4 går 7 gange i 30, og så står du tilbage med 2. Så det første tal i `tiendedele`-kolonnen bliver 7, og du tilføjer endnu et `0` til resten af 2, så du kan gentage processen igen. 4 går ind i 20 præcis 5 gange, så resultatet i decimal er 0,75. 


For eksempel er brøken 2/2 kun 1 (fordi 2 divideret med 2 er lig med 1). For at konvertere 1/5 til en brøk med nævneren 10 skal du gange med 2/2. Svaret er så 2/10. Du har måske lært, at du bør forenkle brøker så meget som muligt (især med lige tal). Dette er blot den omvendte proces, og det ændrer ikke værdien af brøken. 
For eksempel har du brøken 2/10. Nævneren har en 0. Så du skriver 2.0 for dette (dette ændrer ikke værdien) og flytter så decimaltegnet et sted til venstre. Du vil så få `0,2` som resultat. Prøv igen med dette nummer: 28/1000. Nævneren har tre nuller. Vi skriver nu `28` som `28.0`. Nu flytter vi decimaltegnet tre pladser til venstre, fordi tallet har tre nuller. Så resultatet er `0,028`. Du vil hurtigt opdage, at du kan gøre dette med alle slags tal, der har en nem nævner (eller en nævner, som du nemt kan lave).
Konverter brøker til decimaler
Indhold
Brøker og decimaler hører begge til sættet af rationelle tal. At konvertere brøker til decimaltal kan virke forvirrende i starten, men når du først forstår, hvad brøker faktisk er, bliver det meget lettere. Denne artikel forklarer først, hvad en brøk er, og derefter de forskellige måder at konvertere en brøk til et decimaltal.
Trin
Metode 1 af 3: Forståelse af brøker

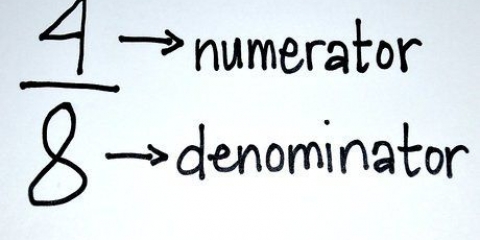
1. Prøv først at forstå, hvad en normalbrøk er. En brøk består af tre dele: den tæller, tallet over scorelinjen, selve scorelinjen og nævner, tallet under brøklinjen.
- Nævneren angiver, hvor mange lige store dele der er i en helhed. For eksempel: en pizza kan deles i 8 stykker. Nævneren for pizzaen er så `8`.
- Tælleren angiver det tal, der deles. En skive af hele pizzaen kan repræsenteres af en tæller på `1`. Divider fire med en `4` som en tæller.
- I dette eksempel spiste du et stykke af pizzaen. Hvis du spiste et stykke, kan det repræsenteres af 1/8 eller en af de 8 stykker. Har du spist tre stykker bliver det 3/8 mv.

2. Forstå decimaltallet. En decimal eller decimal, som navnet antyder, er baseret på tallet 10, ligesom decimalsystemet. Decimalbrøker bruger ikke en skillelinje til at angive, hvilken del af helheden der menes. I stedet er helheden baseret på 10, 100, 1000 osv. Brøken er repræsenteret af tallene til højre for decimaltegnet.

3. Forstå, at begge forestillinger faktisk er de samme. Brøker og decimaler er bare forskellige former for en værdi mindre end et helt tal. De forskellige former bruges afhængigt af de forskellige formål, folk har med at bruge dem. Vægt og størrelse er ofte udtrykt i brøker, men videnskabelige mål (der kræver større præcision) er næsten altid udtrykt i decimaler. Det faktum, at de kan bruges i flæng, betyder, at du ofte skal konvertere dem for at tilføje, trække fra eller sammenligne dem.
Metode 2 af 3: Konvertering af en brøk ved hjælp af lang division

1. Tænk på en brøk som en division. Den nemmeste måde at omregne en brøk til en decimal er at læse brøken som en divisionssum.
- 2/3 kan for eksempel også opfattes som 2 over 3; 5/8 er 5 divideret med 8; og 9/10 er det samme som 9 divideret med 10.
- En brøk er simpelthen resultatet af en divisionssum, når det tilbageværende ikke længere er et helt tal. Tælleren (toppen af brøken) bliver dividenden, nævneren (bunden af brøken) bliver divisor, og den decimal du får er resultatet.

2. Tænk på hvert ciffer som en del af en kolonne. For eksempel: Tallet 23,7 har et `2` i tiere-kolonnen, et `3` i et-kolonnen og efter decimaltegnet et `7` i den tiende kolonne (det vil sige, tallet så 7/10 er).

3. Tilføj et 0 til slutningen af tælleren. I lang division skal man trække divisor fra dividenden, og det er kun muligt, hvis dividenden er større end divisoren. Tilføj derefter et 0 til slutningen af divisoren, hvis du har et 0 efter decimalkommaet, som ikke har nogen effekt på resultatet.

4. Beregn hvor mange gange du kan gange divisoren for at komme så tæt på udbyttet som muligt.
Metode 3 af 3: Omregning af brøker med potenser 10 i nævneren

1. Kend de nævnere, der har magten 10 i sig. En "potens af 10" nævner er en nævner, der består af en hvilken som helst eksponent for tallet 10. Tallene 1000 eller 1000000 er potenser af 10, men i de fleste praktiske anvendelser af denne metode vil du have at gøre med tallene 10, 100 eller 1000.

2. Lær at genkende de letteste brøker at konvertere. Enhver brøk med 5 som nævner er en klar kandidat, men brøker med nævner 25 er også meget nemme at omregne.

3. Gang med 1. Som du sikkert ved, forbliver alle tal de samme, når du gange dem med 1. Men du kan også skrive 1 som en brøk.

4. Divider tælleren med nævneren. Du behøver ikke en svær lang division til dette. Alt du skal gøre er at behandle tælleren som hele tallet og derefter flytte decimaltegnet ét sted tilbage baseret på antallet af nuller i nævneren.
Tips
- Et andet ord for brøk er `brøk`, som kommer fra det latinske ord `frangere`. Dette betyder `brud`, og det er også grundlaget for ord som `brud` og `fragment`.
Artikler om emnet "Konverter brøker til decimaler"
Оцените, пожалуйста статью
Populær