I vores eksempel er nævneren for den stablede brøk (11/15)/(29/70) brøken 29/70. For at finde det omvendte vender vi det, og brøken bliver 70/29. Bemærk, at hvis den stablede brøk har et helt tal i nævneren, kan du behandle den som en brøk og stadig finde dens inverse. Antag for eksempel, at den stablede brøk var (11/15)/(29), så kan vi definere nævneren som 29/1, med den reciproke 1/29. 
I vores eksempel gange vi 11/15 × 70/29. 70 × 11 = 770 og 15 × 29 = 435. Det samme er vores nye simple fraktion 770/435. 
En fælles divisor på 770 og 435 er 5. Så hvis vi dividerer tælleren og nævneren af vores brøk med 5, får vi 154/87. 154 og 87 har ingen fælles faktorer, så vi ved, at vi har fundet det endelige svar! 

Dette er lettere at forstå med et eksempel. Lad os prøve at forenkle den stablede fraktion, vi nævnte ovenfor, (((1)/(x+3)) + x - 10)/(x +4 +((1)/(x - 5))). Brøkleddene i denne sammensatte fraktion er (1)/(x+3) og (1)/(x-5). Fællesnævneren for disse to brøker er produktet af deres nævnere: (x+3)(x-5). 
I vores eksempel gange vi den stablede brøk (((1)/(x+3)) + x - 10)/(x +4 +((1)/(x - 5))), med ((x+) 3 )(x-5))/((x+3)(x-5)). Vi bliver nødt til at gange med tælleren og nævneren af den stablede brøk, og gange hvert led med (x+3)(x-5). Lad os først gange tælleren: (((1)/(x+3)) + x - 10) × (x+3)(x-5) = (((x+3)(x-5)/(x+3)) + x((x+3)(x-5)) - 10((x+3)(x-5)) = (x-5) + (x(x - 2x - 15)) - (10(x - 2x - 15)) = (x-5) + (x - 2x - 15x) - (10x - 20x - 150) = (x-5) + x - 12x + 5x + 150 = x - 12x + 6x + 145 
Nævneren af vores stablede brøk, (((1)/(x+3)) + x - 10)/(x +4 +((1)/(x - 5))), er x +4 +(( 1)/(x-5)). Vi skal gange dette med kgd vi fandt, (x+3)(x-5). (x +4 +((1)/(x - 5))) × (x+3)(x-5) = x((x+3)(x-5)) + 4((x+3)(x-5)) + (1/(x-5))(x+3)(x-5). = x(x - 2x - 15) + 4(x - 2x - 15) + ((x+3)(x-5))/(x-5) = x - 2x - 15x + 4x - 8x - 60 + (x+3) = x + 2x - 23x - 60 + (x+3) = x + 2x - 22x - 57 
Ved at bruge tælleren og nævneren, vi fandt ovenfor, kan vi konstruere en brøk, der er lig med vores oprindelige stablede brøk, men som ikke indeholder brøker. Tælleren vi fik var x - 12x + 6x + 145 og nævneren var x + 2x - 22x - 57, så den nye brøk er: (x - 12x + 6x + 145)/(x + 2x - 22x - 57)
Forenkle stablede brøker
Indhold
Stablede brøker er dem, hvor tælleren, nævneren eller begge indeholder brøker selv. Af denne grund kan du også kalde dette `brøker i brøker`. Forenkling af stablede brøker er en proces, der kan variere fra let til svær baseret på, hvor mange led der er til stede i tælleren og nævneren, om nogen af termerne er variable, og i givet fald kompleksiteten af de variable led. Se trin 1 nedenfor for at komme i gang!
Trin
Metode 1 af 2: Simplificering af stablede brøker med omvendt multiplikation

1. Om nødvendigt forenkles tælleren og nævneren til nogle få brøker. Stablede brøker er ikke nødvendigvis svære at løse. Faktisk er stablede brøker, hvor tælleren og nævneren begge indeholder en enkelt brøk, normalt ret nemme at løse. Så hvis tælleren eller nævneren af din stablede brøk (eller begge dele) indeholder flere brøker eller brøker og hele tal, forenkles som ønsket for at få en enkelt brøk i både tæller og nævner. Dette kan kræve det mindste fælles multiplum (LCM) at finde to eller flere brøker.
- Antag, at vi ønsker at forenkle den komplekse brøk (3/5 + 2/15)/(5/7 - 3/10). Først kan vi så simplificere både tælleren og nævneren af vores komplekse brøk til enkelte brøker.
- For at forenkle tælleren, lad os tage en LCF på 15 ved at gange 3/5 med 3/3. Vores tæller bliver 9/15 + 2/15, hvilket er lig med 11/15.
- For at forenkle nævneren, lad os tage en lcm på 70 ved at gange 5/7 med 10/10 og 3/10 med 7/7. Vores nævner vil være 50/70 - 21/70, hvilket er lig med 29/70.
- Så vores nye stablede fraktion er (11/15)/(29/70).

2. Vend nævneren og find det omvendte. Per definition, dele fra et nummer til et andet det samme som gange det første tal med det gensidige af det andet tal. Nu hvor vi har fået en stablet brøk med en enkelt brøk i både tæller og nævner, kan vi bruge denne divisionsegenskab til at simplificere vores stablede brøk! Find først det reciproke af nævneren af den stablede brøk. Gør dette ved at `invertere` brøken -- tælleren erstatter nævneren og omvendt.

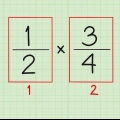
3. Multiplicer tælleren for den stablede brøk med den reciproke af nævneren. Nu hvor du har opnået den reciproke af nævneren af din stablede brøk, skal du gange den med tælleren for at få en enkelt enkel brøk! Husk, at for at gange to brøker, multiplicerer vi ikke på kryds og tværs -- tælleren i den nye brøk er produktet af tælleren af de to gamle, og det samme gør nævneren.

4. Forenkle den nye brøk ved at finde den største fælles divisor. Vi har nu en enkelt, simpel brøk, så det eneste, der er tilbage, er at repræsentere det i de enklest mulige termer. Særlig største fælles divisor (gcd) af tælleren og nævneren og divider begge med dette tal for at forenkle.
Metode 2 af 2: Simplificering af stablede brøker med variable termer

1. Når det er muligt, skal du bruge den inverse multiplikationsmetode som beskrevet ovenfor. For at være klar, kan næsten enhver stablet brøk forenkles ved at reducere tælleren og nævneren til enkelte brøker og gange tælleren med den reciproke af nævneren. Stablede fraktioner af variable er ingen undtagelse, men jo mere komplicerede variabeludtrykkene i den stablede fraktion er, jo sværere og mere tidskrævende er det at udføre omvendt multiplikation. For `simple` stablede brøker med variable er multiplikation med det omvendte et godt valg, men stablede brøker med flere variabelled i tælleren og nævneren kan være lettere at forenkle ved hjælp af den alternative metode beskrevet nedenfor.
- For eksempel: (1/x)/(x/6) er let at forenkle med invers multiplikation. 1/x × 6/x = `6/x. Det er ikke nødvendigt at bruge en alternativ metode.
- Brøken (((1)/(x+3)) + x - 10)/(x +4 +((1)/(x - 5))) er dog sværere at forenkle med omvendt multiplikation. At reducere tælleren og nævneren af denne stablede brøk til enkelte brøker, gange omvendt og reducere resultatet til de enkleste led, er sandsynligvis en kompliceret proces. I dette tilfælde kan den alternative metode nedenfor være lettere.

2. Hvis invers multiplikation er upraktisk, start med at finde den mindste fælles divisor af divisionsleddene i den stablede brøk. Det første trin i denne alternative metode til forenkling er at finde kgd af alle brøkled i den stablede brøk -- både i tælleren og i nævneren. Hvis en eller flere af brøkleddene har variable i deres nævnere, er kgd blot produktet af deres nævnere.

3. Multiplicer tælleren for den stablede brøk med det kgd. Dernæst skal vi gange vilkårene i vores stablede brøk med kgd af dens brøkled. Med andre ord vil vi gange hele den stablede brøk med (kgd)/(kgd). Vi kan gøre dette simpelthen fordi (kgd)/(kgd) er lig med 1. Gang først tælleren med sig selv.

4. Multiplicer nævneren af den stablede brøk med kgd, som du gjorde med tælleren. Gang den stablede brøk med den kgd, du fandt, ved at gå til nævneren. Gang hvert led med kgd.

5. Dann en ny, forenklet brøk fra den tæller og nævner, du lige har fundet. Efter at have ganget din brøk med dit (kgd)/(kgd) udtryk og forenklet det ved at strege ens udtryk, skal du stå tilbage med en simpel brøk, der ikke indeholder brøkled. Som du måske har bemærket, ophæver nævnerne af disse brøker hinanden (ved at gange brøkerne i den oprindelige stablede brøk med kgd), hvilket efterlader variable led og heltal i tælleren og nævneren af dit svar, men ikke brøker.
Tips
- Vis hvert trin i dit arbejde. Brøker kan være forvirrende, hvis du vil gå for hurtigt eller forsøge at få dem ud af dit hoved.
- Se efter eksempler på stablede brøker online eller i din lærebog. Følg hvert trin, indtil du mestrer det.
Artikler om emnet "Forenkle stablede brøker"
Оцените, пожалуйста статью
Populær