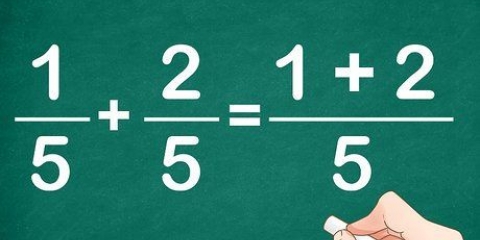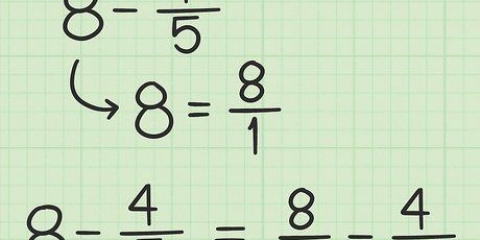18 ÷ 3 = 6, så 2/3 = (2x6)/(3x6)=12/18 18 ÷ 6 = 3, så 5/6 = (5x3)/(6x3)=15/18 18 ÷ 3 = 6, så 1/3 = (1x6)/(3x6)=6/18 

6/18 = (6 6)/(18 ÷ 6) = 1/3 12/18 = (12 6)/(18 ÷ 6) = 2/3 15/18 = (15 3)/(18 ÷ 3) = 5/6 Svaret er "1/3, 2/3, 5/6" 

Dette kaldes krydsmultiplikation, fordi du multiplicerer tal diagonalt. 



Husk altid at placere produktet af multiplikationen ud for den brøk, hvis tæller du brugte. 
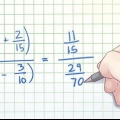
3/5=(3x3)/(5x3)=9/15 2/3=(2x5)/(3x5)=10/15 9/15 er mindre end 10/15 Så 3/5 er mindre end 2/3 

8/3 = 2 + 2/3 9/9 = 1 19/4 = 4 + 3/4 13/6 = 2 + 1/6 
1 er den mindste 2 + 2/3 og 2 + 1/6 (vi ved ikke, hvilken der er større end den anden endnu) 4 + 3/4 er den største 
2/3 = (2x2)/(3x2) = 4/6 1/6 = 1/6 4/6 er større end 1/6 2 + 4/6 er større end 2 + 1/6 2 + 2/3 er større end 2 + 1/6 

Sorter brøker efter størrelse
Indhold
Selvom det er nemt at ordne heltal som 1, 3 og 8 efter størrelse, er det ikke altid indlysende med brøker. Hvis hver nævner er lige, kan du bestille dem ligesom heltal, f.eks. 1/5, 3/5 og 8/5. I andre tilfælde kan du konvertere brøkerne, så de har samme nævner, uden at ændre brøkens værdi. Dette bliver nemmere med øvelse, og du kan bruge nogle praktiske tricks, både når du sammenligner to brøker eller når du bestiller brøker, hvor tælleren er større end nævneren, de uægte brøker såsom 7/3.
Trin
Metode 1 af 3: Bestilling af et vilkårligt antal brøker

1. Find en lige nævner for alle brøker. Brug en af følgende metoder til at finde en nævner, eller reducer antallet af en brøk, som du kan bruge til at omskrive hver brøk på listen for nem sammenligning. Det er det, du kalder a fællesnævner, eller den mindste fællesnævner hvis dette er det mindst mulige:
- Gang hver nævner sammen. Hvis du f.eks. sammenligner 2/3, 5/6 og 1/3, skal du gange disse nævnere sammen: 3 x 6 = 18. Dette er en simpel metode, men en, der ofte resulterer i et meget større antal end de andre metoder, som er lidt vanskeligere.
- Eller angiv multipla af hver nævner i en separat kolonne, indtil et tal, der forekommer oftere, skiller sig ud. For eksempel, ved 2/3, 5/6 og 1/3 har du listemultipler af 3:3, 6, 9, 12, 15, 18. Derefter en liste over multipla af 6: 6, 12, 18. Fordi 18 forekommer i begge lister, brug det tal (Du kan også bruge 12, men eksemplerne nedenfor antager, at du bruger 18).

2. Konverter hver brøk, så de har en ens nævner. Husk, at hvis du multiplicerer tælleren og nævneren af en brøk med det samme tal, forbliver værdien af brøken den samme. Brug denne teknik med hver brøk, en ad gangen, så hver brøk har den samme nævner. Prøv dette for 2/3, 5/6 og 1/3 med nævneren 18:

3. Ordne brøkerne efter tællere. Nu hvor alle brøker har den samme nævner, er de nemme at sammenligne. Bestil dem fra mindste til største i henhold til tælleren. Dette giver os følgende liste: 18/6, 18/12, 15/18.

4. Returner hver brøk til dens oprindelige form. Lad brøkerne stå i denne rækkefølge, men konverter dem tilbage til den oprindelige brøk. Det gør du ved blot at huske hvilken brøk der hører til hvilken eller ved at dividere brøkens øverste og nederste tal igen:
Metode 2 af 3: Ordning af to brøker med krydsmultiplikation

1. Skriv de to brøker side om side. Sammenlign for eksempel brøken 3/5 og brøken 2/3. Skriv disse side om side: 3/5 til venstre og 2/3 til højre.

2. Gang tælleren for den første brøk med nævneren af den anden. Altså: 3 x 3 = 9.

3. Skriv dit svar ud for den første brøk. Skriv produktet af 3 x 3 = 9 ved siden af den første brøk.

4. Gang tælleren af anden brøk med nævneren af først. For at se, hvilken der er størst, sammenligner vi svaret med en anden multiplikation. Gang disse to tal sammen. I dette eksempel (vi sammenligner 3/5 og 2/3), multiplicerer vi 2 x 5.

5. Skriv svaret ud for den anden brøk. Skriv resultatet af 2 x 5 =10 ud for den anden brøk.

6. Sammenlign værdierne af resultaterne. Hvis den ene værdi er større end den anden, er brøken ved siden af resultatet også den største. Så da 9 er mindre end 10, er 3/5 mindre end 2/3.

7. Hvordan fungerer dette præcist? Det du gør er at konvertere brøkerne, så de begge har samme nævner. Så dette er hvad krydsmultiplikation faktisk gør! Det springer faktisk over at skrive nævnerne ned, fordi i tilfælde af ens nævnere behøver du kun at sammenligne tællere. Så som følger, uden den korte rute for krydsmultiplikation:
Metode 3 af 3: Bestilling af brøker større end én

1. Brug denne metode til brøker, hvor tælleren er større end nævneren. Hvis tælleren er større end nævneren, så er denne brøk større end 1. 8/3 er et eksempel på dette. Du kan også bruge dette til brøker med samme tæller og nævner, såsom 9/9. Disse er begge eksempler på "upassende" brøker.
- Du kan stadig bruge de andre metoder til disse fraktioner. Denne metode hjælper dig med at forstå disse brøker bedre og kan være en smule hurtigere.

2. Konverter enhver uægte fraktion til en blandet fraktion. Gør det til en kombination af et heltal og en brøk. Nogle gange kan du sagtens gøre dette udenad. For eksempel, 9/9 = 1. I de vanskeligere tilfælde skal du bruge lang division for at finde ud af, hvor mange gange nævneren er delelig med tælleren. Enhver rest af den lange division forbliver som en brøkdel. For eksempel:

3. Sorter de blandede tal efter hele tallet. Nu hvor der ikke er flere uægte brøker, har du en bedre idé om størrelsen af hvert tal. Ignorer først brøkerne og sorter hvert blandet tal efter heltal:

4. Sammenlign om nødvendigt brøkerne i hver gruppe. Hvis du har flere blandede tal med det samme heltal, såsom 2 + 2/3 og 2 + 1/6, skal du sammenligne brøkdelen af begge tal for at finde ud af, hvilken der er størst. I eksemplet sammenligner vi 2 + 2/3 og 2 + 1/6 og konverterer brøkerne til samme nævner:

5. Brug resultatet til yderligere at sortere listen over blandede tal. Rækkefølgen af hele listen bliver nu: 1, 2 + 1/6, 2 + 2/3, 4 + 3/4.

6. Konverter de blandede tal tilbage til de oprindelige brøker. Hold rækkefølgen den samme, men fortryd eventuelle ændringer og omskriv brøkerne som de originale uægte brøker: 9/9, 8/3, 13/6, 19/4.
Tips
- Ved sekventering af et stort antal fraktioner kan det være nyttigt at sammenligne små grupper på 2, 3 eller 4 fraktioner.
- Selvom det kan være nyttigt at finde den mindste fællesnævner, vil enhver fællesnævner fungere. Prøv at placere 2/3, 5/6 og 1/3 med en fællesnævner på 36 og se om du får det samme resultat.
- Hvis tællerne alle er ens, kan du også hurtigt bestille brøkerne. For eksempel 1/8 < 1/7 < 1/6 < 1/5. Tænk på det, som om det var en pizza: hvis du går fra 1/2 til 1/8, skærer du pizzaen i 8 stykker i stedet for 2, og stykkerne er mindre.
Artikler om emnet "Sorter brøker efter størrelse"
Оцените, пожалуйста статью
Populær