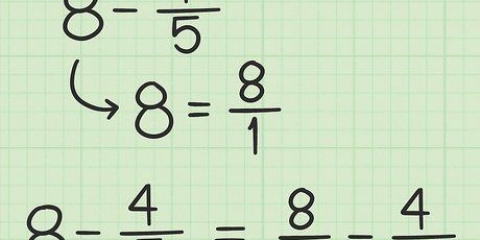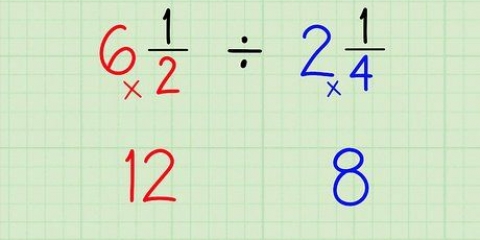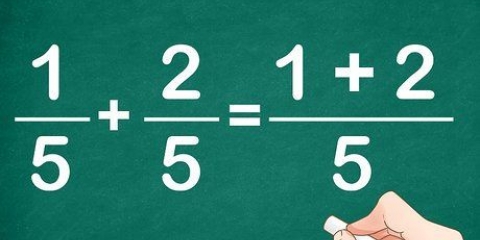Angiv de første par multipla af 4:4 x 1 = 4, 4 x 2 = 8, 4 x 3 = 12, 4 x 4 =16 Angiv de første par multipla af 3:3 x 1 = 3, 3 x 2 = 6, 3 x 3 = 9, 3 x 4 = 12 Stop så snart du finder et fælles multiplum. Du kan se, at 12 er et multiplum af både 4 og 3. Fordi dette er det mindste antal, du kan stoppe her. Bemærk, at du kan gøre dette for alle typer tal, inklusive heltal og blandede brøker. For de heltal skal du forestille dig, at nævneren er 1. (Altså 2 = 2/1.) For blandede brøker, omskriv det som en uægte brøk. (Altså 2 1/2 = 5/2.) 
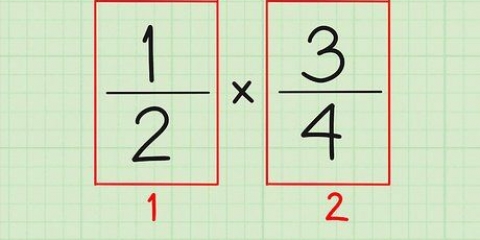
For brøken 3/4 ved du, at nævneren skal være 12, så du skal finde det tal, der ganget med 4 giver tallet 12. 4 x 3 = 12, så gang 3/4 med 3/3, så tæller og nævner forbliver i det rigtige forhold. 3/4 kan derfor omskrives til 9/12. For brøken 1/3 ved du, at nævneren skal være 12, så du skal finde det tal, der ganget med 4 giver tallet 12. 4 x 3 = 12, så gang 1/3 med 4/4, så tæller og nævner forbliver i det rigtige forhold. 1/4 kan derfor omskrives til 4/12. 
3/4 - 1/3 = 9/12 - 4/12 9/12 - 4/12 = (9-4)/12 
9-4 = 5, så 9/12 - 4/12 = 5/12 
For eksempel kan brøken 6/8 forenkles, fordi både 6 og 8 er delelige med 2. Det forenklede svar bliver så: 6/2 = 3, 8/2 = 4, så 6/8 = 3/4.
Træk brøker fra
Det er let at trække brøker med de samme nævnere, men ulige nævnere kan tage en række forskellige trin for at gøre nævnerne lige, så de let kan trækkes fra hinanden. Disse trin tager lidt mere tid, men hvis du bliver fortrolig med dem, vil du være i stand til at trække brøker fra på ingen tid. Hvis du vil vide, hvordan du gør dette, skal du følge disse trin.
Trin

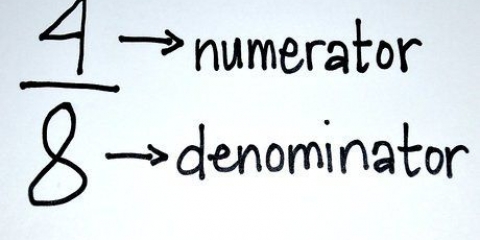
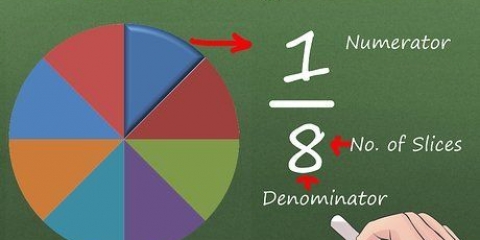
1. Find nævnerne for brøkerne. Hvis du vil trække brøker fra hinanden, skal du først sørge for, at de har samme nævner. Tælleren er tallet over scorelinjen, og nævneren er tallet under scorelinjen. I eksemplet, 3/4 - 1/3, er brøkens to nævnere 4 og 3. ring om dem.
- Hvis nævnerne af brøkerne er de samme, kan du bare trække tællerne fra hinanden og lade nævneren være den samme. Som et eksempel, 4/5 - 3/5 = 1/5. Hvis brøken er forenklet på denne måde, er du færdig med det samme.

2. Find det mindste fælles multiplum (LCM) af nævnerne. Lcm af to tal er det mindste tal, der er deleligt med begge nævnere. Du skal finde kgv på 4 og 3 her. Dette giver dig den mindste fællesnævner for brøken. Her er en god metode, du kan bruge, når det kommer til små tal:

3. Sørg for, at brøkernes tællere ændres med det. Nu hvor du ved, at lcm af 4 og 3 er lig med 12, tag dette tal som den nye nævner af brøkerne. Men for at gøre brøkerne ækvivalente, skal du gange tællerne med et tal, der sikrer, at tæller og nævner igen står i det rigtige forhold. Sådan gør du det:

4. Skriv de nye tællere over den laveste fællesnævner. Nu hvor du ved, at det mindste fælles multiplum af 4 og 3 er lig med 12, er det muligt at sige, at den mindste fællesnævner af brøkerne 1/3 og 3/4 er lig med 12. Nu hvor du også kender de nye tællere, kan du bare skrive dem over nævneren som én brøk, med tællere trukket fra hinanden. Sørg for at skrive tællerne i den rigtige rækkefølge, ellers får du et forkert svar.Sådan afmelder du dig:

5. Træk tællere fra. Når du har placeret de nye tællere over fællesnævneren, kan du trække dem fra hinanden.

6. Forenkle dit svar. Har du fundet svaret, så tjek det og forenkle, hvis det er muligt. Hvis tælleren og nævneren kan divideres med det samme tal, skal du gøre dette. Husk at brøker angiver et forhold, så hvad du gør med nævneren, gør det samme med tælleren. Divider ikke et tal uden at dividere det andet med det samme tal. 5/12 forbliver som den er, fordi den ikke kan forenkles yderligere.
Artikler om emnet "Træk brøker fra"
Оцените, пожалуйста статью
Populær