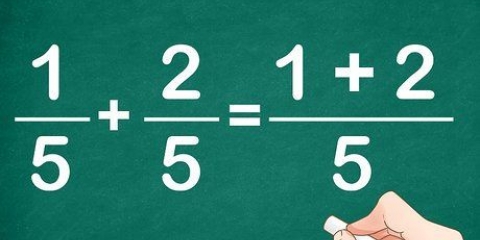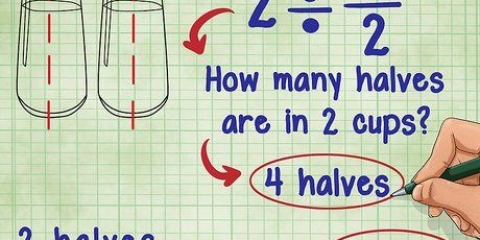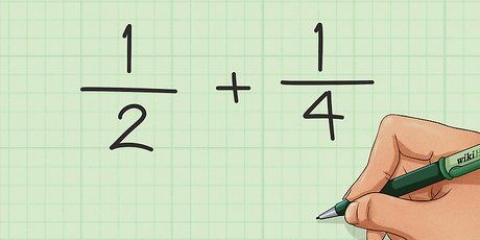Så antag at vi har 1/2 x 3/4, så multiplicerer vi som følger: 1 x 3 og 2 x 4.Svaret er så 3/8. 


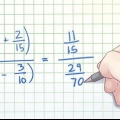
Hvis problemet var 8/15 ÷ 3/4, vil dette nu være 8/15 x 4/3. 
8 x 4 = 32 og 15 x 3 = 45, så svaret er 32/45. 

I vores eksempel bliver dette: 3 x 5 = 15.

I vores eksempel: 15 + 2 = 17 
I vores tilfælde bliver dette: 17/5. 

Bestem, hvor mange gange den aktuelle nævner går ind i det mindste fælles multiplum. For 1/4, 4 x 3 = 12. For 1/6, 6 x 2 = 12. Multipliceret tælleren og nævneren af brøken med det tal. For ¼ gange du både 1 og 4 med 3, hvilket resulterer i 3/12. 1/6 x 2 = 2/12. Nu ser dette udsagn sådan her ud: 3/12 + 2/12 eller 3/12 - 2/12. 
Så for 3/12 + 2/12 er svaret 5/12. For 3/12 - 2/12 er det 1/12 Konverter blandede brøker til uægte brøker, før du starter. Spørg din lærer, om du skal forenkle svarene. For eksempel kan 2/5 ikke forenkles yderligere, men 16/40 kan.
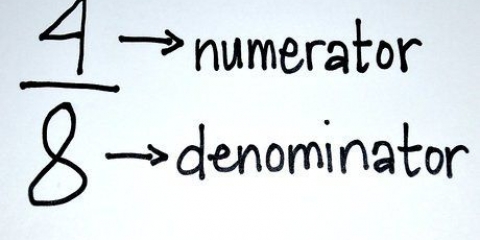
Løse brøker
Indhold
Brøker virker nogle gange lidt svære at løse, men med lidt øvelse og lidt ekstra viden bliver dette meget nemmere. Når du har forstået det grundlæggende, vil du opdage, at løsning af brøker faktisk er et stykke kage.
Trin
Metode 1 af 4: Multiplicering af brøker

1. Sørg for, at du har at gøre med to brøker. Disse instruktioner virker kun med to brøker.Hvis du har at gøre med en blandet brøk, skal du først konvertere den til en uægte brøk...

2. Gang tæller 1 med tæller 2, og gang nævner 1 med nævner 2.
Metode 2 af 4: Opdeling af brøker

1. Sørg for, at du har at gøre med to brøker. Igen fungerer denne proces KUN, hvis du har konverteret eventuelle blandede brøker til ukorrekte brøker.

2. Vend den anden brøk om. Det er lige meget hvilken brøk, så længe du ikke vender begge brøker.

3. Skift divisionstegnet til en multiplikation.

4. Gang begge tællere og begge nævnere.
Metode 3 af 4: Konvertering af blandede fraktioner til ukorrekte fraktioner

1. Konverter blandede brøker til uægte brøker. Uægte brøker er de brøker, hvis tæller er større end nævneren.(For eksempel 17/5.)Hvis du multiplicerer og dividerer, skal du konvertere blandede brøker til uægte brøker, før du fortsætter med at løse problemet.
- Antag, at du har den blandede fraktion 3 2/5.

2. Tag hele tallet (tallet før brøken) og gang det med nævneren.


3. Føj det svar til tælleren.

4. Placer dette tal som en ny tæller over brøklinjen, og du har en uægte brøk.
Metode 4 af 4: Tilføjelse og subtrahering af brøker

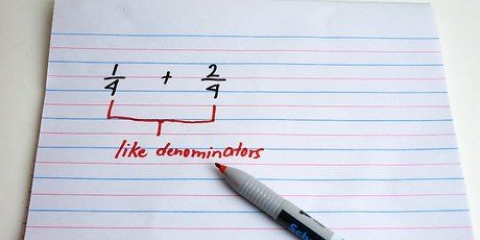
1. Find det mindste fælles multiplum af nævnerne (det nederste tal). For både at lægge til og trække brøker fra, starter du med det samme. Find det mindste tal, der passer til begge nævnere.
- For eksempel, hvis du tager brøkerne 1/4 og 1/6, er det mindste fælles multiplum 12. (4x3=12, 6x2=12)

2. Gang brøkerne afhængigt af det mindste fælles multiplum. Husk, du ændrer ikke brøken, bare hvordan den udtrykkes. Tænk på en pizza - 1/2 eller 2/4 af en pizza er den samme mængde pizza, bare udtrykt anderledes.

3. Tilføj eller subtraher de to tællere (øverste tal), men IKKE nævnerne.Dette er ikke tilladt, fordi du ønsker at beregne, hvor meget af denne brøkdel, du har i alt. Tager man også nævnerne med, ændres brøkerne.
Tips
- Sørg for at mestre de grundlæggende matematiske færdigheder (addition, subtraktion, multiplikation og division) godt, så udregningerne ikke tager unødigt lang tid og er svære.
- Den reciproke af et heltal er at placere dette tal som nævneren i en brøk, med et 1 som tæller. For eksempel bliver 5 så til 1/5.
- Du kan gange og dividere blandede brøker uden først at konvertere dem til uægte brøker. Men så har du brug for andre matematiske færdigheder, og regnestykket bliver meget mere komplekst. Så det er generelt bedre at følge ruten for ukorrekte fraktioner.
- Husk: At dividere er det samme som at gange med det gensidige.
- Når du tager det omvendte af et negativt tal, forbliver minustegnet i tælleren.
Advarsler
- Spørg din lærer, om du skal konvertere uægte brøker til blandede brøker.
- For eksempel 3 1/4 i stedet for 13/4.
Artikler om emnet "Løse brøker"
Оцените, пожалуйста статью
Populær