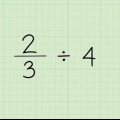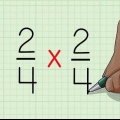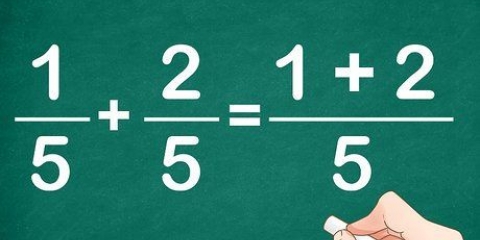Den gensidige 3/4 er 4/3. Den gensidige 7/5 er 5/7. Den gensidige af 1/2 er 2/1 og derfor 2. 
Lad tælleren være uændret. Gør divisionstegnet til en multiplikation. Lav det omvendte af den anden brøk. Gang tællerne af de to brøker. Resultatet vil være tælleren for dit svar. Gang nævnerne af de to brøker. Resultatet vil være nævneren for dit svar. Forenkle brøken. 
1/3 ÷ 2/5 = bliver til: 1/3 * __ = Nu roterer vi den anden brøk (2/5). Dette bliver så 5/2: 1/3 * 5/2 = Nu gange vi tællerne for de to brøker, 1*5 = 5. 1/3 * 5/2 = 5/ Nu gange vi nævnerne af de to brøker, 3*2 = 6. Vi har nu: 1/3 * 5/2 = 5/6 Denne særlige fraktion kan ikke forenkles yderligere, så vi har nu vores svar. 



2/3 * 7/3 = __ 

Del tælleren først 14 ved hjælp af 9.9 går ind i 14 én gang, med en rest på 5, så du kan skrive dette som: 1 5/9. Du kan stoppe nu, for du har fundet svaret! Du kan se, at denne brøk ikke kan forenkles yderligere, fordi 9 ikke er fuldt deleligt med 5, og fordi tælleren er et primtal. 
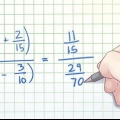
Divider først tælleren med nævneren, (24/10 = 2 resterende 4). Skriv svaret som 2 4/10. Men vi kan forenkle denne brøk endnu mere! Bemærk, at 4 og 10 begge er lige tal, så det første trin er at forenkle ved at dividere dem begge med 2.Brøken er nu 2/5. Fordi nævneren (5) ikke passer helt ind i tælleren (2), og også er primtal, ved du, at du ikke kan forenkle denne brøk yderligere. Så svaret er: 2 2/5. 
At dividere brøker med brøker
Indhold
At dividere en brøk med en brøk kan virke forvirrende i starten, men det er faktisk meget simpelt. Alt du skal gøre er at vende den nederste eller anden brøk og derefter gange begge brøker sammen! Denne artikel vil vise dig, hvordan du gør dette, og vil vise dig, at dividere brøker med brøker overhovedet ikke burde være et problem.
Trin
Del 1 af 2: Forstå, hvordan det virker

1. Tænk på, hvad det betyder at dividere med en brøk.Øvelsen 2 ÷ 1/2 siger det samme som: ”Hvor mange gange går ½ i 2?”Svaret er 4, for man kan dele 2 i 4 halve stykker.
- Prøv også at tænke over dette problem i forhold til glas vand: Hvor mange halve glas vand er der i 2 glas vand?? Det kan du løse ved at hælde 2 halve glas vand i et andet glas, så du til sidst har 2 hele glas vand: 2 halve/1 glas * 2 glas = 4 halve glas.
- Det betyder, at hvis du dividerer et tal med et tal mellem 0 og 1, vil svaret altid være større end det tal! Dette gælder uanset om du dividerer et helt tal eller en brøk med en anden brøk.

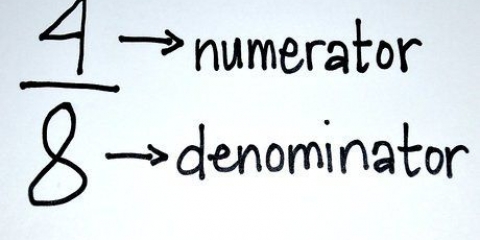
2. Division er det modsatte af multiplikation.Så du kan også tænke på at dividere med en brøk som at gange med den reciproke af den brøk.Det omvendte af en brøk er, hvad den siger, blot at bytte tæller og nævner. Om et øjeblik skal vi dividere brøker med brøker ved at gange med den reciproke af nævneren, men for nu vil vi se på nogle invers af brøker:

3. Husk følgende trin for at dividere en brøk med en anden brøk.Her er trinene i rækkefølge:

4. Gennemfør disse trin i eksemplet 1/3 ÷ 2/5.Vi lader tælleren (den første brøk) være uændret og ændrer divisionstegnet til et tidstegn:

5. Prøv at huske følgende:"At dividere med en brøk er det samme som at gange med det reciproke."
Del 2 af 2: At dividere brøker med brøker - eksempler

1. Start med et eksempelproblem. Antag, at vi har opgaven 2/3 3/7. Spørgsmålet her er, hvor ofte 3/7 passer ind i 2/3. Gå ikke i panik; det er ikke så svært, som det lyder!

2. Gør divisionstegnet til et multiplikationstegn. Opgaven bliver nu: 2/3 * __ (vi udfylder det tomme felt om et øjeblik.)

3. Nu bestemmer vi den gensidige af den anden fraktion.Det betyder, at vi vender 3/7, så tælleren bliver 3 og nævneren bliver 7.Den gensidige 3/7 er 7/3.Nu skriver vi det nye problem ned:

4. Gang brøkerne.Først gange vi tællerne for de to brøker: 2 * 7 = 14.14 er tælleren for dit svar.Derefter gange vi nævnerne af de to brøker sammen:3 * 3 = 9.9 er nævneren for dit svar.Nu ved du det 2/3 * 7/3 = 14/9.

5. Forenkle brøken.I dette tilfælde, fordi brøkens tæller er større end nævneren, ved vi, at brøken er større end 1, og vi skal konvertere den til et blandet tal.(Et blandet tal er et heltal med en brøk, såsom 1 2/3.)

6. Lad os prøve et andet eksempel!Antag, at vi har følgende problem 4/5 2/6 =.Først skal du ændre divisionstegnet til et multiplikationstegn (4/5 * __ =), så find den gensidige af 2/6, som er 6/2.Nu er opgaven som følger: 4/5 * 6/2 =__.Nu gange vi tællerne, 4 * 6 = 24, og nævnerne 5* 2 = 10.Nu har vi følgende:4/5 * 6/2 = 24/10.Forenkle brøken. Da tælleren er større end nævneren, bliver vi nødt til at konvertere denne til en blandet brøk.

7. Få mere at vide om at forenkle brøker. Du har måske lært alt det én gang, men det skader aldrig at genopfriske al den tabte viden igen. Forskellige artikler kan findes på internettet for at forbedre disse færdigheder igen.
Artikler om emnet "At dividere brøker med brøker"
Оцените, пожалуйста статью
Populær