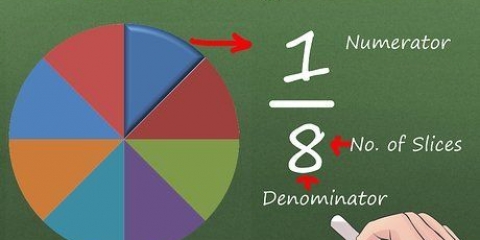
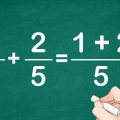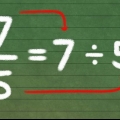Eks. 1: 1/4 + 2/4
Eks. 2: 3/8 + 2/8 + 4/8
Eks. 1: 1/4 + 2/4 er vores ligning. "1" og"2" er tællerne. Det betyder 1 + 2 = 3.
Eks. 2: 3/8 + 2/8 + 4/8 er vores ligning. "3" og"2" og"4" er tællerne. Det betyder 3 + 2 + 4 = 9.
Eks. 1: 3 er vores nye tæller, og 4 er den `nye` nævner. Dette giver svaret: 3/4. 1/4 + 2/4 = 3/4.
Eks. 2: 9 er vores nye tæller, og 8 er den `nye` nævner. Dette giver svaret: 9/8. 3/8 + 2/8 + 4/8 = 9/8.
Hvis tælleren er større end nævneren, som i for eksempel. 2, så kan mindst ét helt tal fjernes fra brøken. Divider tælleren med nævneren. Hvis vi dividerer 9 med 8, får vi 1 heltal og resten af 1. Sæt hele tallet før brøken og resten som tæller for den nye brøk, og hold nævneren den samme.9/8 = 1 1/8.

Eks. 3: 1/3 + 3/5
Eks. 4: 2/7 + 2/14
Eks. 3: 3 x 5 = 15. Begge brøker har 8 som nævner.
Eks. 4: 14 er et multiplum af 7. Så vi skal bare gange 7 med 2 for at få 14. Begge brøker har da en nævner på 14.
Eks. 3: 1/3 x 5/5 = 5/15.
Eks. 4: For denne brøk skal vi bare gange den første brøk med 2, for på denne måde kan vi få fællesnævneren.
2/7 x 2/2 = 4/14. Eks. 3: 3/5 x 3/3 = 9/15.
Eks. 4: Den anden brøk skal ikke ganges, fordi begge brøker allerede har den samme nævner. Eks. 3: i stedet for 1/3 + 3/5, har vi 5/15 + 9/15
Eks. 4: i stedet for 2/7 + 2/14, har vi 4/14 + 2/14
Eks. 3: 5 + 9 = 14. 14 bliver den nye tæller.
Eks. 4: 4 + 2 = 6. 6 bliver den nye tæller.
Eks. 3: 15 bliver vores nye nævner.
Eks. 4: 14 bliver vores nye nævner.
Eks. 3: 14/15 er vores nye svar på 1/3 + 3/5 = ?
Eks. 4: 6/14 er vores svar på 2/7 + 2/14 = ?
Eks. 3: 14/15 kan ikke forenkles.
Eks. 4: 6/14 kan reduceres til 3/7 ved at dividere både tælleren og nævneren med 2, den største fælles divisor.
Læg brøker sammen
Indhold
At kunne tilføje brøker er en meget nyttig færdighed. Ikke kun for folkeskolen og gymnasiet, det er bare en meget praktisk færdighed. Læs mere om at tilføje brøker her. Du vil blive overrasket over, hvad du kan lære på få minutter.
Trin
Metode 1 af 2: Del 1: Tilføjelse af brøker med samme nævner

1. Tjek nævnerne (tallene under linjen) for hver brøk. Hvis de har det samme tal, så har du at gøre med brøker med ens nævnere. Hvis ikke, spring næste afsnit over.
2. Her er to eksempler på problemer, vi vil arbejde på i dette afsnit. Når du kommer til det sidste trin, bør du forstå, hvordan addition virker.


3. Tag de to tællere (tallene over linjen) og læg dem sammen. Det er lige meget hvor mange brøker du har, hvis de har samme nævner kan du bare lægge alle tællere sammen.


4. Konstruer den nye fraktion. Tag summen af de tællere, du opnåede i trin 2; denne sum bliver den nye tæller. Brug nævneren af brøkerne fra det foregående trin. Dette vil blive den nye nævner; denne nævner forbliver altid den samme, når du tilføjer brøker med den samme nævner


5. Forenkle, hvis du kan. Forenkle den nye brøk for at sikre, at tallene er så små som muligt.

Metode 2 af 2: Anden del: Tilføjelse af brøker med ulige nævnere

1. Tjek nævnerne (tallene under brøklinjen) for hver brøk. Hvis nævnerne er ulige, skal du finde en måde at gøre dem lige. Læs videre for at lære hvordan.
2. Her er to eksempler på problemer, vi vil arbejde med i dette afsnit. Når vi kommer til det sidste trin, ved du, hvordan du tilføjer brøker med ulige nævnere sammen.


3. Find en passende nævner. Du kan gøre dette ved at lede efter det fælles multiplum af nævnerne. En nem måde at finde det på er blot at gange begge nævnere. Hvis en af nævnerne er et multiplum af den anden, skal du bare gange den anden brøk.


4. Gang begge tal i den første brøk med nævneren i den anden brøk. Der er ingen ændring i brøkens værdi; vi ændrer bare, hvordan brøken ser ud. Det er stadig den samme brøkdel.


5. Gang begge tal i den anden brøk med nævneren i den første brøk. Igen ændrer vi ikke værdien af brøken, kun hvordan den ser ud. Det er stadig den samme brøkdel.

6. Placer begge brøker ved siden af hinanden med deres nye tal. De er ikke blevet lagt sammen endnu, bare lidt tålmodighed! Det, vi har gjort, er at gange hver brøk med et passende tal, med det mål at gøre begge nævnere ens.


7. Læg tællere for begge brøker sammen.


8. Tag den lige nævner, du beregnede i trin 2, og brug den som nævneren for den nye brøk. Det er i øvrigt selvfølgelig den samme nævner, som du allerede ser i den ændrede brøk.




9. Forenkle brøken. Forenkle brøken ved at dividere både tæller og nævner med den største fælles divisor.


Tips
Artikler om emnet "Læg brøker sammen"
Оцените, пожалуйста статью
Populær