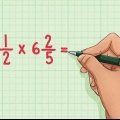Konvertering af uægte brøker til blandede tal: 9 trin (med billeder)

Indhold

Trin
- Metode 1 af 2: Konvertering af en uægte brøk
- Metode 2 af 2: Løsning af prøveproblemer
Tips

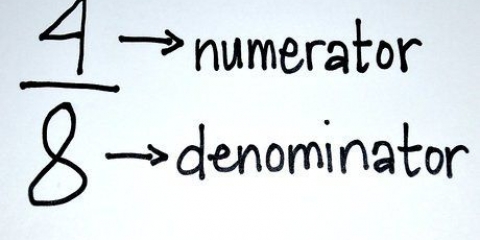
I matematik er uægte brøker dem, hvor tælleren (det øverste tal) er større end eller lig med nævneren (det nederste tal). At konvertere en uægte brøk til et blandet tal (ved at bruge en brøk og et helt tal, såsom 2 3/4), dividere tælleren med nævneren. Skriv hele svaret ved siden af en brøk, med resten i tælleren og den oprindelige nævner nedenfor - du har nu en blandet brøk!

Trin

Metode 1 af 2: Konvertering af en uægte brøk

1. Divider tælleren med nævneren. Begynd at skrive din uægte brøk ned. Derefter divideres tælleren med nævneren - med andre ord regner du divisionssummen ud som vist. Glem ikke at skrive resten ned.

Lad os tage et eksempel. Lad os sige, at vi skal konvertere brøken 7/5 til et blandet tal. Vi dividerer først 7 med 5, såsom:
7/5 → 7 ÷ 5 = 1 R2

Billede med titlen Konverter ukorrekte brøker til blandede tal Trin 2

2. Skriv svarets hele nummer. Hele tallet for dit blandede tal (det store tal til venstre for din brøk) er svaret på hele tallet af divisionssummen. Med andre ord, skriv bare divisionsbesvarelsen uden resten.

I vores eksempel ville vi udelade resten og bare 1 skriv det ned (da vores svar er 1 R2).

Billede med titlen Konverter ukorrekte brøker til blandede tal Trin 3

3. Lav en brøkdel af resten og den oprindelige nævner. Nu skal vi finde brøkdelen af det blandede tal. Indsæt resten af divisionen i tælleren og brug den samme nævner af din oprindelige uægte brøk. Sæt denne brøk ud for dit hele tal, og du har dit blandede tal!

I vores eksempel er resten lig med 2. Hvis vi sætter dette som en tæller over den oprindelige nævner (5), får vi 2/5. Vi sætter dette ved siden af vores svar på hele tallet (1) og får det endelige blandede tal. Som følger:

1 2/5.

Billede med titlen Konverter ukorrekte brøker til blandede tal Trin 4

4. For at gøre dette til en uægte brøk igen, tilføjer vi hele tallet til tælleren. Blandede tal ser godt ud på papiret og er nemme at læse, men er ikke altid det bedste valg. Hvis vi for eksempel multiplicerer en brøk og et blandet tal, vil vores job være meget lettere, hvis vi konverterer det blandede tal tilbage til en uægte brøk. Det gør du ved blot at gange hele tallet med nævneren og lægge til tælleren.

Hvis vi vil lave en uægte brøk fra svaret på vores eksempel (1 2/5), kan vi gøre det sådan her:

1 × 5 = 5 → (2 + 5)/5 = 7/5

Metode 2 af 2: Løsning af prøveproblemer

Billede med titlen Konverter ukorrekte brøker til blandede tal Trin 5

1. Konverter 11/4 til et blandet tal. Dette problem er enkelt - bare løs det nøjagtigt som ovenfor. Se nedenfor for en trin-for-trin løsning.

11/4 — for at starte skal vi dividere tælleren med nævneren.
11 ÷ 4 = 2 R 3 — nu skal vi lave en brøkdel af resten og vores oprindelige nævner.
11/4 = 2 3/4

Billede med titlen Konverter ukorrekte brøker til blandede tal Trin 6

2. Konverter 99/5 til et blandet tal. Vi har at gøre med en meget stor tæller her, men lad det ikke narre dig - metoden er nøjagtig den samme! Se nedenunder:

99/5 - hvor mange gange går 5 til 99? Da 5 går nøjagtigt 20 gange i 100, kan du antage, at 5 går 19 gange i 99.

99 ÷ 5 = 19 R 4 — nu laver vi bare det blandede tal som før.

99/5 = 19 4/5

Billede med titlen Konverter ukorrekte brøker til blandede tal Trin 7

3. Konverter 6/6 til et blandet tal. Hidtil har vi kun beskæftiget os med uægte brøker, hvor tælleren er større end nævneren. Men hvad sker der, når begge er ens? Se nedenfor for at finde ud af det.

6/6 - seks går en gang ud af seks, selvfølgelig uden hvile.

6 6 = 1 R0. Da en brøk med 0 i tælleren altid er lig med nul, behøver vi ikke at sætte en brøk ud for vores hele tal.

6/6 = 1

Billede med titlen Konverter ukorrekte brøker til blandede tal Trin 8

4. Konverter 18/6 til et blandet tal. Hvis tælleren er et multiplum af nævneren, skal du ikke bekymre dig om resten - lav bare divisionssummen for at få dit svar. Se nedenunder.

18/6 — da vi ved, at 18 kun er 6 × 3, ved vi, at vi vil have en rest på 0, så vi behøver ikke bekymre os om brøkdelen af vores blandede tal.

18/6 = 3

Billede med titlen Konverter ukorrekte brøker til blandede tal Trin 9

5. Konverter -10/3 til et blandet tal. Negativer fungerer nøjagtigt det samme som positive tal. Se nedenunder:

-10/3

-10 ÷ 3 = -3 R1

-10/3 = -3 1/3

Tips

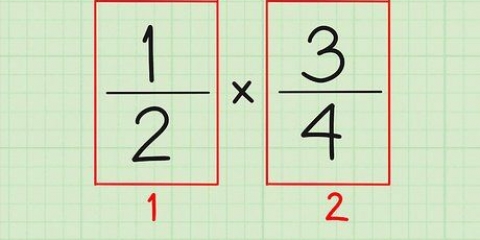
Ukorrekte brøker er ikke nødvendigvis forkert. Faktisk er de nogle gange mere nyttige end blandede tal. For eksempel, hvis du skal gange to brøker, er uægte brøker bedre, fordi du bare skal gange tællere og nævnere sammen for at få dit svar: f.eks. 1/6 × 7/2 = 7/12. Gang nu 1/6 × 3 1/2 — ikke rigtig let.
På den anden side er blandede tal normalt mest nyttige, når man skal beskrive noget i det virkelige liv. For eksempel kræver en opskrift 4 1/2 kopper mel, ikke 9/2 kopper mel.