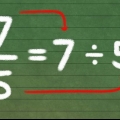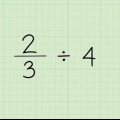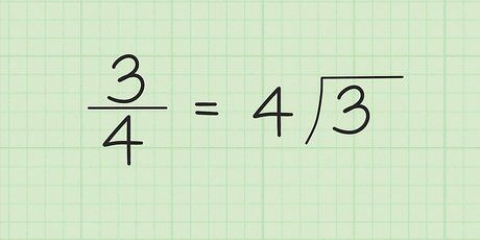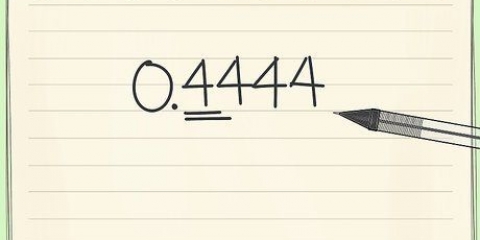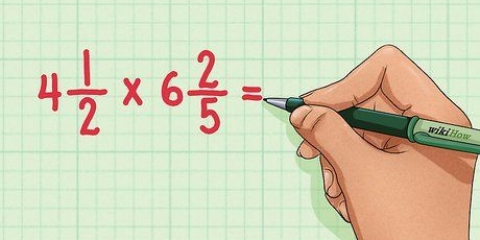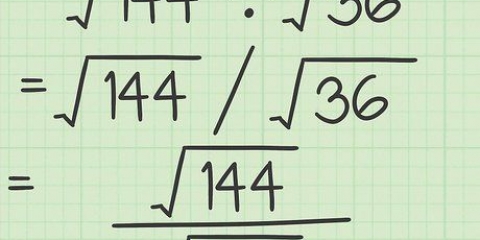For eksempel: i brøken  , 4 er nævneren, hvilket indikerer, at en helhed er opdelt i fire lige store dele eller kvarte.
, 4 er nævneren, hvilket indikerer, at en helhed er opdelt i fire lige store dele eller kvarte. 
For eksempel: i brøken  , 10 er tælleren, hvilket indikerer, at du har 10 stykker, eller 10 af delen som angivet af nævneren.
, 10 er tælleren, hvilket indikerer, at du har 10 stykker, eller 10 af delen som angivet af nævneren. 
For eksempel, hvis din nævner er 4, skal du dele hver cirkel, du tegner, i fire lige store stykker eller kvarte. 
For eksempel: hvis brøken  er, du bliver nødt til at skygge 10 kvartaler.
er, du bliver nødt til at skygge 10 kvartaler. 
For eksempel: i brøken  , så du skygger to hele cirkler, og hele tallet for din blandede fraktion bliver 2.
, så du skygger to hele cirkler, og hele tallet for din blandede fraktion bliver 2. 
i pausen  , Havde du
, Havde du  af en cirkel, så brøkdelen af den blandede fraktion bliver
af en cirkel, så brøkdelen af den blandede fraktion bliver  . Det er også
. Det er også  svarende til
svarende til  .
. 
For eksempel: hvis det blandede nummer  er, kan du forenkle det til
er, kan du forenkle det til  .
. 

Nævneren passer ikke helt ind i tælleren. Resten er så brøkdelen af dit blandede tal. For eksempel: brøken  du beregner som følger
du beregner som følger  . Så hele tallet af din brøk er lig med 2.
. Så hele tallet af din brøk er lig med 2. 
For eksempel:  , så brøken bliver
, så brøken bliver  . Det er også
. Det er også  svarende til
svarende til  .
. 
For eksempel: hvis  er det blandede tal, så kan du forenkle dette til
er det blandede tal, så kan du forenkle dette til  .
.
Forenkling af en uægte brøk
Brøker er tal, der repræsenterer dele af hele tal. Hvis en brøk har en tæller, der er større end nævneren, kaldes den en "forkert brøk" og kan forenkles til et blandet tal (et tal, der kombinerer et heltal og en brøk). Der er ikke noget galt med en uægte brøk, og faktisk er det ofte nemmere at arbejde med i matematik end et blandet tal - men i vores daglige liv bruger vi blandede tal oftere end uægte brøker, så det er nyttigt at vide, hvordan man laver dem.
Trin
Metode 1 af 2: Brug af en model

1. Bestem, om din brøk er falsk. En uægte brøk er en brøk, hvor tælleren er større end nævneren.
- For eksempel:
er en uægte brøk, fordi ti er større end 4.

2. Se nævneren. Nævneren er tallet under brøklinjen. Den fortæller dig, hvor mange lige store dele en helhed er opdelt i.
 , 4 er nævneren, hvilket indikerer, at en helhed er opdelt i fire lige store dele eller kvarte.
, 4 er nævneren, hvilket indikerer, at en helhed er opdelt i fire lige store dele eller kvarte.
3. Se tælleren. Tælleren er tallet over brøklinjen. Den fortæller dig, hvor mange stykker du har.
 , 10 er tælleren, hvilket indikerer, at du har 10 stykker, eller 10 af delen som angivet af nævneren.
, 10 er tælleren, hvilket indikerer, at du har 10 stykker, eller 10 af delen som angivet af nævneren.
4. Tegn cirkler for at repræsentere helheden. Divider hver helhed med nævneren af din brøk.

5. Skygge stykkerne i henhold til din tæller. Tallet i tælleren fortæller dig, hvor mange stykker du skal skygge.
 er, du bliver nødt til at skygge 10 kvartaler.
er, du bliver nødt til at skygge 10 kvartaler.
6. Tæl hvor mange hele cirkler du klækker. For at forenkle en uægte brøk, skal du gøre det til et blandet tal, som inkluderer et helt tal og en brøk sammen. Antallet af hele cirkler, du skygger, repræsenterer hele antallet af din blandede fraktion. Skriv dette nummer ned.
 , så du skygger to hele cirkler, og hele tallet for din blandede fraktion bliver 2.
, så du skygger to hele cirkler, og hele tallet for din blandede fraktion bliver 2.
7. Tæl hvor mange dele af en helhed du har skygget. De resterende skraverede dele vil repræsentere brøkdelen i dit blandede tal. Skriv denne brøk ud for dit hele tal, og du har dit blandede tal.
 , Havde du
, Havde du  af en cirkel, så brøkdelen af den blandede fraktion bliver
af en cirkel, så brøkdelen af den blandede fraktion bliver  . Det er også
. Det er også  svarende til
svarende til  .
.
8. Forenkle dit svar, hvis det er nødvendigt. Nogle gange skal brøkdelen af dit blandede tal forenkles, før du når det endelige svar.
 er, kan du forenkle det til
er, kan du forenkle det til  .
.Metode 2 af 2: Brug af Share

1. Bestem, om din brøk er falsk. En uægte brøk er en brøk, der har en større tæller end dens nævner.
- For eksempel:
er en uægte brøk, fordi 10 er større end 4.

2. Divider tælleren med nævneren. Husk at linjen i en brøk kan tolkes som en divisionsbjælke. For at forenkle en uægte brøk, skal du gøre den til et blandet tal -- et heltal med en brøk. Antallet af gange du kan dividere tælleren ligeligt med nævneren vil være hele tallet for dit blandede tal. Skriv dette tal ned sammen med resten.
 du beregner som følger
du beregner som følger  . Så hele tallet af din brøk er lig med 2.
. Så hele tallet af din brøk er lig med 2.
3. Lav en brøkdel af resten. For at gøre dette skal du tage resten og placere den over nævneren af den oprindelige uægte brøk. Placer denne nye brøk efter hele tallet, og du har dit blandede tal.
 , så brøken bliver
, så brøken bliver  . Det er også
. Det er også  svarende til
svarende til  .
.
4. Forenkle dit svar, hvis det er nødvendigt. Nogle gange skal brøkdelen af dit blandede tal forenkles, før du når dit endelige svar.
 er det blandede tal, så kan du forenkle dette til
er det blandede tal, så kan du forenkle dette til  .
.Tips
- For at konvertere et blandet tal tilbage til en uægte brøk skal du gange hele tallet med nævneren og tilføje produktet til tælleren.
- Gem nævneren. For eksempel:
kan omskrives som
, fordi
.
- Uægte brøker kan også nogle gange repræsentere heltal, som f.eks
.
Artikler om emnet "Forenkling af en uægte brøk"
Оцените, пожалуйста статью
Populær