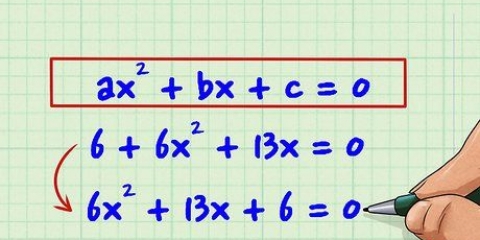For eksempel: hvis du vil dele 20 op i faktorer, kan du skrive det som 4×5. Bemærk, at variable led også kan skrives som faktorer. - For eksempel kan 20x skrives som 4 (5x). Primtal kan ikke skrives som faktorer, fordi de kun er delelige med sig selv og 1. 
huhflagermus mhæve otte Wryk Vformere sig delen Otælle -entrække fra 

Lad os f.eks. finde lignende led i vores ligning 1 + 2x - 3 + 4x. 2x og 4x har begge den samme variabel hævet til samme potens (i dette tilfælde har x-variablerne overhovedet ingen eksponent). Desuden er 1 og -3 lige store led, fordi ingen af dem har en variabel. Så i denne ligning er 2x og 4x og 1 og-3 lige vilkår. 
Vi lægger de lignende udtryk sammen i vores eksempel. 2x + 4x = 6x 1 + -3 = -2 
I vores eksempel var de forenklede udtryk 6x og -2, så det nye udtryk bliver 6x - 2. Dette forenklede udtryk svarer til originalen (1 + 2x - 3 + 4x), men er kortere og lettere at beregne med. Det er lettere at faktorisere, hvilket, som vi vil se nedenfor, er en vigtig færdighed at kunne simplificere. 
Antag for eksempel, at vi har ligningen 5(3x-1) + x((2x)/(2)) + 8 - 3x. Så ville det være forkert umiddelbart at betragte 3x og 2x som lige led og kombinere dem, fordi parenteserne i udtrykket dikterer, at vi skal udføre andre operationer først. Lad os først udføre de aritmetiske operationer i udtrykket i henhold til rækkefølgen af operationerne for at få de termer, vi har godt kan bruge. Se nedenunder: 5(3x-1) + x((2x)/(2)) + 8 - 3x 15x - 5 + x(x) + 8 - 3x 15x - 5 + x + 8 - 3x. passere nu da de eneste operationer tilbage er addition og subtraktion, kan vi kombinere lignende udtryk. x + (15x - 3x) + (8 - 5) x + 12x + 3 

Lad os faktorisere vores ligning ved hjælp af den største fælles divisor, 3. Det gør vi ved at dividere hvert led med 3. 9x/3 = 3x 27x/3 = 9x -3/3 = -1 Så det nye udtryk er 3x + 9x - 1. 
For vores eksempeludtryk, 3x + 9x - 1, sætter vi udtrykket i parentes og multiplicerer dette led med den største fælles divisor af den oprindelige ligning for at konvertere 3 (3x + 9x - 1) at få. Denne ligning svarer til originalen, 9x + 27x - 3. 
Antag, at vores oprindelige eksempeludtryk, 9x + 27x - 3, er lig med tælleren for en større brøk med 3 som nævner. Denne fraktion ser således ud: (9x + 27x - 3)/3. Vi kan bruge faktorisering til at simplificere denne brøk. Tilføj den faktoriserede form af vores oprindelige udtryk til tælleren: (3(3x + 9x - 1))/3 Bemærk, at både tælleren og nævneren har 3 som koefficient. Hvis du dividerer tælleren og nævneren med 3, får du: (3x + 9x - 1)/1. Fordi en brøkdel med "1" i nævneren er lig med led i tælleren, kan vi sige, at vores oprindelige brøk kan simplificeres til 3x + 9x - 1. 

Lad os tage et simpelt eksempel - √(90). Hvis vi tager tallet 90 som et produkt af de to faktorer, 9 og 10, kan vi beregne kvadratroden af 9 for at få 3, og sætte det foran radikalet. Med andre ord: (90) √(9×10) (√(9) × √(10)) 3 × √(10) 3√(10) 
Antag for eksempel, at vi har udtrykket 6x × 8x + (x/x). I alle tilfælde, hvor det er nødvendigt at gange eller dividere eksponenter, trækker eller adderer vi henholdsvis eksponenterne for hurtigt at løse et forenklet udtryk. Se nedenunder: 6x × 8x + (x/x) (6×8)x + (x) 48x + x For en forklaring, se nedenfor: At multiplicere eksponentielle led er i det væsentlige det samme som at gange lange rækker af led uden eksponenter. For eksempel fordi x = x x x x x og x= x x x x x x x x, x x x = (x x x x x) x (x x x x x x x x) eller x. Ligeledes er at dividere eksponentielle led det samme som at dividere lange rækker af led uden eksponenter. x/x = (x × x × x × x × x)/(x × x × x). Da ethvert led i tælleren kan annulleres mod det samme led i nævneren, står vi tilbage med to gange et x i tælleren og ingen i nævneren, hvilket efterlader os med x som svaret.
Forenkling af matematiske ligninger
Indhold
At være i stand til at forenkle algebraiske ligninger er en væsentlig del af at mestre det grundlæggende i algebra og et ekstremt værdifuldt værktøj for alle matematikere at have. Forenkling gør det muligt for en matematiker at ændre et komplekst, langt og/eller klodset udtryk til en enklere eller mere bekvem, men tilsvarende form. Det grundlæggende i at forenkle er ret nemt at lære - selv for nogen, der hader matematik. Ved at følge nogle få enkle trin er det muligt at forenkle mange af de mest almindelige algebraiske udtryk uden nogen særlig matematisk viden.
Trin
Metode 1 af 4: Forståelse af nøglebegreber

1. Bestemme "lige vilkår" i henhold til deres variabler og beføjelser. At besidde i algebra "lige vilkår" over de samme variable, hævet til samme styrke. Med andre ord er to udtryk "lignende", når de har de samme variabler eller slet ingen, og når hver variabel har den samme styrke, eller ingen. Rækkefølgen af variabler inden for et led er ligegyldigt.
- For eksempel er 3x og 4x lige led, fordi hvert led har en variabel x hævet til anden potens. Variablen x og x er ikke lige store led, fordi x har en forskellig potens i hvert led. Ligeledes er -3yx og 5xz ikke lige led, fordi hvert led er opbygget af forskellige variable.

2. Faktor ved at skrive tallene som produktet af to faktorer. Faktorisering er en måde at skrive et givet tal som et produkt af to faktorer. Tal kan være opbygget af flere faktorer – for eksempel tallet 12, som kan dannes af 1 × 12, 2 × 6 og 3 × 4, så vi kan sige, at 1, 2, 3, 4, 6, og 12 er alle faktorer af 12. En anden måde at se det på er, at faktorerne for et tal er de tal, som det er deleligt med.

3. Brug mnemonikken `How Should We Get Rid Of The Inadequacies` (eller som et akronym HMWVDOA) til at huske rækkefølgen af operationerne. Nogle gange er det at forenkle et udtryk bare at udføre operationerne i udtrykket, indtil der ikke kan gøres mere. I så fald er det vigtigt at kende rækkefølgen af operationerne for at undgå beregningsfejl. Denne mnemonic kan hjælpe dig med at huske rækkefølgen af redigeringer - bogstaverne svarer til den type redigeringer du skal udføre og i hvilken rækkefølge. Hvis der er multiplikationer og divisioner i den samme opgave, bliver du nødt til at udføre disse operationer fra venstre mod højre, når du kommer til det punkt. Det samme gælder for addition og subtraktion. Billedet ovenfor giver et svar, der ikke er korrekt. Det sidste trin lykkedes ikke med addition og subtraktion fra venstre mod højre. Først blev det tilføjet. Der skal være 25 - 20 = 5 og derefter 5 + 6 = 11.
Metode 2 af 4: Kombination af lignende udtryk

1. Skriv dine ligninger ned. De enkleste matematiske ligninger (dem med kun få variable og koefficienter som heltal, uden brøker, kvadratrødder osv.) kan ofte løses i få trin. Som med de fleste matematiske problemer er det første skridt til at forenkle en ligning at skrive ligningen!
- For de næste trin tager vi udtrykket 1 + 2x - 3 + 4x som et eksempel.

2. Bestem, hvad de lignende udtryk er. Se nu efter lignende udtryk i din ligning. Husk, at ens udtryk begge har samme variable(r) og eksponent(er).

3. Kombiner lignende udtryk. Nu hvor du har bestemt de lignende udtryk, kan du begynde at kombinere dem for at forenkle din ligning. Læg udtryk sammen (eller træk dem fra i tilfælde af negative udtryk) for at forenkle hvert sæt udtryk (med de samme variabler og eksponenter) til et led.

4. Lav et forenklet udtryk for dine forenklede udtryk. Efter at have kombineret dine lignende udtryk, konstruer et udtryk ud fra dit nye, mindre sæt af termer. Du skulle nu have et enklere udtryk med et led for hvert sæt af variabler og eksponenter i det oprindelige udtryk. Dette nye udtryk svarer til det første.

5. Overhold rækkefølgen af operationer, når du kombinerer lignende udtryk. I meget enkle udtryk som dem, vi behandlede i øvelserne ovenfor, er det let at genkende lignende udtryk. I de mere komplekse udtryk, såsom dem med termer i parentes, brøker og rødder, vil det ikke umiddelbart være tydeligt at kombinere ens udtryk. I disse tilfælde skal du følge rækkefølgen af operationer og udføre operationerne på termerne i dit udtryk, indtil du kun står tilbage med addition og subtraktion.
Metode 3 af 4: Factoring

1. Find den største fælles divisor i udtrykket. Factoring er en måde at forenkle udtryk ved at fjerne faktorer, der optræder i alle udtryk i udtrykket. For at starte skal du finde den største fælles divisor af alle led i udtrykket - med andre ord det største tal, som alle led i udtrykket er delelige med.
- Antag, at vi tager ligningen 9x + 27x - 3. Bemærk, at hvert led i denne ligning er deleligt med 3. Fordi ingen af vilkårene er fuldt deleligt med et andet, større antal, det kan vi sige 3 er den største fællesnævner for vores udtryk.

2. Divider termerne i udtrykket med den største fælles divisor. Divider derefter hvert led i din ligning med den største fælles divisor, du lige har fundet. De resulterende udtryk vil alle have mindre koefficienter end dem i det oprindelige udtryk.

3. Skriv dit udtryk som produktet af den største fælles divisor og de resterende led. Dit nye udtryk er ikke det samme som det gamle, så det er ikke korrekt at sige, at det er den forenklede version. For at gøre det nye udtryk lig med det gamle, bliver vi nødt til at tage højde for, at det er divideret med den største fælles divisor. Sæt dit nye udtryk i parentes og skriv den største fælles divisor af den oprindelige ligning som koefficienten for udtrykket også i parentes.

4. Faktor til at forenkle brøker. Du undrer dig måske nu over, hvorfor faktorisering er nyttig, hvis det nye udtryk skal ganges igen efter at have fjernet den største fælles divisor. Factoring giver en matematiker mulighed for at bruge en række tricks til at forenkle et udtryk. Et af de nemmeste af disse tricks bruger det faktum, at multiplikation af tæller og nævner af en brøk med det samme tal giver en brøk i samme proportioner. Se nedenunder:
Metode 4 af 4: Anvend forenkle

1. Forenkle brøker ved at dividere med lige store faktorer. Som nævnt ovenfor, hvis tælleren og nævneren for et udtryk har de samme faktorer, kan disse faktorer fjernes fra brøken. Nogle gange kræver dette, at tælleren, nævneren eller begge skal faktoriseres (som det var tilfældet i eksemplet ovenfor), mens de delte faktorer i andre tilfælde er umiddelbart synlige. Bemærk at det også er muligt at dividere de enkelte led i tælleren med udtrykket i nævneren, for at få et forenklet udtryk.
- Lad os tage fat på et eksempel, der ikke nødvendigvis kræver, at du skriver dem ud for at forenkle. Antag at du har brøken (5x + 10x + 20)/10, du kan dividere hvert led i tælleren med 10 i nævneren for at forenkle helheden, selvom "5" i 5x ikke større end 10 og det er ikke muligt at vælge 10 som faktor.
- Ved at gøre dette får vi ((5x)/10) + x + 2. Hvis vi vil, kan vi omskrive det første led som (1/2)x for at få (1/2)x + x + 2.

2. Brug kvadratrødder til at forenkle rødder. Udtryk under tegnet af en kvadratrod kaldes kvadratrodsligninger. Du kan forenkle dette ved at bestemme kvadratrødderne (faktorer, der selv danner en anden potens af et heltal), hvorefter du trækker kvadratroden af disse faktorer fra for at fjerne dem fra det radikale tegn.

3. Læg eksponenterne sammen, når du multiplicerer to eksponentielle led, og træk dem fra, når du dividerer. Nogle algebraiske ligninger kræver multiplikation eller division af eksponentielle udtryk. Du regner ikke ud hvert eksponentielt led, og du multiplicerer eller dividerer ikke manuelt, men tælle man lægger eksponenterne for hvert led sammen, når man ganger dem sammen og trækker du dem når du deler dem, sparer du en masse tid. Du kan også anvende dette koncept til at forenkle ligninger med flere variable.
Tips
- Husk, at du skal betragte disse tal som positive eller negative. Mange mennesker bliver hængende med dette og tænker, "Hvilket tegn skal jeg sætte her?"
- Bed om hjælp, hvis du har brug for det!
- At forenkle matematiske ligninger er ikke let, men når du først har fået styr på det, kan du bruge det resten af dit liv.
Advarsler
- Pas på ikke at tilføje nogle ekstra tal, eksponenter eller operationer, der ikke hører hjemme der.
- Vær altid opmærksom på lige vilkår og lad ikke eksponenterne narre dig.
Artikler om emnet "Forenkling af matematiske ligninger"
Оцените, пожалуйста статью
Populær