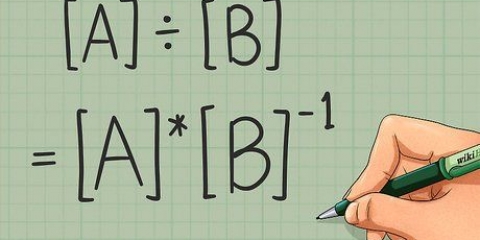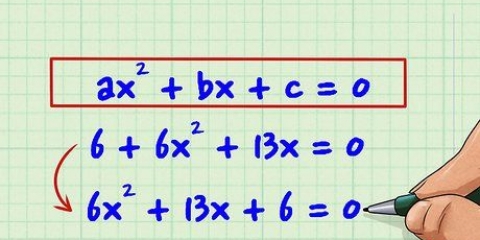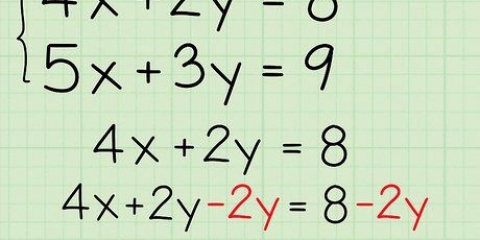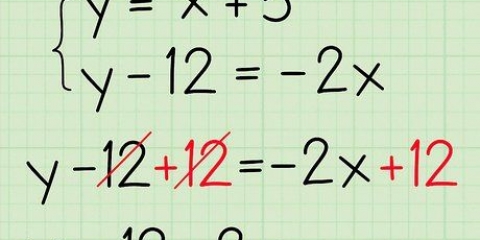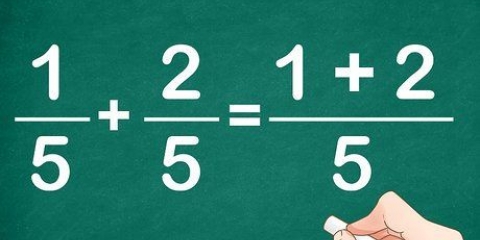→
→ 
 →
→ 
 →
→ 
Bemærk, hvordan minustegnet forbliver foran 2`eren. Når et led trækkes fra, forbliver minustegnet foran det. 
Øvelsesopgave: .
. Faktorer på 3:1, 3 Faktorer på 6: 1, 2, 3, 6. `Den største fælles divisor er 3`. 
Øvelsesopgave: .
. Find de største fælles divisorer: 3 Sådan fjerner du faktor fra begge udtryk:

Øvelsesopgave:
Find de største fælles divisorer: 3 Sådan fjerner du faktor fra begge udtryk:
Multiplicer faktor med nyt udtryk:
Endeligt opløst svar: 

For at omarrangere vilkår:
Find den største fælles divisor:
Sådan fjerner du faktor fra begge udtryk:
Multiplicer faktor med nyt udtryk:
Tjek svar:


Øvelsesopgave:
Lige til nul:


Øvelsesopgave:
Lige til nul:
Opløse:

Øvelsesopgave:
Lige til nul:
Opløse:
Gør begge led lig med nul 0: 




y = 0 

y = 4 


 Dette svar er korrekt
Dette svar er korrekt

 Dette svar er også korrekt.
Dette svar er også korrekt.

Oprindelig opgave:
For at omarrangere vilkår:
Sådan flettes lignende udtryk:
Find de største fælles divisorer:
Opløse:

Formlen for forskellen mellem perfekte kvadrater:
Øvelsesopgave:
Bestem kvadratrødderne: 

Anvend kvadratrødder til formel: 

Formel for forskellen mellem tredje magter:
Øvelsesopgave:
Bestem terningrødderne: ![Factoring binomialer {sqrt[ {3}]{8x^{3}}}=2x](https://wikimedia.org/api/rest_v1/media/math/render/svg/77ed49f7f0ab2dfb9de3438ac123641fb683a0a0)
![Factoring binomialer {sqrt[ {3}]{27}}=3](https://wikimedia.org/api/rest_v1/media/math/render/svg/ca5392df17ff31f62e3cae649d51dd36bde856ce)
Anvend terninger på formlen: 

Formel for summen af perfekte terninger:
Øvelsesopgave:
Bestem terningrødderne: ![Factoring binomialer {sqrt[ {3}]{8x^{3}}}=2x](https://wikimedia.org/api/rest_v1/media/math/render/svg/77ed49f7f0ab2dfb9de3438ac123641fb683a0a0)
![Factoring binomialer {sqrt[ {3}]{27}}=3](https://wikimedia.org/api/rest_v1/media/math/render/svg/ca5392df17ff31f62e3cae649d51dd36bde856ce)
Anvend kuberne på formlen: 
Factoring binomialer
Indhold
I algebra er binomialer toledsudtryk forbundet med et plus- eller minustegn, som f.eks 
Trin
Del 1 af 3: Factoring binomialer

1. Gennemgå det grundlæggende i factoring igen. Factoring er at dele et stort tal i dets simpleste divisorer. Hver af disse dele kaldes en `faktor`. For eksempel er tallet 6 deleligt med fire forskellige tal: 1, 2, 3 og 6. Så 1, 2, 3 og 6 er faktorerne for 6.
- Faktorerne for 32 er 1, 2, 4, 8, 16 og 32
- Både `1` og det tal, du faktoriserer, er altid faktorer. Så faktorerne for et lille tal som 3 er kun 1 og 3.
- Faktorer er kun de tal, der er fuldt delelige, det vil sige `hele` tallene. Du kan dividere 32 med 3,564 eller 21,4952, men det er ikke faktorer, kun decimaltal.

2. Angiv vilkårene for binomialet for at gøre dem nemmere at læse. Et binomial er intet andet end addition eller subtraktion af to led, hvoraf mindst det ene indeholder en variabel. Nogle gange har disse variable eksponenter, som f.eks  eller
eller  . Hvis du forsøger at faktorisere binomialer for første gang, hjælper det at ordne ligningerne i faldende variable termer, hvilket betyder, at den største eksponent kommer sidst. For eksempel:
. Hvis du forsøger at faktorisere binomialer for første gang, hjælper det at ordne ligningerne i faldende variable termer, hvilket betyder, at den største eksponent kommer sidst. For eksempel:
 eller
eller  . Hvis du forsøger at faktorisere binomialer for første gang, hjælper det at ordne ligningerne i faldende variable termer, hvilket betyder, at den største eksponent kommer sidst. For eksempel:
. Hvis du forsøger at faktorisere binomialer for første gang, hjælper det at ordne ligningerne i faldende variable termer, hvilket betyder, at den største eksponent kommer sidst. For eksempel: →
→ 
 →
→ 
 →
→ 

3. Find den største fælles divisor for begge led. Det betyder, at du leder efter det største tal, som begge dele af binomialet er deleligt med. Hvis dette ikke virker, så faktor begge tal på egen hånd og se, hvad det højeste matchende tal er. For eksempel:
 .
.
4. Opdel den største fælles divisor for hvert led. Hvis du kender fællesnævneren, skal du fjerne den fra hvert udtryk. Bemærk, at du bare deler termerne, hvilket gør hver enkelt til et mindre divisionsproblem. Hvis det gøres korrekt, har begge ligninger den samme faktor:
 .
.

5. Multiplicer din faktor med det resulterende udtryk for at runde af. I det sidste problem fjernede du en 3`er, og du får  . Men du ønsker ikke at slippe af med de 3 helt, bare indregn det for at forenkle tingene. Du kan ikke bare slette numre uden at lægge dem tilbage! Gang faktoren med udtrykket for at fuldføre dette afsnit. For eksempel:
. Men du ønsker ikke at slippe af med de 3 helt, bare indregn det for at forenkle tingene. Du kan ikke bare slette numre uden at lægge dem tilbage! Gang faktoren med udtrykket for at fuldføre dette afsnit. For eksempel:
 . Men du ønsker ikke at slippe af med de 3 helt, bare indregn det for at forenkle tingene. Du kan ikke bare slette numre uden at lægge dem tilbage! Gang faktoren med udtrykket for at fuldføre dette afsnit. For eksempel:
. Men du ønsker ikke at slippe af med de 3 helt, bare indregn det for at forenkle tingene. Du kan ikke bare slette numre uden at lægge dem tilbage! Gang faktoren med udtrykket for at fuldføre dette afsnit. For eksempel:




6. Tjek dit arbejde ved at gange til den oprindelige ligning. Hvis du gjorde alt rigtigt, er det nemt at tjekke, om du gjorde det rigtigt. Gang din faktor med begge individuelle udtryk i parentes. Hvis det matcher den oprindelige givne binomiale, så har du gjort det helt rigtigt. Fra start til slut løser vi udtrykket  til praksis:
til praksis:
 til praksis:
til praksis:




Del 2 af 3: Faktorisering af binomialer for at løse ligninger

1. Faktor for at forenkle ligninger, så de er nemmere at løse. Når man løser en ligning med binomialer, især komplekse binomier, kan det virke som om der ikke er nogen måde at få alt til at matche. Prøv for eksempel at løse følgende:  . En måde at gøre dette på, især med eksponenter, er først at faktorisere.
. En måde at gøre dette på, især med eksponenter, er først at faktorisere.
 . En måde at gøre dette på, især med eksponenter, er først at faktorisere.
. En måde at gøre dette på, især med eksponenter, er først at faktorisere. - Øvelsesopgave:
- Husk at binomialer kun kan have to led. Hvis der er mere end to terminer, skal du lære at løse polynomier.

2. Tilføj og træk fra, så den ene side af ligningen er lig med nul. Hele denne strategi er afhængig af en af matematikkens mest fundamentale fakta: noget ganget med nul skal være lig med nul. Så hvis din ligning er lig nul, så skal en af de faktorerede led være lig nul! For at starte skal du addere og trække fra, så den ene side er lig nul.




3. Opløs den ikke-nul side, som du er vant til. På dette tidspunkt lader du bare som om den anden side ikke eksisterer. Find den største fælles divisor, del den, og skab derefter dit faktoriserede udtryk.




4. Sæt vilkårene inden for og uden for parentesen lig med nul. I øveopgaven ganges 2y med (4 – y), og dette skal være lig nul. Da noget ganget med nul er lig med nul, betyder det, at 2y eller (4 – y) skal være lig med nul. Lav to separate ligninger for at finde ud af, hvilken værdi y skal have for at gøre begge sider lig nul.






5. Løs begge ligninger for nul for det eller de endelige svar. Du kan få ét svar eller flere svar. Husk, kun den ene side skal være lig nul, så du kan få et par forskellige værdier for y, der løser den samme ligning. De sidste trin i øvelsesopgaven:





6. Anvend dine svar tilbage til den oprindelige ligning for at sikre dig, at de er korrekte. Når du har fundet de rigtige værdier for y, bør du kunne bruge dem til at løse ligningen. Dette er så simpelt som at prøve hver værdi af y i stedet for variablen som vist nedenfor. Svarene er y = 0 og y = 4, så:


 Dette svar er korrekt
Dette svar er korrekt

 Dette svar er også korrekt.
Dette svar er også korrekt.Del 3 af 3: Håndtering af sværere problemer

1. Husk at variable tæller som faktorer, selv med eksponenter. Husk, at factoring handler om at bestemme, hvilke tal der passer ind i hele tallet. Udtrykket  er en anden måde at sige
er en anden måde at sige  . Det betyder, at du kan placere et hvilket som helst x uden for parentes, hvis det andet led også har en. Behandl variable som almindelige tal. For eksempel:
. Det betyder, at du kan placere et hvilket som helst x uden for parentes, hvis det andet led også har en. Behandl variable som almindelige tal. For eksempel:
 er en anden måde at sige
er en anden måde at sige  . Det betyder, at du kan placere et hvilket som helst x uden for parentes, hvis det andet led også har en. Behandl variable som almindelige tal. For eksempel:
. Det betyder, at du kan placere et hvilket som helst x uden for parentes, hvis det andet led også har en. Behandl variable som almindelige tal. For eksempel: kan faktoriseres, fordi begge udtryk indeholder et t. Det endelige svar bliver
- Du kan endda placere flere variable uden for parentes på samme tid. For eksempel i
begge udtryk indeholder det samme
. Du kan opløse dette i

2. Genkend endnu ikke forenklede binomialer ved at kombinere lignende udtryk. Tag for eksempel udtrykket  . Her ser det ud som om, du har at gøre med fire termer, men hvis du ser nærmere efter, vil du indse, at der kun er to. Du kan tilføje lignende udtryk, og da både 6 og 14 ikke har nogen variabel, og 2x og 3x deler den samme variabel, kan de flettes. Opløsning er så let:
. Her ser det ud som om, du har at gøre med fire termer, men hvis du ser nærmere efter, vil du indse, at der kun er to. Du kan tilføje lignende udtryk, og da både 6 og 14 ikke har nogen variabel, og 2x og 3x deler den samme variabel, kan de flettes. Opløsning er så let:
 . Her ser det ud som om, du har at gøre med fire termer, men hvis du ser nærmere efter, vil du indse, at der kun er to. Du kan tilføje lignende udtryk, og da både 6 og 14 ikke har nogen variabel, og 2x og 3x deler den samme variabel, kan de flettes. Opløsning er så let:
. Her ser det ud som om, du har at gøre med fire termer, men hvis du ser nærmere efter, vil du indse, at der kun er to. Du kan tilføje lignende udtryk, og da både 6 og 14 ikke har nogen variabel, og 2x og 3x deler den samme variabel, kan de flettes. Opløsning er så let:





3. Genkend den særlige "forskel mellem perfekte firkanter". Et perfekt kvadrat er et tal, hvis rod er et heltal, som f.eks 
 ,
, 
 , eller endda
, eller endda 
 Hvis dit binomium er en minussum med to perfekte kvadrater, som f.eks
Hvis dit binomium er en minussum med to perfekte kvadrater, som f.eks  , så kan du bare bruge dem i denne formel:
, så kan du bare bruge dem i denne formel:

 ,
, 
 , eller endda
, eller endda 
 Hvis dit binomium er en minussum med to perfekte kvadrater, som f.eks
Hvis dit binomium er en minussum med to perfekte kvadrater, som f.eks  , så kan du bare bruge dem i denne formel:
, så kan du bare bruge dem i denne formel:





4. Lær at forenkle `forskellen mellem perfekte terninger`. Ligesom de perfekte firkanter er dette en simpel formel, hvor to terninger trækkes fra hinanden. For eksempel,  . Som før, find terningroden af hver og brug den i formlen:
. Som før, find terningroden af hver og brug den i formlen:
 . Som før, find terningroden af hver og brug den i formlen:
. Som før, find terningroden af hver og brug den i formlen:

![Factoring binomialer {sqrt[ {3}]{8x^{3}}}=2x](https://wikimedia.org/api/rest_v1/media/math/render/svg/77ed49f7f0ab2dfb9de3438ac123641fb683a0a0)
![Factoring binomialer {sqrt[ {3}]{27}}=3](https://wikimedia.org/api/rest_v1/media/math/render/svg/ca5392df17ff31f62e3cae649d51dd36bde856ce)


5. Vid, at summen af perfekte terninger også passer ind i en formel. I modsætning til forskellen på perfekte firkanter, kan du bruge tilføjede terninger, som f.eks  , også let at finde med en simpel formel. Dette er næsten nøjagtigt det samme som ovenfor, men med nogle plusser og minusser omvendt. Formlen er lige så nem som de to andre, og alt du skal gøre er at genkende de to terninger i opgaven:
, også let at finde med en simpel formel. Dette er næsten nøjagtigt det samme som ovenfor, men med nogle plusser og minusser omvendt. Formlen er lige så nem som de to andre, og alt du skal gøre er at genkende de to terninger i opgaven:
 , også let at finde med en simpel formel. Dette er næsten nøjagtigt det samme som ovenfor, men med nogle plusser og minusser omvendt. Formlen er lige så nem som de to andre, og alt du skal gøre er at genkende de to terninger i opgaven:
, også let at finde med en simpel formel. Dette er næsten nøjagtigt det samme som ovenfor, men med nogle plusser og minusser omvendt. Formlen er lige så nem som de to andre, og alt du skal gøre er at genkende de to terninger i opgaven:

![Factoring binomialer {sqrt[ {3}]{8x^{3}}}=2x](https://wikimedia.org/api/rest_v1/media/math/render/svg/77ed49f7f0ab2dfb9de3438ac123641fb683a0a0)
![Factoring binomialer {sqrt[ {3}]{27}}=3](https://wikimedia.org/api/rest_v1/media/math/render/svg/ca5392df17ff31f62e3cae649d51dd36bde856ce)

Tips
- Ikke alle binomialer har fælles divisorer! Nogle er allerede blevet forenklet så meget som muligt.
- Hvis du ikke er sikker på, om der er en fælles divisor, skal du først dividere med mindre tal. For eksempel, hvis du ikke umiddelbart kan se, at 16 er fælles divisor for 32 og 16, skal du begynde at dividere begge tal med 2. Dette efterlader 16 og 8, som også kan divideres med 8. Nu har du 2 og 1, de mindste faktorer. Der er tydeligvis en fælles divisor større end 8 og 2.
- Bemærk, at en sjette potens (x) både er et perfekt kvadrat og er en perfekt terning. Så du kan anvende en af de ovennævnte specialformler i en hvilken som helst rækkefølge på et binomium, der er forskellen mellem perfekte sjettepotenser, såsom x - 64. Du kan dog finde det lettere at anvende differensformlen for perfekte kvadrater først, så du kan faktorisere binomialet yderligere.
Advarsler
- Et binomium, der er summen af perfekte kvadrater, kan ikke medregnes.
Artikler om emnet "Factoring binomialer"
Оцените, пожалуйста статью
Populær