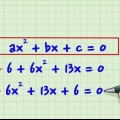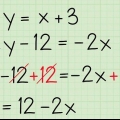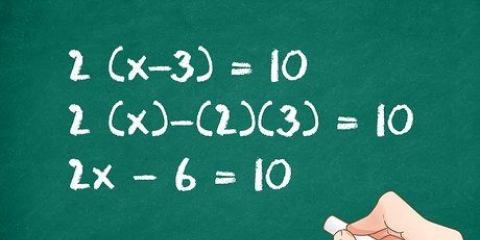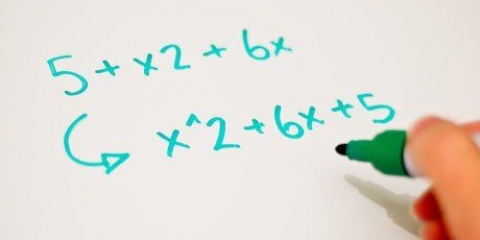For eksempel, 

For eksempel til  i
i  at isolere, du trækker
at isolere, du trækker  ud fra begge sider af ligningen ligningen:
ud fra begge sider af ligningen ligningen:




For eksempel til  skal løses i
skal løses i  , dividere hver side af ligningen med
, dividere hver side af ligningen med  :
:



Så løsningen på er er
er  .
. 

For eksempel omskriv  så hvis
så hvis  .
. 
For eksempel,  .
. 
For eksempel for det kvadratiske polynomium  , du skal finde to tal (
, du skal finde to tal ( og
og  ), rigtigt
), rigtigt  og
og  .
. Fordi du  du ved, at et af tallene vil være negativt.
du ved, at et af tallene vil være negativt. Det burde du se  og
og  . Så du deler dig
. Så du deler dig  på i
på i  og omskriv det kvadratiske polynomium:
og omskriv det kvadratiske polynomium:  .
. 
For eksempel de to første led i polynomiet  er
er  . Et udtryk, der forekommer i begge er
. Et udtryk, der forekommer i begge er  . Dette bliver den opløste gruppe
. Dette bliver den opløste gruppe  .
. 
For eksempel de to andre led i polynomiet  er
er  . Et udtryk, der forekommer i begge er
. Et udtryk, der forekommer i begge er  . Det samme er den opløste gruppe
. Det samme er den opløste gruppe  .
. 
For eksempel, efter faktorisering ved gruppering, bliver  svarende til
svarende til  .
. Det første binomiale er  .
. Det andet binomiale er  .
. Altså det oprindelige kvadratiske polynomium,  kan skrives som det faktoriserede udtryk
kan skrives som det faktoriserede udtryk  .
. 
For eksempel at finde den første løsning af  , sæt det første binomiale udtryk lig med
, sæt det første binomiale udtryk lig med  og miste dig
og miste dig  på. Dermed:
på. Dermed:



Så den første løsning af det kvadratiske polynomium er
er  .
. 
For eksempel at finde den anden løsning til  , sæt det andet binomiale udtryk lig med
, sæt det andet binomiale udtryk lig med  og miste dig
og miste dig  på. Dermed:
på. Dermed:



Så den anden løsning af det kvadratiske polynomium er svarende til
svarende til  .
.
Løs polynomier
Indhold
Et polynomium er et udtryk, der består af addition og subtraktion af led. Et led kan bestå af variable, konstanter og koefficienter. Når man løser polynomier, forsøger man normalt at finde ud af, for hvilke punkter x = 0. Laveste grads polynomier har en eller to løsninger, afhængigt af om de er lineære polynomier eller kvadratiske polynomier. Disse typer polynomier kan let løses ved hjælp af elementær algebra og factoring. For at løse højere grads polynomier kan du læse artikler på wikiHow.
Trin
Metode 1 af 2: Løsning af et lineært polynomium

1. Bestem, om du har at gøre med et lineært polynomium. Et lineært polynomium er et polynomium af første grad. Det betyder, at ingen variabel vil have en eksponent (eller en eksponent større end 1). Da dette er et førstegradspolynomium, har det præcis én løsning.
- For eksempel,
er et lineært polynomium (eller polynomium), fordi variablen
har ingen eksponent (hvilket er det samme som en eksponent for 1).

2. Gør ligningen lig med nul. Dette er et nødvendigt trin for at løse alle polynomier.


3. Flyt variabelleddet til den ene side. Gør dette ved at addere eller trække konstanten fra begge sider af ligningen. En konstant er et led uden en variabel.
 i
i  at isolere, du trækker
at isolere, du trækker  ud fra begge sider af ligningen ligningen:
ud fra begge sider af ligningen ligningen:



4. Løs variablen. Normalt skal du dividere hver side af ligningen med konstanten. Dette giver dig løsningen af polynomiet.
 skal løses i
skal løses i  , dividere hver side af ligningen med
, dividere hver side af ligningen med  :
:


Så løsningen på er
 er
er  .
.Metode 2 af 2: Løsning af et andengradspolynomium

1. Bestem, om du har at gøre med et kvadratisk polynomium. Et andengradspolynomium er en andengradsligning. Det betyder, at ingen variabel har en eksponent større end 2. Da dette er et andengradspolynomium, er der to løsninger.
- For eksempel,
er et kvadratisk polynomium, fordi variablen
-en
har som eksponent.

2. Sørg for, at polynomiet er skrevet i rækkefølge efter grad. Det betyder, at udtrykket med eksponent  vises først efterfulgt af førstegradsleddet, derefter konstanten.
vises først efterfulgt af førstegradsleddet, derefter konstanten.
 vises først efterfulgt af førstegradsleddet, derefter konstanten.
vises først efterfulgt af førstegradsleddet, derefter konstanten. så hvis
så hvis  .
.
3. Gør ligningen lig med nul. Dette er et nødvendigt trin for at løse alle polynomier.
 .
.
4. Omskriv udtrykket som et fireledsudtryk. Det gør du ved at dividere førstegradsleddet (de  semester). Du leder efter to tal, hvis sum er lig med førstegradskoefficienten, og hvis produkt er lig med konstanten.
semester). Du leder efter to tal, hvis sum er lig med førstegradskoefficienten, og hvis produkt er lig med konstanten.
 semester). Du leder efter to tal, hvis sum er lig med førstegradskoefficienten, og hvis produkt er lig med konstanten.
semester). Du leder efter to tal, hvis sum er lig med førstegradskoefficienten, og hvis produkt er lig med konstanten. , du skal finde to tal (
, du skal finde to tal ( og
og  ), rigtigt
), rigtigt  og
og  .
. du ved, at et af tallene vil være negativt.
du ved, at et af tallene vil være negativt. og
og  . Så du deler dig
. Så du deler dig  på i
på i  og omskriv det kvadratiske polynomium:
og omskriv det kvadratiske polynomium:  .
.
5. Faktor ved gruppering. Det gør du ved at faktorisere et led, der matcher de to første betingelser i polynomiet.
 er
er  . Et udtryk, der forekommer i begge er
. Et udtryk, der forekommer i begge er  . Dette bliver den opløste gruppe
. Dette bliver den opløste gruppe  .
.
6. Faktor den anden gruppe. Det gør du ved at faktorisere et led, der forekommer i de to andre led i polynomiet.
 er
er  . Et udtryk, der forekommer i begge er
. Et udtryk, der forekommer i begge er  . Det samme er den opløste gruppe
. Det samme er den opløste gruppe  .
.
7. Omskriv polynomiet som to binomialer. Et binomial er et udtryk med to led. Du har allerede et binomial, udtrykket i parentes for hver gruppe. Dette udtryk skal være det samme for hver gruppe. Det andet binomiale er lavet ved at kombinere de to udtryk, der er faktoriseret fra hver gruppe.
 svarende til
svarende til  .
. .
. .
. kan skrives som det faktoriserede udtryk
kan skrives som det faktoriserede udtryk  .
.
8. Find først løsningen. Det gør du ved at løse  i det første binomiale.
i det første binomiale.
 i det første binomiale.
i det første binomiale. , sæt det første binomiale udtryk lig med
, sæt det første binomiale udtryk lig med  og miste dig
og miste dig  på. Dermed:
på. Dermed:


Så den første løsning af det kvadratiske polynomium
 er
er  .
.
9. Bestem den anden løsning. Det gør du ved  at løse i det andet binomiale.
at løse i det andet binomiale.
 at løse i det andet binomiale.
at løse i det andet binomiale. , sæt det andet binomiale udtryk lig med
, sæt det andet binomiale udtryk lig med  og miste dig
og miste dig  på. Dermed:
på. Dermed:


Så den anden løsning af det kvadratiske polynomium er
 svarende til
svarende til  .
.Tips
- Du skal ikke bekymre dig om variable som t, eller hvis du har en ligning, der svarer til f(x) i stedet for 0. Hvis spørgsmålet ønsker at se rødder, nuller eller faktorer, skal du behandle det som ethvert andet problem.
- Husk rækkefølgen af operationer, mens du arbejder - ryd først parenteserne, lav derefter multiplikation og division og til sidst addition og subtraktion.
Artikler om emnet "Løs polynomier"
Оцените, пожалуйста статью
Populær