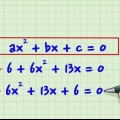Faktoriser

Indhold

Trin
Tips
Advarsler
Fornødenheder

I algebra er en andengradsligning et polynomium bestående af 3 led, af formen ax + bx + c. Polynomier har mange anvendelser inden for matematik og naturvidenskab, og løsning af andengradsligninger er en vigtig færdighed. Mens de fleste andengradsligninger simpelthen kan faktoriseres, er der flere tilfælde, hvor en andengradsligning skal faktoriseres på en særlig måde.Hvis ingen af metoderne i den følgende vejledning er nyttige, kan det være nødvendigt at bruge metoder til faktorisering af højere polynomier.

Trin

Metode 1 af 4: Division 2

1. Ordne argumenterne for andengradsligningen fra største til mindste. Et argument er én variabel i polynomiet; den normale rækkefølge for at placere vilkårene er fra højeste potens til laveste. Så 5 + x + 6x skal bestilles som x + 6x + 5.

Billede med titlen Factor Trinomials Trin 1

2. Udeluk alle faktorer, der forekommer i alle tre led. Hvis konstanterne i andengradsligningen alle er multipla af det samme tal, så kan du sætte dem uden for parentes, eller hvis hver komponent i andengradsligningen har en lige stor variabel, så kan den variabel placeres uden for parentes.

For eksempel, i andengradsligningen -8a + 24a + 144 er hver konstant et multiplum af 8, så 8 kan placeres uden for parentes, hvilket giver -8(a - 3a - 18). Selvom koefficienten -3 og konstanten -18 begge er delelige med -3, er koefficienten 1 for det første led ikke det, så vi kan ikke faktorisere yderligere.

I andengradsligningen - x - 2x - 1 er hvert led deleligt med -1, som efter faktorisering kan skrives som (-1)(x + 2x + 1).

3. Se efter mønstre, der gør det nemmere at løse en andengradsligning. For mere og mere detaljeret information og eksempler, se metoden til løsning af særlige tilfælde af en andengradsligning.

Billede med titlen Factor Trinomials Trin 3

4. Hvis det overhovedet er muligt, så prøv at opdele andengradsligningen i 2 to led på formen (mx + n)(qx + r). Dette er ofte bare at prøve, hvad der virker, men der er tricks, der gør det nemmere. Lad os først antage, at det første led i andengradsligningen (x-leddet) er lig med 1 (leddet ligner mere x end f.eks., 3x). M- og q-værdierne for de to led er 1, så din løsning vil se ud som (x + b)(x + d). Find derefter for din ligning på formen ax + bx + c, værdierne n og r således, at: n * r = c og n + r = b.

I eksemplet er x + 6x + 5, 5 * 1 = 5 og 5 + 1 = 6. Så løsningen er (x + 1)(x + 5).

Hvis ikke alle led i andengradsligningen er positive, så glem ikke at overveje de negative tal. For eksempel, x - 3x - 18 faktor ind i (x - 6)(x + 3), fordi -6 + 3 = -3 og -6 * 3 = -18.

5. Hvis konstanten i det første led ikke er lig med 1 (f.eks. hvis det ligner mere 3x end x), bliver factoring lidt sværere, og via ax + bx + c får du endelig en løsning på formen (mx + n)(qx + r). For en korrekt løsning, m * q = a, m * r + n * q = b, og n * r = c.

Start med at lave en liste over alle mulige faktorer af a og c. Kontroller derefter, hvilket par af faktorer der virker ved at bruge begrænsningerne som angivet ovenfor.

Tag for eksempel 3x + 10x + 8. Mulige faktorpar på 3 er 1 * 3. Mulige faktorpar på 8 er 1 * 8 og 2 * 4. Da 3 * 1 = 3 (leddet i andengradsligningen), 1 * 4 + 2 * 3= 10 (b-leddet) og 2 * 4 = 8 (c-leddet), er løsningen (3x + 4) ( x + 2).

Metode 2 af 4: Factoring Special Cases

Billede med titlen Factor Trinomials Trin 4

1. Tjek om konstanten i det første led eller det tredje led i ligningen er primtal. Et primtal er kun deleligt med sig selv og 1. Dette reducerer antallet af mulige binomiale faktorer. I det foregående eksempel: x + 6x + 5 er der kun 1 muligt sæt binomiale faktorer, (x + 5)(x + 1), fordi 5 er primtal.

Billede med titlen Factor Trinomials Trin 5

2. Tjek om andengradsligningen er et perfekt kvadrat. Dette kræver, at værdierne af koefficienterne a og c for ligningen ax + bx + c er perfekte kvadrater (og positive!), og at værdien af b er det dobbelte af værdien af produktet af kvadratroden af a og c.

(x + a) bliver til x + 2ax + a. For eksempel (x + 3) = x + 6x + 9 og (3x + 2) = 9x + 12x + 4.

Ligeledes bliver (x - a) til x - 2ax + a. For eksempel (x - 3) = x - 6x + 9.

Billede med titlen Factor Trinomials Trin 6

3. For nogle andengradsligninger af formen x - n:

(x + a)(x - a) bliver til x - a. Så x - 9 kan hurtigt indregnes i (x + 3)(x - 3), og 4x - 4 = (2x + 2)(2x - 2).

Metode 3 af 4: Brug af abc-formlen

For andengradsligninger på formen ax + bx + c, der er svære eller umulige at løse, skal du bruge abc-formlen.

1. Lær at bruge abc-formlen.

2. Indtast a, b og c og løs den første del af formlen. Antag, at vi har andengradsligningen x + 5x + 6.

Start med b - 4ac, som er 5 - 4(1)(6) = 1. Kvadratroden af 1 er 1.

Afslut med at løse ligningen. -b + 1 = -5 + 1 = -4. Divider dette med 2a (2 * 1 = 2) for at få -2 som svar.

3. Løs den anden del. Vi ved allerede, at kvadratroden af b - 4ac = 1. -b - 1 = -6. Divider dette med 2a (2) for at få -3.

4. Tjek dine løsninger ved at udfylde dem for x. Nogle gange er et eller flere af svarene ikke gyldige løsninger (f.eks. hvis de er imaginære tal). Men hvis en andengradsligning har en løsning, så finder ligningen den.

Bemærk, at hvis vi havde faktoriseret denne ligning, i stedet for at bruge abc-formlen, ville vi have haft som svar (x + 2)(x + 3). Hvis du sætter denne ligning lig med 0, får du to løsninger, x = 2 og x = -3, som vi også fandt med formlen.

Metode 4 af 4: Det skjulte kvadrat i et polynomium

Nogle andengradsligninger er af højere orden, men i det væsentlige kun andengradsligninger. Når de er blevet anerkendt som sådan, kan du behandle dem som sådan ved at bruge substitution.

1. Se på variablerne i hvert led.For eksempel ser x - 7x + 12 ud til at være en potens af 6, men efter substitution af u=x bliver dette u - 7u + 12. Dette efterlader dig med en ligning, der er meget nemmere at løse.

Mere komplekse substitutioner kan hjælpe med at løse vanskeligere problemer. For eksempel er xy - 7xy + 12y forenklet til xy(u - 7u + 12) og efter substitution u = x/y. En sådan substitution er mulig, når summen af potenserne af de to led er to gange magten af det resterende led.

Billede med titlen Factor Trinomials Trin 7

Billede med titlen Factor Trinomials Trin 8

2. Hvis en sådan substitution kan finde sted, så udregn det simple polynomium, i dette tilfælde, u - 7u + 12 = (u-3)(u-4)

Billede med titlen Factor Trinomials Trin 9

3. Fortryd substitutionen og anvend x på løsningen. Så erstat u med x , x - 7x + 12 = (x - 3)(x - 4). Hvis det er muligt eller ønskes, kan hver faktor forenkles endnu mere.

Tips

Brug Eisensteins kriterium til hurtigt at bestemme, om et polynomium er ikke-reducerbart og ikke-faktorerbart. Dette kriterium gælder for ethvert polynomium, men især for en andengradsligning. Hvis der er et primtal p, som gør de sidste to led delelige og opfylder følgende betingelser, kan polynomiet ikke reduceres:

Konstantleddet (c`et i en andengradsligning af formen ax + bx + c) er en flertal af p, men ikke af p.
Det første led (her, a) er ikke et flertal af p.
For eksempel er 14x + 45x + 51 irreducerbar, fordi den har et primtal (3), der gør både 45 og 51 delelige, men ikke 14 og 51, som ikke er delelige med 3.

Du kan faktorisere polynomier af flere variabler ved hjælp af ovenstående metoder, hvis de er andengradsligninger, der antager en eller anden variabel. Tag for eksempel 4xy - 5x + 15y. Dette kan omskrives som (4x)y + 15y - 5x. Bemærk, at dette passer til formen ax + bx + c, hvor a = 4x og c = 5x. Denne ligning kan så løses med abc-formlen.

Du kan øve dig i faktorisering af andengradsligninger ved at lave opgaver i en bog, der omhandler algebra.

Advarsler

Selvom det er sandt for kvadrater, er andengradsligninger, der kan faktoriseres, ikke nødvendigvis produktet af to binære tal. Et modeksempel er x + 105x + 46 = (x + 5x + 2)(x - 5x + 23).