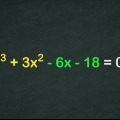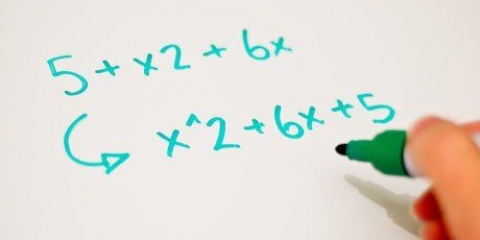Factoring Quadrilateral Equations

Indhold

Trin
Tips
Advarsler
Fornødenheder

Et polynomium indeholder en variabel (x) hævet til en bestemt potens og flere led og/eller konstanter. For at faktorisere et polynomium skal du opdele udtrykket i mindre udtryk, der ganges sammen. Dette kræver et vist niveau af matematik, og det kan derfor være svært at forstå, hvis du ikke er så langt endnu.

Trin

Metode 1 af 7: Kom godt i gang

1. Ligningen. Standardformatet for en andengradsligning er:

ax + bx + c = 0
Start med at sortere termerne i din ligning fra højeste til laveste potens. Tag for eksempel:

6 + 6x + 13x = 0
Vi vil omarrangere dette udtryk for at gøre det nemmere at arbejde med – blot ved at flytte termerne rundt:

6x + 13x + 6 = 0

Billede med titlen Faktor Second Degree Polynomials (Quadratic Equations) Trin 2

2. Find faktorerne ved hjælp af en af metoderne nedenfor. Faktorering af polynomiet vil resultere i to mindre udtryk, der kan ganges sammen for at få det oprindelige polynomium:

6x + 13x + 6 = (2x + 3)(3x + 2)
I dette eksempel er (2x +3) og (3x + 2) faktorer fra det originale udtryk, 6x + 13x + 6.

Billede med titlen Faktor Second Degree Polynomials (Quadratic Equations) Trin 3

3. Tjek dit arbejde! Multiplicer de faktorer, du fandt. Kombiner de lignende udtryk, og du er færdig. Start med:

(2x + 3)(3x + 2)
Lad os teste dette ved at gange termerne med EBBL (første - ydre - indre - sidst), hvilket giver os:

6x + 4x + 9x + 6
Nu lægger vi 4x og 9x sammen, fordi disse er lige store vilkår. Vi ved, at faktorerne er korrekte, fordi vi får den ligning tilbage, vi startede med:

6x + 13x + 6

Metode 2 af 7: Prøv og fejl

Hvis du har et ret simpelt polynomium, kan du måske med det samme se, hvad faktorerne er. For eksempel, efter lidt øvelse, er mange matematikere i stand til at se, at udtrykket 4x + 4x + 1 har faktorerne (2x + 1) og (2x + 1), bare fordi de har set dette så mange gange. (Dette vil naturligvis ikke være så let med mere komplicerede polynomier.) Lad os tage et mindre standardudtryk for dette eksempel:

3x + 2x - 8

Billede med titlen Faktor Second Degree Polynomials (Quadratic Equations) Trin 4

1. Skriv faktorerne ned -en sigt og c semester. Brug formatet ax + bx + c = 0, genkende -en og c vilkår og noter hvilke faktorer der er. For 3x + 2x - 8 betyder dette:

a = 3 og har 1 par faktorer: 1 * 3
c = -8 og den har 4 par af faktorer: -2 * 4, -4 * 2, -8 * 1 og -1 * 8.

Billede med titlen Faktor anden grads polynomier (kvadratiske ligninger) Trin 5

2. Skriv to par parenteser med et tomt mellemrum. Her indtaster du konstanterne for hvert udtryk:

( x )( x )

Billede med titlen Faktor Second Degree Polynomials (Quadratic Equations) Trin 6

3. Udfyld pladsen foran x`erne med nogle mulige faktorer af -en hvor er. For -en udtryk i vores eksempel, 3x, er der kun 1 mulighed:

(3x)(1x)

Billede med titlen Faktor Second Degree Polynomials (Quadratic Equations) Trin 7

4. Udfyld de 2 felter efter x`erne med et par faktorer for konstanterne. Antag, at vi vælger 8 og 1. Indtast dette:

(3x 8)(X 1)

Billede med titlen Faktor Second Degree Polynomials (Quadratic Equations) Trin 8

5. Bestem hvilke tegn (plus eller minus) der skal placeres mellem x-variablerne og tallene. Afhængig af det oprindelige udtryks fortegn er det muligt at finde ud af, hvad konstanternes fortegn skal være. Lad os tage de to konstanter af de to faktorer h og k at nævne:

Hvis ax + bx + c så (x + h)(x + k)
Hvis ax - bx - c eller axe + bx - c så (x - h)(x + k)
Hvis ax - bx + c så (x - h)(x - k)
I vores eksempel, 3x + 2x - 8, er tegnet:(x - h)(x + k), hvilket giver os følgende to faktorer:

(3x + 8) og (x - 1)

Billede med titlen Faktor Second Degree Polynomials (Quadratic Equations) Trin 9

6. Test dit valg med den første-ydre-indre-sidste multiplikation. En hurtig første test for at se, om mellemleddet er mindst den rigtige værdi. Hvis ikke, så har du sandsynligvis den forkerte c valgte faktorer. Lad os teste svaret:

(3x + 8)(x - 1)
Ved multiplikation får vi:

3x - 3x + 8x - 8
Forenkle dette udtryk ved at tilføje de lignende udtryk (-3x) og (8x), og vi får:

3x - 3x + 8x - 8 = 3x + 5x - 8
Vi ved nu, at vi tog de forkerte faktorer:

3x + 5x - 8 3x + 2x - 8

Billede med titlen Faktor Second Degree Polynomials (Quadratic Equations) Trin 10

7. Skift dine valg om nødvendigt. I vores eksempel, lad os prøve 2 og 4 i stedet for 1 og 8:

(3x + 2)(x - 4)
Nu vores c led lig med -8, men det ydre/indre produkt af (3x * -4) og (2 * x) er -12x og 2x, hvilket ikke er det korrekte b term eller +2x får.

-12x + 2x = 10x
10x 2x

Billede med titlen Faktor Second Degree Polynomials (Quadratic Equations) Trin 11

8. Vend om nødvendigt rækkefølgen. Lad os prøve at vende 2 og 4:

(3x + 4)(x - 2)
Nu vores c term (4 * 2 = 8) og stadig OK, men de ydre/indre produkter er -6x og 4x.Ved at kombinere disse får vi:

-6x + 4x = 2x
2x -2x Vi kommer ret tæt på de 2x, hvor vi gerne vil være, men skiltet er ikke rigtigt endnu.

Billede med titlen Faktor Second Degree Polynomials (Quadratic Equations) Trin 12

9. Dobbelttjek om nødvendigt dine karakterer. Vi beholder denne rækkefølge, men ombytter den med minustegnet:

(3x - 4)(x + 2)
Nu c sigt stadig ok, og de ydre/indvendige produkter er nu (6x) og (-4x). Fordi:

6x - 4x = 2x
2x = 2x Vi ser nu den positive 2x tilbage fra det oprindelige problem. Det skal være de rigtige faktorer.

Metode 3 af 7: Dekomponering

Denne metode giver alle mulige faktorer af -en og c vilkår og bruge dem til at finde ud af, hvilke faktorer der er de rigtige. Hvis tallene er meget store, eller gætværket af andre metoder kommer til at tage for lang tid, så brug denne måde. Et eksempel:

6x + 13x + 6

Billede med titlen Factor Second Degree Polynomials (Quadratic Equations) Trin 13

1. Multiplicer -en sigt med c semester. I dette eksempel,, -en er 6 og c er også 6.

6 * 6 = 36

Billede med titlen Faktor Second Degree Polynomials (Quadratic Equations) Trin 14

2. Find b sigt ved factoring og test. Vi leder efter 2 tal, der er faktorer af -en * c , og sammen b sigt (13) form.

4 * 9 = 36
4 + 9 = 13

Billede med titlen Faktor Second Degree Polynomials (Quadratic Equations) Trin 15

3. Erstat de to tal, du får i din ligning, som summen af b semester. Lad os k og h for at repræsentere de 2 tal, vi har, 4 og 9:

ax + kx + hx + c
6x + 4x + 9x + 6

Billede med titlen Faktor Second Degree Polynomials (Quadratic Equations) Trin 16

4. Faktorer polynomiet ved at gruppere. Organiser ligningen, så du kan isolere den største fælles divisor af de to første led og de sidste to led. Begge faktorer bør være de samme. Tilføj GCD`erne sammen og placer dem i parentes ved siden af faktorerne; som et resultat får du de to faktorer:

6x + 4x + 9x + 6
2x(3x + 2) + 3(3x + 2)
(2x + 3)(3x + 2)

Metode 4 af 7: Triple Play

Svarende til nedbrydningsmetoden. `Triple play`-metoden undersøger de mulige faktorer af produktet af -en og c og bruge det til at finde ud af hvad b må være. Tag ligningen som eksempel:

8x + 10x + 2

Billede med titlen Faktor Second Degree Polynomials (Quadratic Equations) Trin 17

1. Multiplicer -en sigt med c semester. Som med nedbrydningsmetoden bruger vi denne til at bestemme kandidaterne til b semester. I dette eksempel: -en er 8 og c er 2.

8 * 2 = 16

Billede med titlen Faktor Second Degree Polynomials (Quadratic Equations) Trin 18

2. Find de 2 tal med dette tal som produkt og med en sum lig med b semester. Dette trin svarer til nedbrydningsmetoden - vi tester kandidater for konstanterne. Produktet af -en og c vilkår er 16, og den c sigt er 10:

2 * 8 = 16
8 + 2 = 10

Billede med titlen Faktor Second Degree Polynomials (Quadratic Equations) Trin 19

3. Tag disse 2 tal og erstat dem i `triple play`-formlen. Tag de 2 tal fra det forrige trin - lad os sætte dem h og k kald dem - og sæt dem i udtrykket:

((ax + h)(ax + k))/ a

Med dette får vi:

((8x + 8)(8x + 2)) / 8

Billede med titlen Faktor Second Degree Polynomials (Quadratic Equations) Trin 20

4. Se hvilken af de to led i nævneren der kan divideres helt med -en. I dette eksempel ser vi på, om (8x + 8) eller (8x + 2) kan divideres med 8. (8x + 8) er deleligt med 8, så vi dividerer dette led med -en og lad os lade den anden være.

(8x + 8) = 8(x + 1)
Udtrykket, vi har beholdt her, er det, der er tilbage efter at have divideret med -en term:(x + 1)

Billede med titlen Faktor Second Degree Polynomials (Quadratic Equations) Trin 21

5. Tag den største fælles divisor (gcd) af den ene eller begge led, hvis det er muligt. I dette eksempel ser vi, at det andet led har en gcd på 2, fordi 8x + 2 = 2(4x + 1). Kombiner dette svar med det udtryk, du opdagede i det foregående trin. Disse er faktorerne i din ligning.

2(x + 1)(4x + 1)

Metode 5 af 7: Forskellen mellem to kvadrater

Nogle koefficienter i et polynomium kan genkendes som "kvadrater" eller også som produktet af 2 af de samme tal. Ved at finde ud af, hvad disse kvadrater er, kan du muligvis faktorisere polynomierne meget hurtigere. Vi tager ligningen:

27x - 12 = 0

Billede med titlen Faktor Second Degree Polynomials (Quadratic Equations) Trin 22

1. Fjern gcd`en fra ligningen, hvis det er muligt. I dette tilfælde ser vi, at 27 og 12 begge er delelige med 3, så vi kan sætte dem separat:

27x - 12 = 3(9x - 4)

Billede med titlen Faktor Second Degree Polynomials (Quadratic Equations) Trin 23

2. Bestem om koefficienterne for din ligning er kvadrater. For at bruge denne metode er det nødvendigt at kunne bestemme roden af begreberne. (Bemærk at vi har udeladt decimaler - fordi disse tal er kvadrater, kan de være produktet af 2 negative tal)

9x = 3x * 3x og 4 = 2 * 2

Billede med titlen Faktor Second Degree Polynomials (Quadratic Equations) Trin 24

3. Ved at bruge den kvadratrod, du har bestemt, kan du nu skrive faktorerne ud. Vi tager -en og c værdier fra det forrige trin: -en = 9 og c = 4, så rødderne til dette er: - √-en = 3 ogc = 2. Disse er koefficienterne for de faktorerede udtryk:

27x - 12 = 3(9x - 4) = 3(3x + 2)(3x - 2)

Metode 6 af 7: ABC-formlen

Hvis intet ser ud til at virke, og du ikke kan faktorisere ligningen, skal du bruge abc-formlen. Tag følgende eksempel:

x + 4x + 1 = 0

Billede med titlen Faktor Second Degree Polynomials (Quadratic Equations) Trin 25

1. Udfyld de tilsvarende værdier i abc-formlen:

x = -b ± √(b - 4ac)
---------------------
2a
Vi får nu udtrykket:

x = -4 ± √(4 - 4•1•1) / 2

Billede med titlen Faktor anden grads polynomier (kvadratiske ligninger) Trin 26

2. Løs for x. Du skulle nu få 2 værdier for x. Disse er:

x = -2 + √(3) eller x = -2 - √(3)

Billede med titlen Faktor Second Degree Polynomials (Quadratic Equations) Trin 27

3. Brug værdierne af x til at bestemme faktorerne. Udfyld x-værdierne opnået i de to ligninger som konstanter. Det er dine faktorer. Hvis vi svarer på de to h og k så skriver vi de to faktorer som følger:

(x - h)(x - k)
I dette tilfælde er det endelige svar:

(x - (-2 + √(3))(x - (-2 - √(3)) = (x + 2 - √(3))(x + 2 + √(3))

Metode 7 af 7: Brug en lommeregner

Hvis det er tilladt (eller påkrævet) at bruge en grafregner, gør dette faktorisering meget lettere, især under eksamener og eksamener. Følgende instruktioner er til en TI-grafregner. Vi bruger ligningen fra eksemplet:

y = x − x − 2

Billede med titlen Faktor Second Degree Polynomials (Quadratic Equations) Trin 28

1. Indtast ligningen i din lommeregner. Du skal bruge ligningsløseren, også kendt som [Y = ]-skærmen.

Billede med titlen Faktor Second Degree Polynomials (Quadratic Equations) Trin 29

2. Tegn en graf af ligningen med lommeregneren. Når du har indtastet ligningen, skal du trykke på [GRAPH] - du skulle nu se en buet linje, en parabel som en grafisk repræsentation af din ligning (og det er en parabel, fordi vi har at gøre med et polynomium).

Billede med titlen Faktor Second Degree Polynomials (Quadratic Equations) Trin 30

3. Find, hvor parablen skærer x-aksen. Da en andengradsligning traditionelt er noteret som ax + bx + c = 0, er disse to x-værdier, der gør ligningen lig med nul:

(-1, 0), (2, 0)
x = -1, x = 2

Hvis du ikke kan se, hvor parablen skærer x-aksen, skal du trykke på [2nd] og derefter [TRACE]. Tryk på [2], eller vælg "nul". Flyt markøren til venstre for et vejkryds, og tryk på [ENTER]. Flyt markøren til højre side af et vejkryds, og tryk på [ENTER]. Flyt markøren så tæt som muligt på krydset og tryk på [ENTER]. Lommeregneren viser x-værdien.Gør det samme for det andet skæringspunkt.

Billede med titlen Faktor Second Degree Polynomials (Quadratic Equations) Trin 31

4. Indtast de x-værdier, du har opnået, i de to faktoriserede udtryk. Hvis vi tager de to x-værdier h og k skriv det ned som et udtryk, så ser det udtryk vi bruger sådan ud:

(x - h)(x - k) = 0
Så vores to faktorer bliver så:

(x - (-1))(x - 2) = (x + 1)(x - 2)

Tips

Hvis du har faktoriseret polynomiet med abc-formlen, og dit svar indeholder rødder, kan du konvertere x-værdierne til brøker for at kontrollere dem.
Hvis et led ikke har nogen koefficient foran sig, så er koefficienten lig med 1, f.eks. x = 1x.
Hvis du har en TI-84 lommeregner, er der et program kaldet SOLVER, der kan løse en andengradsligning for dig. Dette løser også højere grads polynomier.
Efter meget øvelse vil du til sidst lykkes med at løse polynomier udenad. Men bare for at være sikker, er det bedre altid at skrive dem ud.
Hvis et led ikke eksisterer, så er koefficienten lig nul. Så kan det være nyttigt at omskrive ligningen. For eksempel. x + 6 = x + 0x + 6.

Advarsler

Når du lærer dette koncept i matematiktimerne, skal du være opmærksom på, hvad læreren forklarer og ikke bare bruge din egen yndlingsmetode. Du kan blive bedt om at bruge en bestemt metode på en test, eller grafregnere er muligvis ikke tilladt.