Radianmålingerne af enhedscirklen antager altid, at du starter fra punktet (0, 1). For at gøre det klart, hvilket punkt vi henviser til, beskriver vi cirklen som en kompasrose: 

`Øst` er udgangspunktet, så det har du 0 havde radianer. `Nord` = en fjerdedel af cirklens omkreds = /4 = /2 radianer. `Vest` = halvvejs gennem cirklen = /2 = π radianer. `Syd` = tre fjerdedele af cirklen = 2π * ¾ = /2 radianer. Går du langs hele omkredsen, vender du tilbage til udgangspunktet. Du kan angive dette som 2π eller 0. 
/4 /4 /4 /4 (π/2, π, 3π/2 og 2π er allerede blevet angivet.) 
/3 /3 /3 /3 (π og 2π er allerede angivet) 
/6 /6 /6 /6 

Koordinaterne for `Øst` er (1, 0). Koordinaterne for `Nord` er (0, 1). Koordinaterne for `Vest` er (-1, 0). Koordinaterne for `Syd` er (0, -1). Dette fungerer ligesom en normal graf. Du bør selv kunne finde disse koordinater uden at skulle huske dem. 
På /6, er koordinaterne ( ).
). På /4, er koordinaterne ( ).
). På /3, er koordinaterne ( ).
). Bemærk, at der kun er tre tællere. Bevæger du dig i en positiv retning (venstre mod højre for x-værdier, fra bund til top for y-værdier), så er rækkefølgen som følger: 1 → √2 → √3. 
For eksempel kan du tegne en vandret linje mellem /3 og /3. Da koordinaterne ved det første punkt ( ), koordinaterne for det andet punkt (?
), koordinaterne for det andet punkt (? ), hvorved `?` repræsenterer et plus- eller minustegn (+ eller -).
), hvorved `?` repræsenterer et plus- eller minustegn (+ eller -). Her er en hurtigere måde: Tjek radianernes nævner. Alle punkter, der ender på /3, har de samme absolutte koordinater, ligesom alle punkter, der ender på /4 og alle punkter, der ender på /6. 
Tænk grundlæggende regler for diagrammer. Over x-aksen er punkterne positive, under den negative. Til venstre for y er negativ, rigtig er positiv. Start fra kvadrant 1 og tegn linjer til andre punkter. Hvis linjen de y-aksen krydser y-værdien vil skifte fortegn. Hvis linjen de x-aksen krydser, så skifter x-værdien fortegn. Lær `All Students Test Calculus` (ASTC) mod uret. Kvadrant 1 har -enkun positive værdier, kvadrant 2 har kun positive værdier sinus-værdier, har kvadrant 3 kun positive tangens værdier, og kvadrant 4 har kun positive Cosine værdier. Uanset hvilken metode du vælger, er fortegnene (+, +) for kvadrant 1, (-, +) for kvadrant 2, (-, -) for kvadrant 3 og (+,-) for kvadrant 4. 
Kvadrant 1: ( ); (
); ( ); (
); ( ).
). Kvadrant 2: ( ); (
); ( ); (
); ( )
) Kvadrant 3: ( ); (
); ( ); (
); ( )
) Kvadrant 4: ( ); (
); ( ); (
); ( )
)
Husk enhedscirklen
At lære enhedscirklen hjælper dig ikke kun med trigonometri og geometri, men også med differential- og integralregning. Det kan virke som en masse memorering, men når du først forstår, hvordan det fungerer, kan du starte med et par tal fra enhedscirklen og hurtigt finde ud af resten.
Trin
Del 1 af 2: Husk radianerne

1. Tegn to vinkelrette linjer. Placer et kompas på et stort ark papir. Tegn en lodret og en vandret linje. Disse skal skære hinanden nær midten af siden. Disse er x-aksen og y-aksen af grafen.

2. Tegn en cirkel. Brug et kompas til at tegne en stor cirkel centreret i skæringspunktet mellem de to linjer.

3. Forstå radianer. En radian er et vinkelmål. Det er hovedsageligt defineret på en sådan måde, at en person, der går rundt i en cirkel med en Ray af 1 enhed bevæger sig gennem en vinkel på en radian efter at have gået 1 enhed rundt om omkredsen. I næste trin vil vi angive de fire koordinatpunkter med radianværdien. Hvis du husker formlen for forholdet mellem en cirkels omkreds og dens radius, kan du hurtigt regne den ud, men selvom du ikke husker den.

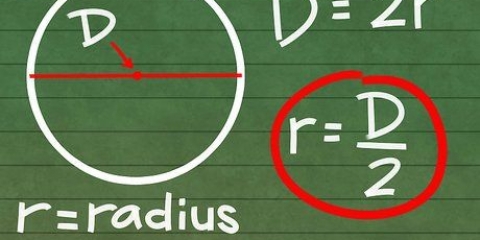
4. Husk at cirklens omkreds er 2π. Omkredsen af en cirkel er lig med 2πr, hvorved r står for radius (radius). Da enhedscirklen har en radius på 1, kan vi forenkle omkredsen til 2π. Radianværdien af ethvert punkt på omkredsen kan findes ved blot at dividere 2π med den del af cirklen, du havde. Dette er meget nemmere end at huske hver enkelt værdi på cirklen.

5. Angiv de fire punkter på x- og y-akserne. Alt du skal gøre er at dele 2π i kvarte:

6. Del cirklen i otte stykker. Tegn nu en diagonal linje gennem hver kvadrant, perfekt gennem midten. Igen, brug division til at finde værdien i radianer:

7. Opdel cirklen i seks segmenter. Tegn nu yderligere linjer, der deler cirklen i seks segmenter. (Du kan bruge en vinkelmåler til dette, startende ved den positive x-akse, hvor hvert segment måler 60 grader). Du kan bruge samme fremgangsmåde som ovenfor for at sikre, at en sjettedel af en cirkel er lig med /6 = /3 radianer. Brug denne etiket til følgende punkter på omkredsen (én i hver kvadrant):

8. Tegn tolvtedele i den. De sidste punkter markeret på de fleste enhedscirkler angiver trin på en tolvtedel af omkredsen. Kun fire af disse er endnu ikke erklæret:
Del 2 af 2: Husk x- og y-koordinaterne (cosinus, sinus)

1. Forstå cosinus og sinus. Enhedscirklen er især nyttig til trigonometriske beregninger med rette vinkler. Hver x-koordinat af et punkt på cirklen er lig med cos(θ) og hver y-koordinat er lig med sin(θ), hvor θ er værdien af vinklen.
- Hvis du har svært ved at huske, så tænk på (cos, sin) `fordi sinus kommer sidst`.
- Du kan udlede dette ved at bruge rette trekanter og definitionen af disse funktioner - husk `soscastoa`?

2. Skriv koordinaterne ned i fire punkter i cirklen. En `enhedscirkel` er simpelthen en cirkel med en radius på præcis én enhed. Brug disse til at finde x- og y-koordinaterne for de fire punkter på cirklen, hvor den skærer en akse. (Vi kalder disse `Øst`, `Nord` osv. for at lette læsningen, men disse er ikke officielle navne).

3. Husk koordinaterne for den første kvadrant. Den første kvadrant er den øverste højre fjerdedel af cirklen, hvor både x-værdier som y-værdier er positive. Dette er de eneste koordinater, du skal huske:
 ).
). ).
). ).
).
4. Tegn lige linjer for at udfylde de andre koordinater. Hvis du kan tegne en perfekt lodret eller en perfekt vandret linje mellem to punkter, så har de samme absolutte værdi som x- og y-koordinater. Med andre ord kan du tegne en linje fra et punkt i de første kvadranter, skrive de samme koordinater ned, hvor du lander, og lade plads til højre for det til tegnet (+ eller -).
 ), koordinaterne for det andet punkt (?
), koordinaterne for det andet punkt (? ), hvorved `?` repræsenterer et plus- eller minustegn (+ eller -).
), hvorved `?` repræsenterer et plus- eller minustegn (+ eller -).
5. Brug symmetri til at finde ud af, om tegnet er positivt eller negativt. Der er flere måder at huske, hvor minustegnene skal placeres på enhedscirklen:

6. Tjek dit arbejde. Her er den fulde liste over koordinatværdier for hvert mærket punkt på cirklen (ikke medregnet de fire punkter på akserne), med uret. Husk, du bør være i stand til at finde alle disse værdier blot ved at huske punkterne i kvadrant 1:
 ); (
); ( ); (
); ( ).
). ); (
); ( ); (
); ( )
) ); (
); ( ); (
); ( )
) ); (
); ( ); (
); ( )
)Tips
- Hvis du har en test eller repetition på enhedscirklen, skal du først tegne cirklen på klippepapir, så du kan bruge den som reference for hver opgave.
- Processen vil være betydeligt hurtigere, hvis du øver dig meget. I fremtiden behøver du måske kun at se x- og y-akserne for at huske alt, eller du behøver måske ikke engang et diagram længere.
Artikler om emnet "Husk enhedscirklen"
Оцените, пожалуйста статью
Populær