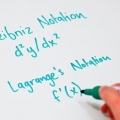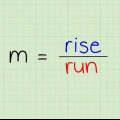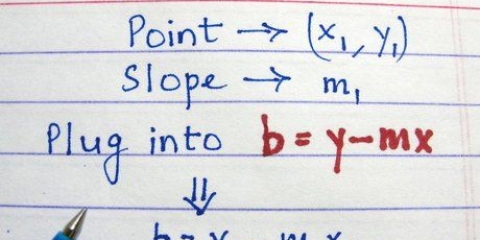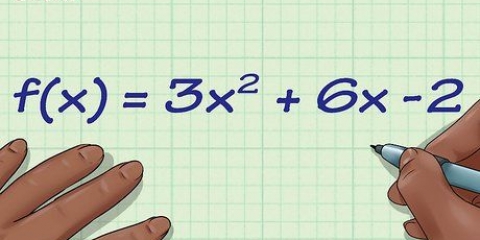Hældning = 2 
Hældning = -1 
hældning = 

Find hældningen af 
Konverter det til formularen  :
: 



Bestem hældningen: Hældning = M = 4 

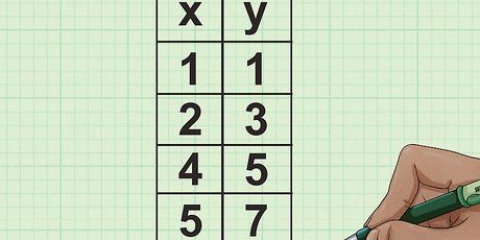
I hvert par er x-koordinaten det første tal, og y-koordinaten er det andet tal efter decimalpunktet. Hver x-koordinat på en linje har en tilsvarende y-koordinat. 
x1: 2 y1: 4 x2: 6 y2: 6 
Oprindelige pointer: (2.4) og (6.6). Anvend på punkt-hældningsformlen: 
Forenkle for det endelige svar:  = hældning
= hældning



Med denne metode skal du stille dig selv følgende spørgsmål: "Hvad er linjens hældning  i punkt (4.2)?"
i punkt (4.2)?" Den afledte skrives ofte som ![Bestemmelse af hældningen af en linje f` src=]() eller
eller 
4 x + 6 

Bestemmelse af hældningen af en linje
Indhold
Hældningen af en linje er et mål for, hvor hurtigt linjen ændrer sig. Dette kan gøres med en lige linje -- hvor hældningen fortæller dig præcis, hvor langt op (positiv hældning) eller ned (negativ hældning) en linje går over en vis afstand. Hældningen kan også bruges til en tangent til en kurve. Eller det kunne være en buet linje, brugt i analyse, hvor hældningen også er kendt som `afledet` af en funktion. I hvert fald, tænk bare på hældningen som "ændringshastigheden" af en graf: hvis variablen "x" bliver større, med hvilken hastighed ændres "y"?? Det er en måde at tænke hældningen på som en årsag og virkning.
Trin
Metode 1 af 3: Find hældningen af en lineær ligning

1. Brug hældningen til at bestemme, hvor stejl og i hvilken retning (op eller ned), en linje går. At bestemme hældningen af en linje er let, så længe du har eller kan tegne en lineær ligning. Denne metode virker kun når:
- Variablerne har ingen eksponenter.
- Der er kun to variable, og ingen af dem er brøker (f.eks. kan følgende ikke være:
)
- Ligningen kan forenkles til formen
, hvorved m og b konstanter (tal såsom 3, 10, -12,
).
2. Find tallet før x, normalt skrevet som `m` for at bestemme hældningen. Hvis ligningen allerede er i den rigtige form,  , så skal du bare vælge tallet i `m`-positionen (men hvis der ikke er et tal før x, er hældningen 1). Så det er også hældningen! Ved, at dette nummer, m, ganges altid med variablen, i dette tilfælde et `x`. Tjek følgende eksempler:
, så skal du bare vælge tallet i `m`-positionen (men hvis der ikke er et tal før x, er hældningen 1). Så det er også hældningen! Ved, at dette nummer, m, ganges altid med variablen, i dette tilfælde et `x`. Tjek følgende eksempler:
 , så skal du bare vælge tallet i `m`-positionen (men hvis der ikke er et tal før x, er hældningen 1). Så det er også hældningen! Ved, at dette nummer, m, ganges altid med variablen, i dette tilfælde et `x`. Tjek følgende eksempler:
, så skal du bare vælge tallet i `m`-positionen (men hvis der ikke er et tal før x, er hældningen 1). Så det er også hældningen! Ved, at dette nummer, m, ganges altid med variablen, i dette tilfælde et `x`. Tjek følgende eksempler:




3. Genkend ligningen, hvor en variabel er isoleret, hvis hældningen ikke er klar. Du kan tilføje, trække fra, gange osv. at isolere en variabel (normalt `y`et`). Husk, at uanset hvad du gør på den ene side af lighedstegnet (såsom at tilføje 3), skal du også gøre dette på den anden side. Dit ultimative mål er en ligning, f.eks  . For eksempel:
. For eksempel:
 . For eksempel:
. For eksempel:
 :
:



Metode 2 af 3: Bestemmelse af hældningen med to punkter

1. Brug en graf og to punkter til hurtigt at finde hældningen uden ligningen. Hvis du har en graf og en linje, men ingen ligning, kan du stadig bestemme hældningen med lethed. Alt du behøver er to punkter på linjen, som du anvender på ligningen  . Når du bestemmer hældningen, skal du huske følgende oplysninger for at sikre dig, at du er på rette vej:
. Når du bestemmer hældningen, skal du huske følgende oplysninger for at sikre dig, at du er på rette vej:
 . Når du bestemmer hældningen, skal du huske følgende oplysninger for at sikre dig, at du er på rette vej:
. Når du bestemmer hældningen, skal du huske følgende oplysninger for at sikre dig, at du er på rette vej: - Positive skråninger går op og til højre.
- Negative skråninger går ned og til højre.
- Stejlere skråninger er stejlere linjer. Mindre stejle skråninger er altid mere gradvise.
- Perfekte vandrette linjer har en hældning på nul.
- Perfekt lodrette linjer har ingen hældning overhovedet. Deres hældning (eller hældning) er `udefineret`.

2. Vælg to punkter, og sæt dem i den simple (x, y) form. Brug grafen (eller opgavespørgsmålet) til at finde x- og y-koordinaterne for to punkter på grafen. De kan bestå af to vilkårlige punkter, linjen passerer igennem. Antag for eksempel, at linjen i denne metode går gennem punktet (2.4) og gennem (6.6).

3. Mærk punkterne x1, y1, x2, y2, og behold hvert punkt med sit par. Fortsæt med vores første eksempel ved at bruge punkterne (2.4) og (6.6), mærke x- og y-koordinaterne for hvert punkt. Hvis alt gik godt, ender du nu med:

4. Erstat disse punkter i `punkt-hældningsformlen` for at finde hældningen. Følgende formel bruges til at bestemme hældningen ved hjælp af to punkter på en lige linje:  . Du skal bare erstatte de fire punkter og forenkle:
. Du skal bare erstatte de fire punkter og forenkle:
 . Du skal bare erstatte de fire punkter og forenkle:
. Du skal bare erstatte de fire punkter og forenkle:
 = hældning
= hældning
5. Forstå, hvordan punkt-hældningsformlen fungerer. Hældningen af en linje er angivet ved ændringen af y fra x (y/x): hvor meget linjen går op divideret med hvor meget linjen fortsætter til højre. Stigningen af linjen er forskellen mellem y-værdierne (husk, y-aksen går op og ned), og stigningen af linjen er forskellen mellem x-værdierne (og x-aksen går fra venstre mod højre).

6. Lær andre måder, du skal vide for at bestemme hældningen. Hældningens ligning er  . Dette kan også repræsenteres af det græske bogstav `Δ` (`delta`), der betyder `forskel`. Hældning kan også repræsenteres som Δy/Δx, hvilket betyder `forskel på y` / `forskel på x`. Dette er præcis det samme spørgsmål som "Bestem hældningen mellem.."
. Dette kan også repræsenteres af det græske bogstav `Δ` (`delta`), der betyder `forskel`. Hældning kan også repræsenteres som Δy/Δx, hvilket betyder `forskel på y` / `forskel på x`. Dette er præcis det samme spørgsmål som "Bestem hældningen mellem.."
 . Dette kan også repræsenteres af det græske bogstav `Δ` (`delta`), der betyder `forskel`. Hældning kan også repræsenteres som Δy/Δx, hvilket betyder `forskel på y` / `forskel på x`. Dette er præcis det samme spørgsmål som "Bestem hældningen mellem.."
. Dette kan også repræsenteres af det græske bogstav `Δ` (`delta`), der betyder `forskel`. Hældning kan også repræsenteres som Δy/Δx, hvilket betyder `forskel på y` / `forskel på x`. Dette er præcis det samme spørgsmål som "Bestem hældningen mellem.."Metode 3 af 3: Brug differentialregning til at finde hældningen af en kurve

1. Gennemgå, hvordan du kan bestemme den afledede af almindelige funktioner på forskellige måder. Derivater giver dig ændringshastigheden (eller hældningen) på et punkt på en linje. Linjen kan være buet eller lige – det er lige meget. Husk, hvordan linjen ændrer sig til enhver tid, i stedet for hvordan hældningen på hele linjen ændres. Hvordan du bestemmer den afledede, afhænger af typen af funktion, så gennemgå, hvordan du bestemmer den afledede af funktioner, før du fortsætter.
- Læs her om at bestemme den afledte
- De simpleste afledte, dem til standardeksponentialligninger, kan du nemt finde med en hurtig metode. Du vil bruge dette i resten af metoden.

2. Forstå hvilke problemer der kræver, at du beregner hældningen ved hjælp af afledte. Du bliver ikke altid eksplicit bedt om den afledede eller hældning af en kurve. Du kan også blive spurgt om `ændringshastigheden` ved punkt (x, y). Du kan blive bedt om en ligning for grafens hældning, hvilket blot betyder at finde den afledede. Til sidst kan du blive bedt om `hældningen af tangentlinjen i (x, y)`. Det betyder igen, at den kun spørger efter kurvens hældning på et bestemt punkt (x, y).
 i punkt (4.2)?"
i punkt (4.2)?"
3.Find den afledede af funktionen. Du behøver ikke engang en rigtig graf, kun grafens funktion eller ligning. I dette eksempel bruger vi en tidligere omtalt funktion,


4.Erstat punktet i den afledede ligning for at finde hældningen. Differentialet for en funktion giver dig hældningen af funktionen på et givet punkt. Med andre ord, f"(x) er hældningen af funktionen til enhver tid (x,f(x)). Så til dette træningsproblem:
Artikler om emnet "Bestemmelse af hældningen af en linje"
Оцените, пожалуйста статью
Lignende
Populær