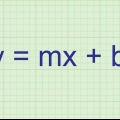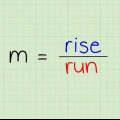Find ligningen af en linje

Indhold

Trin

For at finde ligningen for en linje, du har har brug for to ting:a) et punkt på linjen; og b) linjens hældning (nogle gange også hældningen). Men hvordan du indsamler disse to oplysninger, og hvad du gør med dem bagefter, kan være meget forskelligt afhængigt af situationen. For nemheds skyld vil denne artikel fokusere på formens ligninger y = mx + b i stedet for (å - å₁) = m(x - x₁).

Trin

Metode 1 af 5: Generel information

1. Ved, hvad du skal kigge efter.Før du kan lede efter sammenligningen, skal du vide med sikkerhed, hvad du prøver at finde. Husk følgende:

Point klassificeres som bestilte par, som (-7, -8) eller (-2,-6).
Det første tal i et bestilt par er x koordinat. Dette er punktets vandrette position (hvor mange enheder til venstre eller højre for oprindelsen).
Det andet tal i et bestilt par er y koordinere. Dette er punktets lodrette position (hvor mange enheder op eller ned fra oprindelsen).
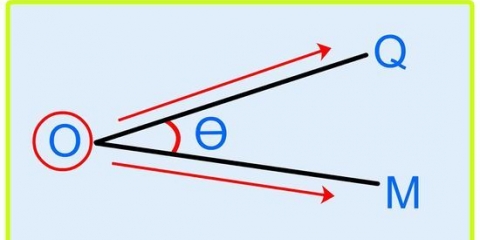
Det hældning mellem de to punkter kaldes "skråningen" - med andre ord, hvor langt du skal gå op (eller ned) og til højre (eller venstre) for at komme fra et punkt til et andet.
To linjer er parallel hvis de ikke krydser hinanden.
To linjer er vinkelrette på hinanden hvis de skærer hinanden i en ret vinkel (90 grader).

2. Bestem, hvilken type opgave du beskæftiger dig med.

Der er givet et punkt og en hældning.

Der gives to point, men ingen hældning.

Givet et punkt og en anden linje parallelt med det.

Givet et punkt og en anden linje vinkelret på det.

3. Løs problemet ved hjælp af en af de fire metoder nedenfor. Afhængigt af de givne oplysninger er der forskellige måder at løse det på.

Metode 2 af 5: Et punkt og en hældning er givet

Billede med titlen Find ligningen af en linje Trin 4

1. Find skæringspunktet mellem din ligning og y-aksen. Skæringspunktet med y-aksen (eller variablen b i vores ligning) er det punkt, hvor linjen skærer y-aksen. Du kan beregne skæringspunktet med y-aksen ved at omarrangere ligningen for at løse for b. Vores nye ligning ser nu sådan ud: b = y - mx.

Indtast din hældning og koordinater i ligningen ovenfor.
Gang hældningen (m) med punktets x-koordinat.
Træk denne værdi fra punktets y-koordinat.
Nu har du b løst, skæringspunktet med y-aksen.

Billede med titlen Find ligningen af en linje Trin 5

2. Skriv formlen ud:y = ____ x + ____ , sammen med de tomme felter.

Billede med titlen Find ligningen af en linje Trin 6

3. Udfyld det første tomme felt, det for x, med hældningen.

Billede med titlen Find ligningen af en linje Trin 7

4. Udfyld det andet felt med skæringspunktet med y-aksen som du har beregnet før.

Billede med titlen Find ligningen af en linje Trin 8

5. Løs eksempelproblemet. "Givet punktet (6, -5) og hældningen 2/3, hvad er ligningen for linjen?"

Omarranger din ligning. b = y - mx.

Indtast værdierne og løs.

b = -5 - (2/3)6.

b = -5 - 4.

b = -9

Tjek, at skæringen med y-aksen virkelig er -9.

Skriv ligningen ned: y = 2/3 x - 9

Metode 3 af 5: To point gives

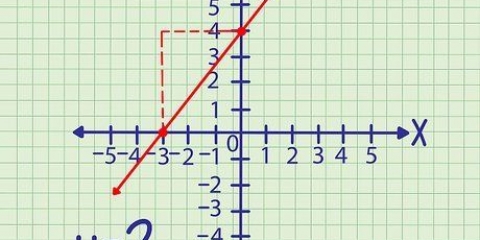
1. Beregn hældningen mellem to punkter. Skråningen kaldes også hældning og du kan tænke på dette som den hastighed, hvormed noget bevæger sig langs en imaginær y-akse og x-akse. Ligningen for hældningen er: (Y₂ - Y₁) / (X₂ - x₁)

Tag de to punkter og brug dem i ligningen (to koordinater betyder to y-værdier og to x-værdier). Det er lige meget, hvilke koordinater du indtaster først, så længe du gør dette konsekvent. Nogle eksempler:

Points (3, 8) og (7, 12). (Y₂ - Y₁) / (X₂ - x₁) = 12 - 8 / 7 - 3 = 4/4 eller 1.
Points (5, 5) og (9, 2). (Y₂ - Y₁) / (X₂ - x₁) = 2 - 5 / 9 - 5 = -3/4.

Billede med titlen Find ligningen for en linje Trin 10

2. Vælg et sæt koordinater for resten af problemet. Overstrege eller dække det andet sæt koordinater, så du ikke ved et uheld bruger dem.

Billede med titlen Find ligningen for en linje Trin 11

3. Beregn skæringspunktet med y-aksen i din ligning. Omarranger igen formlen y = mx + b for at få en ligning af formen b = y – mx. Det er stadig den samme ligning; du har lige omarrangeret det.

Brug din hældning og koordinater i ligningen ovenfor.

Gang hældningen (m) med punktets x-koordinat.

Træk værdien fra punktets y-koordinat.

du har nu b løst, skæringspunktet med y-aksen.

Billede med titlen Find ligningen af en linje Trin 12

4. Skriv formlen ud:y = ____ x + ____ , inklusive de tomme felter.

Billede med titlen Find ligningen af en linje Trin 13

5. Udfyld det første tomme felt, det for x, med hældningen.

Billede med titlen Find ligningen af en linje Trin 14

6. Udfyld det andet felt med skæringspunktet med y-aksen.

Billede med titlen Find ligningen af en linje Trin 15

7. Løs eksempelproblemet. "Givet punkterne (6, -5) og (8, -12), hvad er ligningen for linjen?"

Beregn hældningen. Hældningen = (Y₂ - Y₁) / (X₂ - x₁)

-12 - (-5) / 8 - 6 = -7 / 2

Hældningen er -7/2 (fra det første punkt til det andet går vi 7 ned og 2 til højre, så hældningen er -7 over 2).

Omarranger din ligning. b = y - mx.

Indtast værdierne og løs.

b = -12 - (-7/2)8.

b = -12 - (-28).

b = -12 + 28.

b = 16

Bemærkning: fordi vi brugte 8`eren til koordinaterne, skal vi også bruge -12.Hvis du bruger 6`eren til dine koordinater, skal du også bruge -5.

Tjek, at dit skæringspunkt med y-aksen virkelig er 16.

Skriv ligningen ned: y = -7/2 x + 16

Metode 4 af 5: Når et punkt og en parallel linje er givet

1. Bestem hældningen af den parallelle linje. Husk at hældningen er koefficienten af x hvorved y har ingen koefficient.

I en ligning som y = 3/4 x + 7, er hældningen 3/4.
I en ligning som y = 3x - 2 er hældningen 3.
I en ligning som y = 3x er hældningen stadig 3.
I en ligning som y = 7 er hældningen nul (fordi der er nul x`er i opgaven).
I en ligning som y = x - 7 er hældningen 1.
I en ligning som -3x + 4y = 8, er hældningen 3/4.

For at finde hældningen af en ligning som denne skal du bare omarrangere den, så den y er isoleret:
4y = 3x + 8
Divider begge sider med 4: y = 3/4x + 2

Billede med titlen Find ligningen af en linje Trin 17

2. Beregn skæringspunktet med y-aksen ved hjælp af hældningen fra første trin og ligningen b = y - mx.

Erstat hældningen og koordinaterne i ovenstående ligning.

Gang hældningen (m) med punktets x-koordinat.

Træk værdien fra punktets y-koordinat.

Du har b løst, skæringspunktet med y-aksen.

Billede med titlen Find ligningen af en linje Trin 18

3. Skriv formlen ned:y = ____ x + ____ , med de tomme felter.

Billede med titlen Find ligningen af en linje Trin 19

4. Udfyld det første tomme felt, før x`et, med den hældning, du bestemte i trin 1.Det bemærkelsesværdige ved parallelle linjer er, at de har samme hældning, så man ender med det, man startede med.

Billede med titlen Find ligningen for en linje Trin 20

5. Udfyld skæringspunktet med y-aksen i det andet tomme rum.

6. Løs eksempelproblemet. "Givet punktet (4, 3) og den parallelle linje 5x - 2y = 1; hvad er linjens ligning?"

Løs hældningen. Hældningen på vores nye linje vil være den samme som hældningen på den gamle linje. Bestem hældningen af den gamle linje:

-2y = -5x + 1

trække "-2" af fra begge sider: y = 5/2x - 1/2

Hældningen er 5/2.

Omarranger din ligning. b = y - mx.

Udfyld og løs.

b = 3 - (5/2)4.

b = 3 - (10).

b = -7.

Tjek, om skæringspunktet med y-aksen virkelig er -7.

Skriv ligningen ned: y = 5/2 x - 7

Metode 5 af 5: Med et givet punkt og en vinkelret linje

1. Find hældningen af den givne linje. Se eksemplerne ovenfor for mere information.

Billede med titlen Find ligningen af en linje Trin 23

2. Find den negative gensidige af denne hældning. Med andre ord, vend det om og skift skiltet. Pointen med vinkelrette linjer er, at de har en negativ omvendt hældning, så du bliver nødt til at foretage ændringer af hældningen, før du kan bruge den.

2/3 bliver til -3/2

-6/5 bliver til 5/6

3 (eller 3/1 — er det samme) bliver -1/3

-1/2 bliver til 2