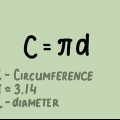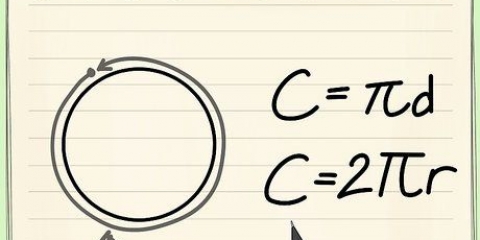Selv π-knappen på en lommeregner bruger ikke den nøjagtige værdi af π, selvom den er nøjagtig nok. 
C er bare en kortere måde at skrive `omkreds` på. 
Du har muligvis skrevet venstre side som π2r, hvilket også er korrekt. Folk kan godt lide at sætte tallene før symbolerne for at gøre ligningen nemmere at læse, men det ændrer ikke resultatet af ligningen. I en matematisk ligning kan du altid gange venstre og højre side med det samme beløb og stadig få en korrekt ligning. 
For eksempel, hvis radius er to enheder lang, så er 2πr = 2 x (3,14) x (2 enheder) = 12,56 enheder = omkredsen. I det samme eksempel, men ved at bruge π-knappen på en lommeregner for bedre nøjagtighed, får du 2 x π x 2 enheder = 12,56637... enheder, men medmindre din lærer har instrueret andet, kan du afrunde tallet til 12,57 enheder. 

Vi bruger d`, ikke2r, fordi dit matematikopgave fortæller dig hvad d midler. Det er dog vigtigt at forstå dette trin, så du ikke bliver forvirret, hvis din lærer eller matematik bog 2r bruges hvor du har en d ville forvente. 
Selv π-knappen på en lommeregner bruger ikke den nøjagtige værdi af π, selvom den er meget nøjagtig. 

π x d = (C/d) x d πd = C 
For eksempel, hvis diameteren er seks, får du (3,14) x (6) = 18,84. I det samme eksempel, men ved at bruge en lommeregners π-knap for mere nøjagtighed, får du π x 6 = 18,84956... men med mindre andet er angivet, kan du afrunde tallet til 18,85. 


A = r A / π = πr / π = r √(A/π) = √(r) = r r = √(A/π) 
C = 2πr C = 2π(√(A/π)) 
Svaret for dette eksempel er 13.72937... men med mindre andet er angivet, kan du runde svaret til 13,73. 


Sørg for at vikle snoren omkring den mere end én gang. Du bør ende med en enkelt løkke, så der ikke er nogen del af cirklen, hvor rebet er dobbeltviklet. 

At finde omkredsen af en cirkel
Indhold
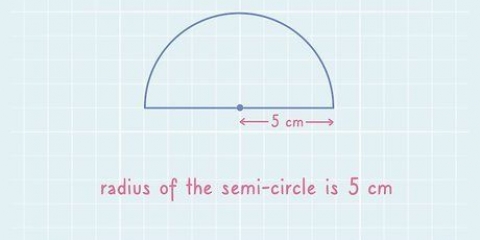
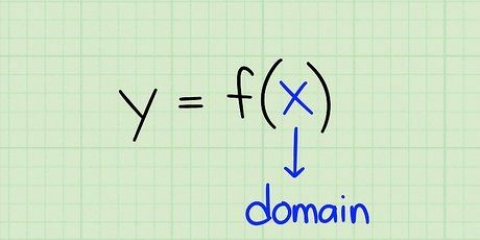
Omkredsen af en cirkel er afstanden rundt om dens kant. Hvis en cirkel har en omkreds på 2 miles, så skal du gå rundt om cirklen 2 miles, før du vender tilbage til hvor du startede. Men hvis du arbejder på et geometrisk problem, behøver du ikke at rejse dig fra stolen. Læs opgaven omhyggeligt for at finde ud af, om `radius` (r), `diameter` (d) eller `areal` (A) af cirklen er givet, og find derefter den del af denne artikel, der er beregnet til at hjælpe dig med opgaven. Der er også instruktioner til at finde omkredsen af et eksisterende cirkulært objekt, du vil måle.
Trin
Metode 1 af 4: Bestemmelse af omkreds ved hjælp af radius

1. Tegn en `stråle` på cirklen. Tegn en linje fra midten af cirklen til en hvilken som helst position på kanten af cirklen. Denne linje er `radius` af cirklen, ofte skrevet som `r` i matematiske ligninger og formler.
- `Bemærkning: hvis radius ikke er angivet i matematikopgaven, så er disse muligvis ikke de rigtige instruktioner. Se, om dem om diameteren eller overfladen er mere nyttige til opgaven.

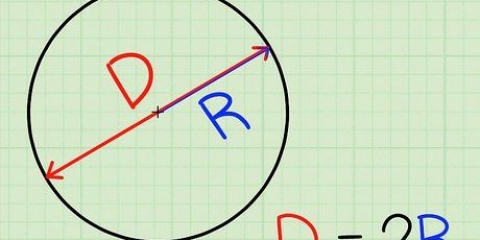
2. Tegn en `diameter` over cirklen. Forlæng den linje, du lige har tegnet, så den når cirkelkanten på den anden side. Du har lige tegnet en anden stråle. De to tilføjede radier har en længde på `2 x radius`, skrevet som 2r. Længden af denne linje er `diameteren` af cirklen, ofte skrevet som d.

3. Forstå π (`pi`). Symbolet π, også skrevet som pi er ikke et magisk tal, der tilfældigvis bliver brugt i den slags matematikopgaver. Faktisk blev tallet π oprindeligt `opdaget` ved at måle cirkler: hvis du måler omkredsen af en cirkel (for eksempel med et målebånd), og derefter dividerer med diameteren, ender du altid med det samme tal. Dette tal er usædvanligt, fordi det ikke kan skrives som en simpel brøk eller decimal. I stedet kan vi runde det op til et tal som 3,14, hvilket er "godt nok".

4. Skriv definitionen af π som et algebraproblem. Som forklaret ovenfor betyder π bare `tallet du får, når du dividerer omkredsen med diameteren`. I form af en matematisk formel er dette: π = C/d. Da vi ved, at diameteren er lig med 2 x radius, kan vi også skrive dette som π = C / 2r.

5. Skift dette problem, så du løser dette problem for perimeter C. Vi vil gerne vide, hvad omkredsen er (C i denne matematiske opgave). Hvis du ganger begge sider med 2r du får π x 2r = (C / 2r) x 2r, og det er det samme som 2πr = C.

6. Erstat de tal, der skal løses, med C. Nu ved vi det 2πr = C. Vend tilbage til det oprindelige matematiske problem for at se hvad r (radius) er. Erstat derefter π med 3,14, eller brug π-knappen på din lommeregner for at få et mere præcist svar. Beregn 2πr med disse tal. Svaret du får er omkredsen.
Metode 2 af 4: Bestemmelse af omkreds ved hjælp af diameteren

1. Forstå, hvad en `diameter` er. Placer din blyant på kanten af cirklen. Tegn en streg gennem midten af cirklen og kanten på den anden side. Denne linje (fra kant til kant og gennem midten) er `diameteren` af cirklen, ofte skrevet som d i matematikopgaver.
- Linjen går gennem det nøjagtige centrum af cirklen, ikke bare hvor som helst i cirklen.
- Bemærkning: Hvis udsagnet ikke angiver, hvor lang diameteren er, skal du bruge en anden metode.

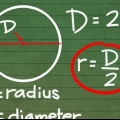
2. Lær, hvad d = 2r betyder. Cirklens `radius`, også skrevet som r, er afstanden fra centrum til kanten af cirklen. Da diameteren går gennem cirklen fra kant til kant, gennem midten, er diameteren lig med to radier. En nem måde at skrive dette på er d = 2r. Det betyder, at du d kan altid erstatte med 2r i en matematikopgave og omvendt.

3. Forstå π (`pi`). Symbolet π, også skrevet som pi er ikke et magisk tal, der tilfældigvis bliver brugt i den slags matematikopgaver. Faktisk blev tallet π oprindeligt `opdaget` ved at måle cirkler: hvis du måler omkredsen af en cirkel (for eksempel med et målebånd), og derefter dividerer med diameteren, ender du altid med det samme tal. Dette tal er usædvanligt, fordi det ikke kan skrives som en simpel brøk eller decimal. I stedet kan vi runde det op til et tal som 3,14, hvilket er "godt nok".

4. Skriv definitionen af π som et algebraproblem. Som forklaret ovenfor betyder π bare `tallet du får, når du dividerer omkredsen med diameteren`. I form af en matematisk formel er dette: π = omkreds / diameter eller π = C/d.

5. Skift dette problem, så du løser dette problem for perimeter C. Vi vil gerne vide, hvad omkredsen er, så vi skal kun have C på den ene side. Gør dette ved at gange hver side af ligningen med d:

6. Erstat tallene og løs for C. Vend tilbage til den oprindelige opgave for at se, hvad diameteren er, og erstat d`et i denne ligning med det tal. Erstat π med en afrunding som 3,14, eller brug π-knappen på din lommeregner for at få et mere præcist resultat. Multiplicer værdierne og d sammen, og du får omkredsen C.
Metode 3 af 4: Find omkredsen ved hjælp af området

1. Forstå, hvordan arealet af en cirkel beregnes. Normalt området (-en) af en cirkel, der ikke er målt direkte. I stedet måler du radius (r) af cirklen, og beregn derefter arealet med formlen A = r. Grunden til at denne formel giver mening er lidt svær at forklare, men du kan lære mere gennem dette link hvis du er interesseret og villig til at komme til bunds i noget tungere algebra.
- Bemærkning: Hvis matematikopgaven ikke nævner området af cirklen, skal du muligvis bruge en anden metode end denne artikel.

2. Lær en formel til at beregne omkreds. Omkredsen (C) er afstanden rundt om cirklen. Det beregner du generelt med formlen C=2πr, men fordi vi endnu ikke ved hvad radius (r), bliver vi nødt til at bruge lidt tid på at finde ud af værdien af r før vi kan løse ligningen.

3. Brug arealformlen til at få r på den ene side. Da A = πr, kan vi omarrangere denne formel for at løse for r i stedet for. Hvis du finder nedenstående trin svære at følge, kan du prøve nogle enklere algebraproblemer først eller øve nogle teknikker til at forstå algebra.

4. Skift perimeterformlen ved at bruge det, du fandt. Hver gang du har en ligning som r = √(A/π), kan du erstatte den ene side af ligningen med den anden?. Lad os bruge denne teknik til at få ovenstående omkredsformel, C=2πr, at skifte. Til dette problem kender vi ikke værdien af r, men vi kender værdien af A. Lad os ændre det sådan her for at gøre problemet løst:

5. Udskift tallene for at finde omkredsen. Brug området givet i opgaven til at finde omkredsen af omkredsen. Hvis området f.eks-en) af en cirkel er 15 kvadratenheder, udfyld derefter 2π(√(15/π)) ind i din lommeregner. Glem ikke beslagene.
Metode 4 af 4: Bestemmelse af omkredsen af en reel cirkel

1. Brug denne metode til at måle rigtige cirkulære objekter. Du kan måle omkredsen af cirkler, du finder i den virkelige verden, ikke kun i problemer. Prøv det på et cykelhjul, en pizza eller en mønt.

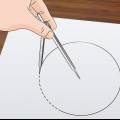
2. Tag et stykke snor og en lineal. Snoren skal være lang nok til at vikle cirklen én gang og fleksibel nok til at passe tæt. Du skal bruge noget til at måle rebet senere, såsom en lineal eller et målebånd. Strengen vil være lettere at måle, hvis linealen er længere end snorens længde.

3. Vikl snoren én gang rundt om cirklen. Start med at placere den ene ende af snoren langs kanten af cirklen. Løft rebet rundt om cirklen og træk det stramt. Hvis du måler en mønt eller en anden tynd genstand, kan du muligvis ikke trække snoren stramt rundt om den. Læg den cirkulære genstand fladt og arranger snoren omkring den, så stram som muligt.

4. Marker eller klip snoren over. Find det sted på snoren, hvor løkken ender, og rør enden af den snor, du startede med. Marker dette sted med en markør, eller klip rebet af på dette sted.

5. Løsn rebet og mål det med en lineal. Tag det omviklede reb og mål det med en lineal. Hvis du brugte en markør, mål kun fra enden af snoren til markøren. Dette er den del af strengen, der vikler sig rundt om cirklen, og da omkredsen af en cirkel kun er afstanden rundt om cirklen, har du fundet svaret! Længden af dette reb er lig med omkredsen af cirklen.
Tips
- Du kan skrive flertal af radius som radius eller som radius.
Artikler om emnet "At finde omkredsen af en cirkel"
Оцените, пожалуйста статью
Populær