Du arbejder nu på en ligesidet trekant, fordi alle tre sider af figuren har nøjagtig samme længde. Men husk, at denne formel gælder for alle trekanter. 
Et andet eksempel: Hvis a = 4, b = 3, og c=5, så er omkredsen 3 + 4 + 5, med andre ord 12. 
I dette eksempel er siderne alle 5 cm, så det rigtige svar er 15 cm. 



For eksempel hvis du kender den silke a = 3 og silke b = 4, så skriv det i formlen sådan her: 3 + 4 = c. Et andet eksempel: Hvis du ved, at længden af sidea = 6, og hypotenusen c = 10, så sætter du det i ligningen sådan her: 6 + b = 10. 
I det første eksempel multiplicerer du værdierne 3 + 4 = c og det opdager du og 25= c. Beregn så kvadratroden af 25, så du kommer frem til c = 25. I det andet eksempel gange du værdierne ind 6 + b = 10 og det opdager du 36 + b = 100.Træk 36 fra 100 for at få b = 64, og beregn så kvadratroden af 64, så du får b = 8. 
I det første eksempel er det X = 3 + 4 + 5 eller 12. I det andet eksempel, dvs X = 6 + 8 + 10 eller 24. 

Forestil dig for eksempel en trekant med en side på 10 og en på 12 og en vinkel på 97° mellem dem. Vi skriver derefter variablerne som følger:a = 10, b = 12, C = 97°. 
c = 10 + 12 - 2 × 10 × 12 × cos(97). c = 100 + 144 – (240 × -0,12187)(Rund cosinus til 5 cifre efter decimaltegnet) c = 244 – (-29,25) c = 244 + 29,25(Tag minustegnet hvis cos(C) er negativ!) c = 273,25 c = 16,53 
I vores eksempel: 10 + 12 + 16,53 = 38,53, det er omkredsen af vores trekant!
Beregning af omkredsen af en trekant
Indhold
Omkredsen af en trekant er længden af en linje, der kan tegnes langs trekantens sider. Den nemmeste måde er at lægge længderne af alle sider sammen, men hvis du ikke kender alle længderne, skal du beregne dem først. Denne artikel lærer dig først, hvordan du beregner omkredsen af en trekant, hvis du kender længderne af alle tre sider; dette er den nemmeste og mest brugte metode. Så lærer du, hvordan du beregner omkredsen, hvis du kun kender længden af to af de tre sider. Til sidst forklares det, hvordan man beregner omkredsen, hvis man kender længden af to sider og vinklen mellem dem ved hjælp af cosinusloven.
Trin
Metode 1 af 3: Beregning af omkredsen af en trekant, hvis længden af alle sider er givet

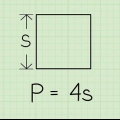
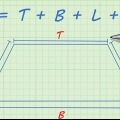
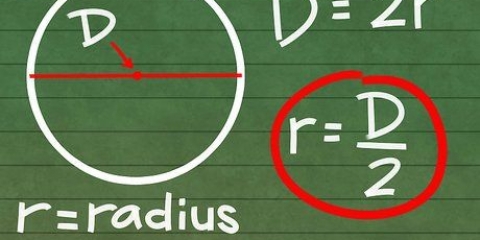
1. Lær formlen til at finde omkredsen. Formlen er: A + B + C = X hvorved -en, B, og C repræsenterer længderne af siderne og x omkredsen.
- Denne formel betyder grundlæggende, at for at finde omkredsen af en trekant, skal du lægge længderne af de tre sider sammen.

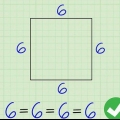
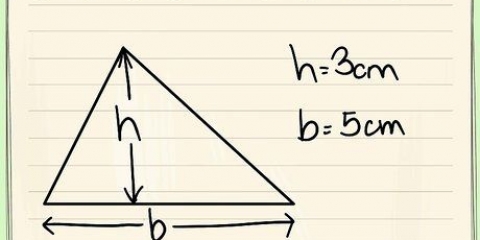
2. Bestem længden af alle tre sider. I dette eksempel: -en = 5, B = 5, C = 5.

3. Læg længderne af de tre sider sammen. I dette eksempel: 5 + 5 + 5 = 15. Så omkredsen af trekanten (X) er 15.

4. Husk altid at medtage enhederne i din besvarelse. Hvis siderne er angivet i centimeter, skal dit endelige svar også angives i centimeter. Hvis siderne er givet i form af en variabel, for eksempel x, så skal svaret også være i form af x.
Metode 2 af 3: Beregning af omkredsen, hvis kun to sider af trekanten er givet

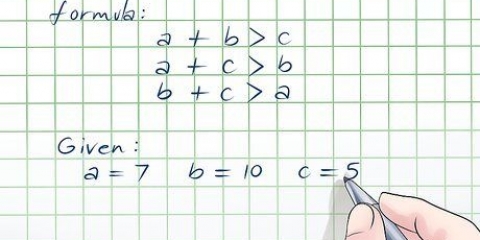
1. Ved hvad en retvinklet trekant er. En retvinklet trekant er en trekant med en ret vinkel (90 grader). Siden af trekanten modsat den rette vinkel er altid den længste side, som kaldes hypotenusen eller hypotenusen. Retvinklede trekanter dukker jævnligt op i matematikprøver, men heldigvis er der en meget praktisk formel til at beregne længden af ukendt side!

2. Kend Pythagoras sætning. Pythagoras sætning gælder for enhver retvinklet trekant og lyder: a² + b² = c².

3. Se på din trekant og skriv ved siderne -en, b og c. Husk at den længste side kaldes hypotenusen. Den er placeret modsat den rigtige vinkel, og du skal gå til denne side c at skrive. På de to kortere sider skriver du -en og b. Det er lige meget, hvilken du placerer hvor, resultatet bliver det samme!

4. Tag længderne af siderne i Pythagoras sætning. Huske på, at a + b = c. Udfyld længderne i stedet for de tilsvarende bogstaver.

5. Løs ligningen for at finde den manglende længde. Du skal først gange de kendte sider med sig selv (for eksempel 3 = 3 * 3 = 9).Hvis du leder efter hypotenusen, kan du så bare lægge de to værdier sammen og beregne kvadratroden af resultatet for at finde længden. Hvis du mangler en anden side, skal du trække de to fra og derefter beregne kvadratroden af resultatet for at finde længden.

6. Læg længderne af de tre sider sammen for at beregne omkredsen. Husk ligningen: X = a + b + c. Nu hvor du kender længderne på siderne-en, b og c ved du kan lægge dem sammen for at få omkredsen.
Metode 3 af 3: Find omkredsen af en trekant ved hjælp af cosinusloven

1. Lær cosinusloven. Ved hjælp af cosinusloven kan du løse enhver trekant, hvis du kender længden af to sider og vinklen mellem dem. Det virker for enhver trekant, og det er en meget nyttig formel. Cosinusloven siger, at for enhver trekant med sider -en, b, og c, med modsatte hjørner-en, B, og C følgende formel gælder:c = a + b - 2ab cos(C).

2. Se på din trekant og sæt bogstaverne ved de forskellige dele. Den første side ved du, du skal -en kalder det, og den modsatte vinkel er derefter -en. Den anden side ved du, du skal b ring til det modsatte hjørne B. Den vinkel, du ved, du skal C kald det, og den tredje side, den du vil løse, er derefter c.

3. Indsæt dine oplysninger i ligningen og løs for side c. Du skal først gange a og b med sig selv og lægge dem sammen. Beregn derefter cosinus af C med cos-funktion på din lommeregner eller en online lommeregner. Formere sig cos(C) af 2ab og trække resultatet fra summen af a + b.Svaret er c.Beregn kvadratroden af dette, og du kender længden af siden c.I vores eksempel:

4. Brug længden afc for at beregne omkredsen af din trekant. Husk at formlen for omkredsen er: X = a + b + c, så du skal bare lægge alle længderne sammen pga -en og b vidste du.Et stykke kage!
Artikler om emnet "Beregning af omkredsen af en trekant"
Оцените, пожалуйста статью
Lignende
Populær