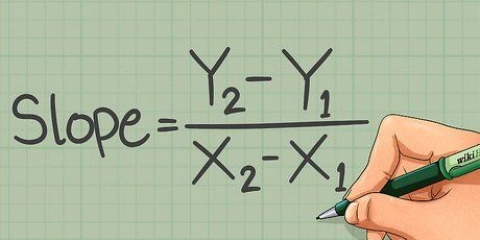Sådan bestemmer du, om tre længder sammen danner en trekant: 6 trin (med billeder)

Indhold

Trin
Tips

Det er nemmere at afgøre, om længderne af tre sider tilsammen danner en trekant, end det ser ud. Alt du skal gøre er at bruge Trekantulighedssætningen, som siger, at summen af længderne af to sider af en trekant altid er større end den tredje side. Hvis dette gælder for alle tre kombinationer af de tilføjede længder, så har du at gøre med en trekant.

Trin

1. Lær sætningen om trekantens ulighed. Denne sætning siger, at summen af to sider i en trekant skal være større end den tredje side. Hvis dette gælder for alle tre kombinationer, så har du en sand trekant. Du bliver nødt til at kontrollere disse kombinationer, én efter én, for at sikre, at en trekant kan dannes. Du kan også betragte trekanten som siderne af længderne a, b og c, og sætningen som ulighed: a+b > c, a+c > b og b+c > -en.

Et eksempel, -en = 7, b = 10 og c = 5.

Billede med titlen Bestem, om tre sidelængder er en trekant Trin 2

2. Tjek om summen af de to første sider er større end den tredje. I dette tilfælde kan du bruge siderne -en og b læg sammen, dvs. 7 + 10, for at få 17, hvilket er større end 5. Du kan også tænke på det som 17 > 5.

Billede med titlen Bestem, om tre sidelængder er en trekant Trin 3

3. Tjek om summen af den næste kombination af to sider er større end den resterende side. Nå, bare se om summen af siderne -en og c er større end siden b. Det betyder, at du skal se, om 7 + 5 eller 12 er større end 10. 12 > 10, så det er rigtigt.

Billede med titlen Bestem, om tre sidelængder er en trekant Trin 4

4. Tjek om summen af den sidste kombination af to sider er større end den resterende side. Du bliver nødt til at kontrollere, om summen af sider b og silke c er større end silke -en. For at gøre dette skal du kontrollere, om 10 + 5 er større end 7. 10 + 5 = 15 og 15 > 7, så trekanten er korrekt for alle sider.

Billede med titlen Bestem, om tre sidelængder er en trekant Trin 5

5. Tjek dit arbejde. Nu hvor du har markeret alle sider én efter én, kan du igen kontrollere, at reglen gælder for alle tre kombinationer. Hvis summen af en af de to sider er større end den tredje i enhver kombination, som med denne trekant, så har du bestemt, at trekanten er gyldig. Hvis reglen ikke gælder for en enkelt kombination, er det ikke en sand trekant. Da følgende udsagn er sande, har du fundet en gyldig trekant:

a + b > c = 17 > 5

a + c > b = 12 > 10

b + c > -en = 15 > 7

Billede med titlen Bestem, om tre sidelængder er en trekant Trin 6

6. Vide, hvordan man finder ud af en ugyldig trekant. Bare for at få styr på det, men du skal sikre dig, at du kan få øje på en trekant, der ikke er rigtig. Antag, at du har at gøre med følgende tre sider og længderne: 5, 8 og 3. Lad os se, om de består testen:

5 + 8 > 3 = 13 > 3, så denne side er korrekt.

5 + 3 > 8 = 8 > 8. Fordi det ikke er i orden, kan du stoppe nu. Dette er ikke en trekant.