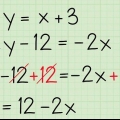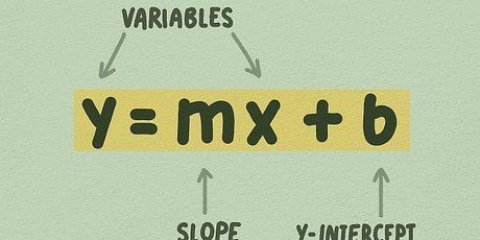Punkter er nemme at bestemme, hvis du har tegnet en streg på millimeterpapir. For at bestemme et punkt skal du tegne en stiplet linje op fra den vandrette akse, indtil den skærer linjen. Den position, hvor du startede linjen på den vandrette akse, er x-koordinaten, mens y-koordinaten er, hvor den stiplede linje skærer linjen på den lodrette akse. For eksempel: linje l har punkterne (1, 5) og (-2, 4) mens linje r har punkterne (3, 3) og (1, -4). 
Til linjens hældning l at beregne: hældning = (5 - (-4))/(1 - (-2)) Træk fra: hældning = 9/3 Divider: hældning = 3 Linjens hældning r = (3 - (-4))/(3 - 1) = 7/2 
I dette eksempel er 3 ikke lig med 7/2, så disse to linjer er ikke parallelle. 

For eksempel: Omskriv linjen 4y-12x=20 som hældningsformel. Tilføj 12x til begge sider af ligningen: 4y - 12x + 12x = 20 + 12x Divider hver side med 4 for at isolere y: 4y/4 = 12x/4 +20/4 Hældningsformel: y = 3x + 5 
I vores eksempel har den første linje ligningen y = 3x + 5, så hældningen er 3. Den anden linje har en ligning på y = 3x - 1, som også har en hældning på 3. Da skråningerne er identiske, er disse to linjer parallelle. Bemærk, at hvis disse ligninger har samme skæring med y-aksen, ville de være den samme linje i stedet for parallelle. 

Linjen vi ønsker at gøre parallel er y = -4x + 3. I denne ligning repræsenterer -4 variablen m og dermed linjens hældning. 
I vores eksempel bruger vi koordinaten (1, -2). 
Ved at bruge vores eksempel med hældning (m) -4 og (x, y) koordinat (1, -2) bliver dette: y – (-2) = -4(x – 1) 
For eksempel: y - (-2) = -4(x - 1) To negativer gør en positiv: y + 2 = -4(x -1) Brug fordelingsegenskaben for at beregne -4(x -1): y + 2 = -4x + 4. Træk -2 fra begge sider: y + 2 - 2 = -4x + 4 - 2 Den forenklede ligning: y = -4x + 2
Bestem om to linjer er parallelle
Indhold
Parallelle linjer er to linjer i et plan, der aldrig vil skære hinanden (hvilket betyder, at de vil fortsætte for evigt uden nogensinde at røre). Et vigtigt kendetegn ved parallelle linjer er, at de har identiske hældninger. Hældningen af en linje er defineret som stigningen (ændring i y-koordinater) over faldet (ændring i x-koordinater) af en linje, med andre ord hvor stejl linjen er. Parallelle linjer er ofte repræsenteret af to lodrette linjer (ll). For eksempel angiver AB11CD, at linje AB er parallel med CD.
Trin
Metode 1 af 3: Sammenligning af hver linjes hældning

1. Find formlen for hældningen. Hældningen (hældningen) af en linje er defineret af (Y2 - Y1)/(X2 - x1) hvor X og Y er de vandrette og lodrette koordinater for punkter på linjen. Du skal bestemme to punkter på linjen for at beregne denne formel. Punktet tættere på bunden af linjen er (X1, Y1) og punktet højere op på linjen, over det første punkt, er (X2, Y2).
- Denne formel kan omformuleres som stigningen over afstanden. Det er den lodrette ændring i forhold til den vandrette ændring, eller linjens stejlhed.
- Hvis en linje peger til højre og op, vil den have en positiv hældning.
- Hvis linjen peger til højre og ned, vil den have en negativ hældning.

2. Identificer X- og Y-koordinaterne for to punkter på hver linje. Et punkt på en linje er givet ved dets koordinat (X, Y), hvor X er placeringen på den vandrette akse og Y er placeringen på den lodrette akse. For at beregne hældningen skal du bestemme to punkter på hver af de pågældende linjer.

3. Bearbejd punkterne for hver linje i hældningsformlen. For at beregne hældningen skal du indtaste tallene, trække fra og dividere. Sørg for at indsætte koordinaterne i den korrekte x- og y-værdi i formlen.

4. Sammenlign hældningerne på hver linje. Husk, at to linjer kun er parallelle, hvis de har samme hældning. Linjer kan forekomme parallelle på papir og endda være meget tæt på parallelle, men hvis deres hældninger ikke er nøjagtigt lige store, er de ikke parallelle.
Metode 2 af 3: Brug af hældnings- og skæringsformlen

1. Find formlen for hældning og skæringspunkt for en linje. Hældningsformlen, ligningen for en ret linje. er y = mx + b, hvor m er hældningen, b er skæringspunktet med y-aksen, og x og y er variabler, der repræsenterer koordinater på linjen - generelt ser du dem som x og y i ligningen. I denne formular kan du nemt bestemme linjens hældning som variablen `m`.
- Et eksempel: omskriv 4y - 12x = 20 og y = 3x -1. Ligningen 4y - 12x = 20 skal omskrives med algebra, mens y = 3x -1 allerede har form af hældningsformlen og ikke skal omskrives.

2. Omskriv formlen for linjen som hældningsformel. Ofte vil formlen for den linje, du får, ikke være i form af et skråplan. Det kræver bare lidt matematik og variabel omarrangering for at få det til hældningsformlen.

3. Sammenlign hældningerne på hver linje. Husk, at hvis to linjer er parallelle med hinanden, vil de have nøjagtig samme hældning. Ved at bruge ligningen y = mx + b, hvor m er linjens hældning, kan du bestemme og sammenligne hældningerne på to linjer.
Metode 3 af 3: Bestemmelse af en parallel linje med punkt-hældningsligningen

1. Definer punkt-hældningsligningen. Med punkt-hældningsligningen kan du skrive ligningen for en linje, hvis du kender hældningen og har en (x, y) koordinat. Du bruger denne formel, hvis du vil definere en anden parallel linje på en allerede given linje med en bestemt hældning. Formlen er y – y1= m(x – x1) hvor m er linjens hældning, x1 x-koordinaten for et givet punkt på linjen og y1 y-koordinaten for det punkt. Som i hældningsformlen er x og y variable, der repræsenterer koordinater på linjen - generelt vil de forblive som x og y i ligningen.
- Følgende trin udarbejder dette eksempel: Skriv ligningen for en linje parallel med linjen y = -4x + 3, der går gennem punkt (1, -2).

2. Find hældningen på den første linje. Når du skriver ligningen for en ny linje, skal du først bestemme hældningen på den linje, som din linje skal være parallel med. Sørg for, at ligningen for den oprindelige linje er en hældningsformel, så du kender hældningen (m) med det samme.

3. Identificer et punkt på den nye linje. Denne ligning virker kun, hvis du har en koordinat, der går gennem den nye linje. Sørg for ikke at vælge en koordinat, der er på den oprindelige linje. Hvis dine endelige ligninger har samme y-skæringspunkt, er de ikke parallelle, men den samme linje.

4. Skriv ligningen for den nye linje i punkthældningsformen. Husk at formlen er: y – y1= m(x – x1). Indtast hældningen og koordinaterne for dit punkt for at gøre ligningen for din nye linje parallel med den første.

5. Forenkle ligningen. Når du har udfyldt tallene, kan ligningen forenkles til den mere almindelige hældningsformel. Linjen i denne ligning, når den tegnes i et koordinatsystem, er parallel med den givne ligning.
Artikler om emnet "Bestem om to linjer er parallelle"
Оцените, пожалуйста статью
Populær