For eksempel har et kredsløb to modstande parallelt, hver med 4Ω modstand. /Rt = /4Ω + /4Ω → /Rt = /2Ω → Rt = 2Ω. Med andre ord er to grene med lige stor modstand nøjagtig dobbelt så nemme at komme igennem som en enkelt gren for sig selv. Hvis en gren ikke har nogen modstand (0Ω), så løber al strøm gennem den gren. Den samlede modstand er da nul. 

Sørg for, at hver værdi refererer til den samme del af kredsløbet. Du kan bruge Ohms lov til at undersøge det samlede kredsløb (V = ItRt) eller en enkelt gren (V = I1R1). 







Rt = R1R2 / (R1 + R2) 
For eksempel giver to identiske parallelle modstande halvdelen af den samlede modstand af en enkelt modstand. Otte identiske modstande giver ⅛ af den samlede modstand. 
To modstande parallelt: I1 = jegtR2 / (R1 + R2) Mere end to parallelle modstande: Om I1 for at bestemme, kigger du efter den kombinerede modstand af alle modstande Næste R1. Husk at bruge formlen for parallelle modstande. Brug derefter ligningen og erstat R2 ved dit svar.
Løsning af parallelle kredsløb
Indhold
Løsning af parallelle kredsløb er en nem proces, når du kender de grundlæggende formler og principper. Når to eller flere modstande er forbundet side om side, kan strømmen "vælge" en vej (meget på samme måde som biler skifter vognbane og kører side om side, når en enkelt kørebane deler sig i to parallelle vognbaner). Efter at have læst disse trin bør du være i stand til at finde spændingen, strømmen og modstanden mellem to eller flere modstande forbundet parallelt.
snydeark
- Total modstand Rt for parallelle modstande: /Rt = /R1 + /R2 + /R3 + ...
- Spændingen er altid den samme over grenene: Vt = V1 = V2 = V3 = ...
- Samlet strøm It = jeg1 + jeg2 + jeg3 + ...
- Ohms lov: V = IR
Trin
Del 1 af 3: Introduktion til parallelle kredsløb

1. Lær at genkende parallelle kredsløb. Et parallelkredsløb har to eller flere grene, der alle fører fra punkt A til punkt B. En enkelt strøm af elektroner deler sig i flere grene og rekombinerer derefter til en strøm på den anden side. De fleste problemer med parallelle kredsløb beder dig om at beregne den samlede spænding, modstand eller strøm over kredsløbet (punkt A til punkt B).
- Dele, der er `forbundet parallelt`, er hver på en separat gren.

2. Forstå strøm og modstand i parallelle kredsløb. Forestil dig en motorvej med flere kørebaner og betalingsanlæg i hver vognbane, der bremser trafikken. Oprettelse af en ny vognbane giver bilerne en anden vej at tage, så det vil fremskynde trafikken, selvom du tilføjer nye betalingsanlæg. Tilsvarende vil tilføjelse af en ny gren til et parallelkredsløb give strømmen en ekstra vej. Det er lige meget, hvor meget modstand den nye gren har; den samlede modstand i kredsløbet vil falde, og den samlede strøm i kredsløbet vil stige.

3. Læg strømmen sammen i hver gren for at få den samlede strøm. Hvis du kender strømmen i hver gren, skal du lægge dem sammen for at få den samlede nuværende strøm. Dette er mængden af strøm, der løber gennem kredsløbet, når alle grene samles. I formelform: It = jeg1 + jeg2 + jeg3 + ...

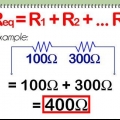
4. Bestem den samlede modstand. For at få den samlede modstand Rt om kredsløbet, brug ligningen /Rt = /R1 + /R2 + /R3 + ... hvor hver R til højre er modstanden over en gren af kredsløbet.

5. Husk det, der beskrives ved spænding. Spænding er forskellen i potentiale mellem to punkter. Da du sammenligner to punkter og ingen strømvej, forbliver spændingen den samme, uanset hvilken gren du ser på. Vt = V1 = V2 = V3 = ...

6. Find de manglende værdier med Ohms lov. Ohms lov beskriver forholdet mellem spænding V, strøm I og modstand R: V = IR. Hvis du kender to af disse værdier, skal du bruge denne formel til at løse den tredje.
Del 2 af 3: Prøvekredsløb

1. Opret et diagram for at spore dit arbejde. Hvis du har et parallelkredsløb med flere ukendte værdier, vil en graf hjælpe med at organisere dine data. Her er et eksempeldiagram af et kredsløb med tre parallelle forgreninger. Bemærk, at grenene ofte er betegnet med R efterfulgt af et tal i sænket skrift.
| R1 | R2 | R3 | i alt | Enheder | |
|---|---|---|---|---|---|
| V | volt | ||||
| jeg | ampere | ||||
| R | ohm |

2. Udfyld alle oplysninger som angivet i erklæringen. For eksempel: vi bruger et kredsløb, der drives af et 12-volts batteri. Kredsløbet har tre parallelle grene med modstande 2Ω, 4Ω og 9Ω. Inkorporer disse oplysninger i dit diagram:
| R1 | R2 | R3 | i alt | Enheder | |
|---|---|---|---|---|---|
| V | 12 | volt | |||
| jeg | ampere | ||||
| R | 2 | 4 | 9 | ohm |

3. Kopier spændingen til hver gren. Husk, at spændingen over hele kredsløbet i et parallelkredsløb er lig med spændingen over hver gren.
| R1 | R2 | R3 | i alt | Enheder | |
|---|---|---|---|---|---|
| V | 12 | 12 | 12 | 12 | volt |
| jeg | ampere | ||||
| R | 2 | 4 | 9 | ohm |

4. Brug Ohms lov til at bestemme strømmen i hver gren. Hver kolonne i dit diagram indeholder en spænding, strøm og modstand. Det betyder, at du altid kan løse en manglende værdi, så længe de to andre værdier i samme kolonne er kendt. Hvis du har glemt det, er Ohms lov V = IR. Den manglende værdi i vores eksempel er strømmen (I), så vi omformulerer den som I = V/R.
| R1 | R2 | R3 | i alt | Enheder | |
|---|---|---|---|---|---|
| V | 12 | 12 | 12 | 12 | volt |
| jeg | 12/2 = 6 | 12/4 = 3 | 12/9 = ~1.33 | ampere | |
| R | 2 | 4 | 9 | ohm |

5. Bestem den samlede strøm. Dette er en let værdi at finde, da den samlede strøm er lig med summen af strømmene i hver gren.
| R1 | R2 | R3 | i alt | Enheder | |
|---|---|---|---|---|---|
| V | 12 | 12 | 12 | 12 | volt |
| jeg | 6 | 3 | 1.33 | 6 + 3 + 1.33 = 10.33 | ampere |
| R | 2 | 4 | 9 | ohm |

6. Løs den samlede modstand. Du kan bestemme dette på to forskellige måder. Du kan bruge rækken af modstandsværdier til at beregne dette ved hjælp af formlen /Rt = /R1 + /R2 + /R3. Det er dog ofte nemmere at løse dette ved hjælp af Ohms lov og de samlede V- og I-værdier. Når du løser for modstand, skal du omformulere Ohms lov som R = V/I.
| R1 | R2 | R3 | i alt | Enheder | |
|---|---|---|---|---|---|
| V | 12 | 12 | 12 | 12 | volt |
| jeg | 6 | 3 | 1.33 | 10.33 | ampere |
| R | 2 | 4 | 9 | 12/10.33 = ~1.17 | ohm |
Del 3 af 3: Yderligere beregninger

1. Beregn kraften. Som i ethvert kredsløb er effekten P = IV. Hvis du har beregnet magten over hver af grenene, så er den samlede effekt Pt lig med summen af alle effektværdier på tværs af grenene (P1 + s2 + s3 + ...).

2. Bestem den samlede modstand over et to-grenet kredsløb. Hvis præcis to modstande er forbundet parallelt, kan du forenkle ligningen til `produktet over summen`:

3. Bestem den samlede modstand, når alle modstande er identiske. Hvis hver parallel modstand har den samme modstandsværdi, bliver ligningen meget enklere. Rt = R1 /N, hvor N er antallet af modstande.

4. Beregn strøm i grene uden spænding. Med denne ligning, Kirchhoffs strømdelerregel, kan du bestemme strømmen for enhver individuel gren, selvom du ikke kender kredsløbsspændingen. Modstanden for hver gren skal være kendt, såvel som den samlede strøm `f` over kredsløbet:
Tips
- For at løse serie- eller parallelkredsløb skal du først løse de parallelle dele. Derefter er dit kredsløb blevet meget nemmere.
- I et parallelkredsløb har alle modstande den samme spænding.
- Du har måske lært Ohms lov, såsom E = IR eller V = AR. Det er bare forskellige notationer for det samme.
- Den samlede modstand omtales også som `ækvivalent med modstanden`.
- Hvis du ikke har en lommeregner, kan du bestemme den samlede modstand fra R1, R2, etc., være vanskelig for nogle kredsløb. Brug i stedet Ohms lov til at bestemme strømmen over hver gren.
Artikler om emnet "Løsning af parallelle kredsløb"
Оцените, пожалуйста статью
Populær