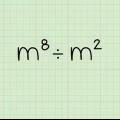Ti til tres magt











Som vist her, kan du fortsætte med at gange grundtallet med produktet af hvert af de første talpar, indtil du får det endelige svar. Fortsæt blot med at gange de første to tal, og gang derefter dette svar med det næste tal i rækkefølgen. Dette gælder for enhver eksponent. Når du er færdig med eksemplet, får du  .
. 




Brug en søgemaskine som Startpage, Duckduckgo eller Google til at finde svaret. Du kan bruge `^`-knappen på din computer, tablet eller smartphone til at indtaste udtrykket i søgefeltet, og du vil straks se svaret og forslag til lignende udtryk at udforske (Duckduckgo viser endda en komplet lommeregner ). 





Da alt er det samme tal, men ganget, kan vi kombinere disse: 




Da baserne er de samme, kan du bare lægge dem sammen: 




Som du vil se om et øjeblik, vil ethvert tal, der er en del af en brøk, som f.eks  , omskrives som
, omskrives som  . Negative eksponenter danner brøker.
. Negative eksponenter danner brøker. 
 = 125
= 125 = 12
= 12 = -x^12
= -x^12 =
=  Husk, at et tal uden potens har en eksponent på 1
Husk, at et tal uden potens har en eksponent på 1 =
= 
 =
= 




![Løsning af eksponenter x^{{{frac{1}{3}}}}={sqrt[ {3}]{x}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/759eade6ce89e27b301ccdcd83d7e8858827b8e2)
 =
= ![Løsning af eksponenter ({sqrt[ {3}]{x}})^{5}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8ea002d6365c3ba2d1d255162136605453a7135f)



Løsning af eksponenter
Indhold
Eksponenter bruges, når et tal ganges med sig selv. I stedet for 



Trin
Metode 1 af 3: Løsning af simple eksponenter

1. Lær de korrekte termer og ordforråd til eksponentielle problemer. Har du en eksponent som  , så arbejder du med to simple dele. Stelnummeret her er et 2 eller grundlag. Dette tal hæves til 3 potens, også kendt som eksponent eller strøm. taler vi om
, så arbejder du med to simple dele. Stelnummeret her er et 2 eller grundlag. Dette tal hæves til 3 potens, også kendt som eksponent eller strøm. taler vi om  , så siger vi `to til den tredje`, `to til den tredje potens` eller `to rejser til den tredje potens`.`
, så siger vi `to til den tredje`, `to til den tredje potens` eller `to rejser til den tredje potens`.`
 , så arbejder du med to simple dele. Stelnummeret her er et 2 eller grundlag. Dette tal hæves til 3 potens, også kendt som eksponent eller strøm. taler vi om
, så arbejder du med to simple dele. Stelnummeret her er et 2 eller grundlag. Dette tal hæves til 3 potens, også kendt som eksponent eller strøm. taler vi om  , så siger vi `to til den tredje`, `to til den tredje potens` eller `to rejser til den tredje potens`.`
, så siger vi `to til den tredje`, `to til den tredje potens` eller `to rejser til den tredje potens`.` - Hvis et tal hæves til anden potens, som f.eks
, så kan man også sige, at tallet er firkantet er ligesom `fem i kvadrat.`
- Hvis et tal hæves til tredje potens, som f.eks
, så kan man også sige det tal a terning nummer er.
- Hvis et tal uden eksponent nævnes, som f.eks. 4, så er det teoretisk set i første potens og kan omskrives som
.
- Hvis eksponenten er lig med 0, og et `tal (ikke-nul)` hæves til `nulpotens`, så er hele tallet lig med 1, som
eller endda noget lignende
Mere om dette i afsnittet `Tips`.

2. Multiplicer grundtallet det antal gange for sig selv som angivet af eksponenten. Hvis du skal løse en potens i hånden, starter du med at omskrive den som en multiplikation. Du gange grundtallet antallet af gange med sig selv, som angivet af eksponenten. Så har du  så gange du tre fire gange med sig selv
så gange du tre fire gange med sig selv  . Et par flere eksempler er:
. Et par flere eksempler er:
 så gange du tre fire gange med sig selv
så gange du tre fire gange med sig selv  . Et par flere eksempler er:
. Et par flere eksempler er:



3. Løs et udtryk: Gang de første to tal sammen for at få produktet. For eksempel med  , starter du med
, starter du med  Det virker som en kedelig opgave, men gør det bare trin for trin. Start med at gange de første to firere. Erstat derefter de to firere med svaret som vist nedenfor:
Det virker som en kedelig opgave, men gør det bare trin for trin. Start med at gange de første to firere. Erstat derefter de to firere med svaret som vist nedenfor:
 , starter du med
, starter du med  Det virker som en kedelig opgave, men gør det bare trin for trin. Start med at gange de første to firere. Erstat derefter de to firere med svaret som vist nedenfor:
Det virker som en kedelig opgave, men gør det bare trin for trin. Start med at gange de første to firere. Erstat derefter de to firere med svaret som vist nedenfor:



4. Gang svaret fra det første par (16) med det næste tal. Fortsæt med at gange tallene for at `vokse` din eksponent. Fortsætter vi med vores eksempel, multiplicerer vi 16 med de næste 4, således at:






 .
.
5. Prøv også følgende eksempler, og tjek dine svar med en lommeregner.




6. Brug `exp,` `x n  ` eller `^` knappen på din lommeregner for eksponenterne. Det er næsten umuligt at finde større eksponenter, som f.eks
` eller `^` knappen på din lommeregner for eksponenterne. Det er næsten umuligt at finde større eksponenter, som f.eks  i hånden, men lommeregnere kan nemt klare dette. Knappen til dette er normalt angivet tydeligt nok. Windows-beregneren kan udvides til en videnskabelig lommeregner ved at klikke på lommeregnerens `Vis`-fane og vælge `Videnskabelig`. Hvis du vil have standardberegneren tilbage, skal du klikke på `Vis` igen og vælge `Standard`.
i hånden, men lommeregnere kan nemt klare dette. Knappen til dette er normalt angivet tydeligt nok. Windows-beregneren kan udvides til en videnskabelig lommeregner ved at klikke på lommeregnerens `Vis`-fane og vælge `Videnskabelig`. Hvis du vil have standardberegneren tilbage, skal du klikke på `Vis` igen og vælge `Standard`.
 ` eller `^` knappen på din lommeregner for eksponenterne. Det er næsten umuligt at finde større eksponenter, som f.eks
` eller `^` knappen på din lommeregner for eksponenterne. Det er næsten umuligt at finde større eksponenter, som f.eks  i hånden, men lommeregnere kan nemt klare dette. Knappen til dette er normalt angivet tydeligt nok. Windows-beregneren kan udvides til en videnskabelig lommeregner ved at klikke på lommeregnerens `Vis`-fane og vælge `Videnskabelig`. Hvis du vil have standardberegneren tilbage, skal du klikke på `Vis` igen og vælge `Standard`.
i hånden, men lommeregnere kan nemt klare dette. Knappen til dette er normalt angivet tydeligt nok. Windows-beregneren kan udvides til en videnskabelig lommeregner ved at klikke på lommeregnerens `Vis`-fane og vælge `Videnskabelig`. Hvis du vil have standardberegneren tilbage, skal du klikke på `Vis` igen og vælge `Standard`.Metode 2 af 3: Addere, subtrahere og gange eksponenter

1. Du kan kun addere eller trække potenstal fra hinanden, hvis de har samme grundtal og samme eksponent. Hvis du har at gøre med identiske baser og eksponenter, som f.eks  , så kan du forenkle tilføjelsen af led til en multiplikation. Glem ikke at
, så kan du forenkle tilføjelsen af led til en multiplikation. Glem ikke at  kan betragtes som
kan betragtes som  , så det
, så det  ved at tilføje, hvor `1 af det + 1 af det = 2 af det`, uanset hvad `det` måtte være. Læg blot antallet af ens udtryk (dem med identisk grundtal og eksponent) sammen og multiplicer summen med det eksponentielle udtryk. Det kan du så
ved at tilføje, hvor `1 af det + 1 af det = 2 af det`, uanset hvad `det` måtte være. Læg blot antallet af ens udtryk (dem med identisk grundtal og eksponent) sammen og multiplicer summen med det eksponentielle udtryk. Det kan du så  løse og gange svaret med to. Husk, at dette er muligt, fordi en multiplikation ikke er andet end at omskrive en addition, fordi
løse og gange svaret med to. Husk, at dette er muligt, fordi en multiplikation ikke er andet end at omskrive en addition, fordi  . Her er et par eksempler:
. Her er et par eksempler:
 , så kan du forenkle tilføjelsen af led til en multiplikation. Glem ikke at
, så kan du forenkle tilføjelsen af led til en multiplikation. Glem ikke at  kan betragtes som
kan betragtes som  , så det
, så det  ved at tilføje, hvor `1 af det + 1 af det = 2 af det`, uanset hvad `det` måtte være. Læg blot antallet af ens udtryk (dem med identisk grundtal og eksponent) sammen og multiplicer summen med det eksponentielle udtryk. Det kan du så
ved at tilføje, hvor `1 af det + 1 af det = 2 af det`, uanset hvad `det` måtte være. Læg blot antallet af ens udtryk (dem med identisk grundtal og eksponent) sammen og multiplicer summen med det eksponentielle udtryk. Det kan du så  løse og gange svaret med to. Husk, at dette er muligt, fordi en multiplikation ikke er andet end at omskrive en addition, fordi
løse og gange svaret med to. Husk, at dette er muligt, fordi en multiplikation ikke er andet end at omskrive en addition, fordi  . Her er et par eksempler:
. Her er et par eksempler: 
2. Multiplicer tal med samme grundtal ved at lægge eksponenterne sammen. Hvis du har to eksponenter med samme base, som f.eks  , så skal du blot tilføje de to eksponenter med samme base. Så,
, så skal du blot tilføje de to eksponenter med samme base. Så, . Hvis du synes, det er lidt mærkeligt, så opdel det i mindre dele for at forstå, hvordan systemet fungerer:
. Hvis du synes, det er lidt mærkeligt, så opdel det i mindre dele for at forstå, hvordan systemet fungerer:
 , så skal du blot tilføje de to eksponenter med samme base. Så,
, så skal du blot tilføje de to eksponenter med samme base. Så, . Hvis du synes, det er lidt mærkeligt, så opdel det i mindre dele for at forstå, hvordan systemet fungerer:
. Hvis du synes, det er lidt mærkeligt, så opdel det i mindre dele for at forstå, hvordan systemet fungerer:






3. Multiplicer et eksponentielt tal hævet til en anden potens, som f.eks ( x 2 ) 5  . Hvis du hæver et tal til en bestemt potens, og det hele hæves til en bestemt potens, skal du bare gange de to eksponenter. Så,
. Hvis du hæver et tal til en bestemt potens, og det hele hæves til en bestemt potens, skal du bare gange de to eksponenter. Så,  . Hvis du bliver forvirret, så tænk igen, hvad disse symboler egentlig betyder.
. Hvis du bliver forvirret, så tænk igen, hvad disse symboler egentlig betyder.  betyder bare dig
betyder bare dig  Multiplicerer 5 gange af sig selv, så:
Multiplicerer 5 gange af sig selv, så:
 . Hvis du hæver et tal til en bestemt potens, og det hele hæves til en bestemt potens, skal du bare gange de to eksponenter. Så,
. Hvis du hæver et tal til en bestemt potens, og det hele hæves til en bestemt potens, skal du bare gange de to eksponenter. Så,  . Hvis du bliver forvirret, så tænk igen, hvad disse symboler egentlig betyder.
. Hvis du bliver forvirret, så tænk igen, hvad disse symboler egentlig betyder.  betyder bare dig
betyder bare dig  Multiplicerer 5 gange af sig selv, så:
Multiplicerer 5 gange af sig selv, så:



4. Tænk på negative eksponenter som brøker eller det gensidige af tallet. Ved ikke hvad en gensidighed er, intet problem. Hvis du har at gøre med en negativ eksponent, som f.eks  , Gør derefter eksponenten positiv og placer denne som nævneren under én, hvilket resulterer i
, Gør derefter eksponenten positiv og placer denne som nævneren under én, hvilket resulterer i  . Her er et par ekstra eksempler:
. Her er et par ekstra eksempler:
 , Gør derefter eksponenten positiv og placer denne som nævneren under én, hvilket resulterer i
, Gør derefter eksponenten positiv og placer denne som nævneren under én, hvilket resulterer i  . Her er et par ekstra eksempler:
. Her er et par ekstra eksempler:


5. Divider to tal med samme grundtal ved at trække eksponenterne fra. Division er det modsatte af multiplikation, og selvom de ikke løses nøjagtigt som modsætninger, er de her. Hvis du har med ligningen at gøre  , Træk blot den øverste eksponent fra den nederste, og lad basen være som den er. Så,
, Træk blot den øverste eksponent fra den nederste, og lad basen være som den er. Så,  , eller 16.
, eller 16.
 , Træk blot den øverste eksponent fra den nederste, og lad basen være som den er. Så,
, Træk blot den øverste eksponent fra den nederste, og lad basen være som den er. Så,  , eller 16.
, eller 16. , omskrives som
, omskrives som  . Negative eksponenter danner brøker.
. Negative eksponenter danner brøker.
6. Prøv nogle øvelser for at vænne dig til at arbejde med potenstal. De følgende øvelser øver alt, der er diskuteret indtil videre. For svaret skal du blot vælge den linje, der indeholder problemet.
 = 125
= 125 = 12
= 12 = -x^12
= -x^12 =
=  Husk, at et tal uden potens har en eksponent på 1
Husk, at et tal uden potens har en eksponent på 1 =
= 
 =
= 
Metode 3 af 3: Løsning af brøker som potenstal

1. Behandl brøker i form af potenstal, som f.eks x 1 2  som en kvadratrod.
som en kvadratrod.  er faktisk nøjagtig det samme som
er faktisk nøjagtig det samme som  . Dette gælder uanset brøkens nævner, så
. Dette gælder uanset brøkens nævner, så  bliver andengradsroden af x, også skrevet som
bliver andengradsroden af x, også skrevet som ![Løsning af eksponenter {sqrt[ {4}]{x}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6193130540098748b8aecf0b95bf490c2ae3d867) .
.
 som en kvadratrod.
som en kvadratrod.  er faktisk nøjagtig det samme som
er faktisk nøjagtig det samme som  . Dette gælder uanset brøkens nævner, så
. Dette gælder uanset brøkens nævner, så  bliver andengradsroden af x, også skrevet som
bliver andengradsroden af x, også skrevet som ![Løsning af eksponenter {sqrt[ {4}]{x}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6193130540098748b8aecf0b95bf490c2ae3d867) .
. - Rødder er det omvendte af eksponenter. For eksempel hvis du tager svaret på
til fjerde potens, så kommer du tilbage til
, og det kan også
også skrives som
. Et andet eksempel er
og så
og dermed
.

2. Gør tælleren til en normaleksponent for en blandet brøk. kan se umuligt ud, men er let, hvis du husker, hvordan eksponenter ganges. Gør basen til en kvadratrod, som en normal brøk, og hæv det hele til potensen i toppen af brøken. Hvis du har svært ved at huske dette, så gennemgå teorien igen. Det gælder i sidste ende
kan se umuligt ud, men er let, hvis du husker, hvordan eksponenter ganges. Gør basen til en kvadratrod, som en normal brøk, og hæv det hele til potensen i toppen af brøken. Hvis du har svært ved at huske dette, så gennemgå teorien igen. Det gælder i sidste ende  bare lig
bare lig  For eksempel:
For eksempel:
 kan se umuligt ud, men er let, hvis du husker, hvordan eksponenter ganges. Gør basen til en kvadratrod, som en normal brøk, og hæv det hele til potensen i toppen af brøken. Hvis du har svært ved at huske dette, så gennemgå teorien igen. Det gælder i sidste ende
kan se umuligt ud, men er let, hvis du husker, hvordan eksponenter ganges. Gør basen til en kvadratrod, som en normal brøk, og hæv det hele til potensen i toppen af brøken. Hvis du har svært ved at huske dette, så gennemgå teorien igen. Det gælder i sidste ende  bare lig
bare lig  For eksempel:
For eksempel:

![Løsning af eksponenter x^{{{frac{1}{3}}}}={sqrt[ {3}]{x}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/759eade6ce89e27b301ccdcd83d7e8858827b8e2)
 =
= ![Løsning af eksponenter ({sqrt[ {3}]{x}})^{5}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8ea002d6365c3ba2d1d255162136605453a7135f)

3. Du kan addere, subtrahere og gange brøker i form af potenstal – præcis som du plejer. Det er meget nemmere at tilføje eller trække eksponenterne fra, før du løser eller konverterer dem til kvadratrødder. Hvis grundtallet er det samme, og eksponenten er den samme, så kan du bare tilføje og trække dem fra. Hvis kun grundtallet er det samme, så kan du gange og dividere eksponenterne som normalt, så længe du tager hensyn til hvordan man tilføjer og trækker brøker. For eksempel:


Tips
- De fleste lommeregnere har en knap til eksponenter - tryk efter indtastning af basen - til at løse problemer med potenstal.Normalt ligner dette en ^ eller x^y.
- `Forenkle` betyder i matematik udføre de nødvendige redigeringer for at få den enkleste form af de pågældende udtryk.
- 1 er eksponenternes identitetselement. Det betyder, at ethvert reelt tal hævet til 1 potens (til første potens) er selve tallet, for eksempel:
Også 1 er identitetselementet for multiplikation (1 som multiplikator, som f.eks
), og fra division (1 som udbytte, som f.eks
.
- Grundtallet nul til nul (0) er udefineret (engelsk: dne, eksisterer ikke). Computere eller regnemaskiner vil derefter returnere en `fejl`. Husk, at ethvert ikke-nul tal hævet til 0-potensen altid er lig med 1,
- For eksempel er højere matematik for imaginære tal,
, hvorved
; e er en irrationel, kontinuerlig konstant lig med 2,71828..., og a er en vilkårlig konstant. Beviset kan findes i de fleste højere matematikbøger.
Advarsler
- En eksponentiel stigning får produktet til at stige hurtigere og hurtigere, så svaret kan forekomme forkert, når det er korrekt. (Tjek dette ved for eksempel at tegne en eksponentiel funktion.: 2, hvis x har en række forskellige værdier).
Artikler om emnet "Løsning af eksponenter"
Оцените, пожалуйста статью
Populær