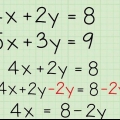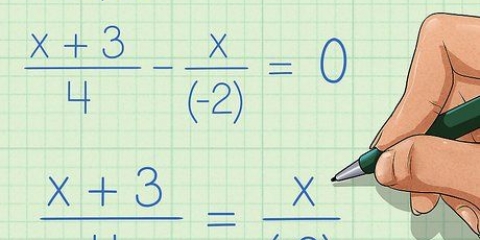2x - 2x = 0 4y - 2y = 2y 8 - 2 = 6 2x + 4y = 8-(2x + 2y = 2)=0 +2y = 6 
2y = 6 Divider 2y og 6 med 2 og få y = 3 
Indsæt y = 3 i ligningen 2x + 2y = 2 og løs for x. 2x + 2(3) = 2 2x + 6 = 2 2x = -4 x = - 2 Du har løst ligningssystemet ved subtraktion. (x, y) = (-2, 3) 
Udfyld (-2, 3) for (x, y) i ligningen 2x + 4y = 8. 2(-2) + 4(3) = 8 -4 + 12 = 8 8 = 8 Udfyld (-2, 3) for (x, y) i ligningen 2x + 2y = 2. 2(-2) + 2(3) = 2 -4 + 6 = 2 2 = 2 

3x + x = 4x 6y + -6y = 0 8 + 4 = 12 Hvis du kombinerer dette får du et nyt produkt: 3x + 6y = 8 +(x - 6y = 4) = 4x + 0 = 12 
4x + 0 = 12 4x = 12 Divider 4x og 12 med 3 for at få x = 3 
Sæt x = 3 ind i ligningen x - 6y = 4 for at finde y. 3 - 6 år = 4 -6y = 1 Divider -6y og 1 med -6 for at få y = -1/6. Du har løst ligningssystemet med addition. (x, y) = (3, -1/6) 
Udfyld (3, -1/6) for (x, y) i ligningen 3x + 6y = 8. 3(3) + 6(-1/6) = 8 9 - 1 = 8 8 = 8 Udfyld (3, -1/6) for (x, y) i ligningen x - 6y = 4. 3 - (6 * -1/6) =4 3 - - 1 = 4 3 + 1 = 4 4 = 4 

2 (2x - y = 2) 4x - 2y = 4 
3x + 2y = 10 + 4x - 2y = 4 7x + 0 = 14 7x = 14 

x = 2 ---> 2x - y = 2 4 - y = 2 -y = -2 y = 2 Du har løst ligningssystemet ved hjælp af multiplikation. (x, y) = (2, 2) 
Udfyld (2, 2) for (x, y) i ligningen 3x + 2y = 10. 3(2) + 2(2) = 10 6 + 4 = 10 10 = 10 Udfyld (2, 2) for (x, y) i ligningen 2x - y = 2. 2(2) - 2 = 2 4 - 2 = 2 2 = 2 

x = 2 - 4y --> 2x + 3y = 9 2(2 - 4y) + 3y = 9 4 - 8 år + 3 år = 9 4 - 5 år = 9 -5 år = 9 - 4 -5 år = 5 -y = 1 y = - 1 
y = -1 --> x = 2 - 4y x = 2 - 4(-1) x = 2 - -4 x = 2 + 4 x = 6 Du løste ligningssystemet ved hjælp af substitution. (x, y) = (6, -1) 
Udfyld (6, -1) for (x, y) i ligningen 2x + 3y = 9. 2(6) + 3(-1) = 9 12 - 3 = 9 9 = 9 Udfyld (6, -1) for (x, y) i ligningen x + 4y = 2. 6 + 4(-1) = 2 6 - 4 = 2 2 = 2
Løsning af et ligningssystem
Indhold
At løse et ligningssystem kræver at finde værdien af flere variable i flere ligninger. Du kan løse et ligningssystem ved hjælp af addition, subtraktion, multiplikation eller substitution. Hvis du gerne vil lære at løse et ligningssystem, er alt hvad du skal gøre at følge disse trin.
Trin
Metode 1 af 4: Løs ved subtraktion

1. Skriv den ene ligning over den anden. At løse disse ligninger med subtraktion er en ideel metode, hvis du ser, at begge ligninger har den samme variabel med samme koefficient og fortegn. For eksempel, hvis begge ligninger har variablen -2x, kan du bruge subtraktion til at finde værdien af begge variabler.
- Skriv den ene ligning over den anden, så x- og y-variablerne i begge ligninger og tallene er under hinanden. Placer minustegnet ved siden af det nederste nummer.
- F.eks.: Hvis du har følgende to ligninger: 2x + 4y = 8 og 2x + 2y = 2, ville det se sådan ud:
- 2x + 4y = 8
- -(2x + 2y = 2)

2. Træk lignende udtryk fra. Nu hvor de to ligninger er justeret, skal du bare trække de lignende udtryk fra. Gør dette med et termin ad gangen:

3. Løs for den resterende periode. Fjern ethvert nul fra ligningen, der er blevet oprettet, det ændrer ikke værdien, og løs den resterende ligning.

4. Indtast den fundne værdi af variablen i en af ligningerne. Nu hvor du ved, at y = 3, kan du sætte denne værdi ind i den oprindelige ligning for at løse for x. Uanset hvilken ligning du vælger, er svaret det samme. Så brug den enkleste ligning!

5. Tjek dit svar. For at sikre, at dit svar er korrekt, skal du indtaste begge svar i begge ligninger. Sådan gør du det:
Metode 2 af 4: Løs ved tilføjelse

1. Skriv den ene ligning over den anden. At løse et ligningssystem ved addition er den bedste metode, hvis du bemærker, at begge ligninger har en variabel med samme koefficient, men med forskelligt fortegn; for eksempel, hvis den ene ligning indeholder variablen 3x og den anden variablen -3x.
- Skriv den ene ligning over den anden, så x- og y-variablerne i begge ligninger og tallene er under hinanden. Placer plustegnet ved siden af det nederste nummer.
- F.eks.: Du har følgende to ligninger 3x + 6y = 8 og x - 6y = 4, og skriv derefter den første ligning over den anden som vist nedenfor:
- 3x + 6y = 8
- +(x - 6y = 4)

2. Tilføj lignende udtryk sammen. Nu hvor de to ligninger er justeret over hinanden, er alt hvad du skal gøre at tilføje termerne med den samme variabel sammen:

3. Løs for den resterende periode. Fjern eventuelt nul fra ligningen, der er opstået, det ændrer ikke værdien. Løs den resterende ligning.

4. Indtast den fundne værdi af denne variabel i en af ligningerne. Nu hvor du ved, at x = 3, kan du sætte denne værdi ind i den oprindelige ligning for at løse for y. Uanset hvilken ligning du vælger, er svaret det samme. Så brug den enkleste ligning!

5. Tjek dit svar. For at sikre, at dit svar er korrekt, skal du indtaste begge svar i begge ligninger. Sådan gør du det:
Metode 3 af 4: Løs ved multiplikation

1. Skriv den ene ligning over den anden. Skriv den ene ligning over den anden, så x- og y-variablerne i begge ligninger og tallene er under hinanden. Hvis du bruger multiplikation, gør du det, fordi ingen af variablerne har ens koefficienter - lige nu.
- 3x + 2y = 10
- 2x - y = 2

2. Sørg for ens koefficienter. Gang derefter en eller begge ligninger med et tal, så en af variablerne har samme koefficient. I dette tilfælde kan du gange hele den anden ligning med 2, så -y er lig med -2y og dermed den første y-koefficient. Sådan gør du det:

3. Tilføj eller subtraher ligningerne. Nu skal du blot fjerne lige store vilkår ved at lægge til eller trække fra. Da du har at gøre med 2y og -2y her, giver det mening at bruge additionsmetoden, fordi den er lig med 0. Hvis du har at gøre med 2y + 2y, skal du bruge subtraktionsmetoden. Her er et eksempel på, hvordan man bruger additionsmetoden til at eliminere variabler:

4. Løs dette for den resterende periode. Dette løses nemt ved at finde værdien af det udtryk, som du endnu ikke har elimineret. Hvis 7x = 14, så er x = 2.

5. Indtast den fundne værdi i en af ligningerne. Indtast led i en af de oprindelige ligninger for at løse for det andet led. Vælg den enkleste ligning for dette, dette er den hurtigste.

6. Tjek dit svar. For at sikre, at dit svar er korrekt, skal du indtaste begge svar i begge ligninger. Sådan gør du det:
Metode 4 af 4: Løs ved substitution

1. Isoler en variabel. Substitution er ideel, når en af koefficienterne i en af ligningerne er lig med 1. Så er alt, du skal gøre, at isolere denne variabel til den ene side af ligningen for at finde dens værdi.
- Hvis du arbejder med ligningerne 2x + 3y = 9 og x + 4y = 2, så skal du isolere x i den anden ligning.
- x + 4y = 2
- x = 2 - 4y

2. Udfyld værdien af den variabel, du isolerede i den anden ligning. Tag værdien af den isolerede variabel og sæt den ind i den anden ligning. Selvfølgelig ikke i samme ligning ellers løser du ikke noget. Her er et eksempel på, hvordan man gør det:

3. Løs for den resterende variabel. Nu hvor du ved, at y = - 1, sæt denne værdi ind i den enklere ligning for at finde værdien af x. Her er et eksempel på, hvordan du gør det:

4. Tjek dit svar. For at sikre, at dit svar er korrekt, skal du indtaste begge svar i begge ligninger. Sådan gør du det:
Tips
- Du burde nu være i stand til at løse ethvert lineært ligningssystem ved hjælp af addition, subtraktion, multiplikation eller substitution, men én metode er normalt den mest egnede afhængigt af ligningerne.
Artikler om emnet "Løsning af et ligningssystem"
Оцените, пожалуйста статью
Populær