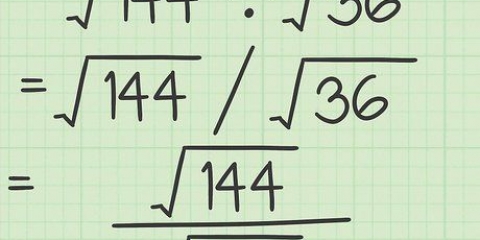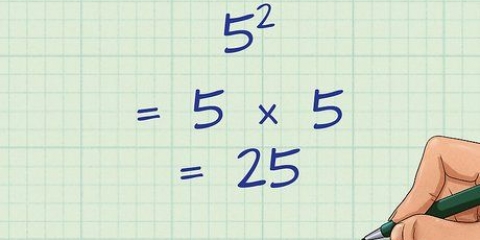For eksempel: brøken  kan du forenkle til
kan du forenkle til  . Så,
. Så, 

For eksempel: fordi  , kan du omskrive det eksponentielle udtryk som
, kan du omskrive det eksponentielle udtryk som  .
. 
For eksempel:  .
. 
For eksempel: fordi ![Løsning af decimaleksponenter 81^{{{frac{1}{4}}}}={sqrt[ {4}]{81}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b37415d73d383d0450962dda1cf0ddb2e0da0452) , kan du omskrive ligningen som
, kan du omskrive ligningen som ![Løsning af decimaleksponenter ({sqrt[ {4}]{81}})^{{3}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/79a4e12743be369be81296fe2aeabd97c70cb9ab) .
. 
For eksempel: Om ![Løsning af decimaleksponenter {sqrt[ {4}]{81}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/44f5722ccf46fec0200534e84bda483bc2b726b1) for at beregne, skal du bestemme, hvilket tal ganget med fire er lig med 81. Fordi
for at beregne, skal du bestemme, hvilket tal ganget med fire er lig med 81. Fordi  , ved du
, ved du ![Løsning af decimaleksponenter {sqrt[ {4}]{81}}=3](https://wikimedia.org/api/rest_v1/media/math/render/svg/44d91764f62522cec7024ef6481f0b83305f17e9) . Så eksponentialligningen bliver nu
. Så eksponentialligningen bliver nu  .
. 
For eksempel:  . Så,
. Så,  .
. 

Decimalen  er lig med
er lig med  , Så
, Så  .
. 
Fordi  er forenklet til
er forenklet til  , tæller det
, tæller det  .
. Hvis du konverterer dette til en uægte brøk, får du  . Så,
. Så,  .
. 






For eksempel:  .
. 
For eksempel:  .
. 
![Løsning af decimaleksponenter x^{{{frac{1}{3}}}}={sqrt[ {3}]{x}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/759eade6ce89e27b301ccdcd83d7e8858827b8e2)
![Løsning af decimaleksponenter x^{{{frac{1}{4}}}}={sqrt[ {4}]{x}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/625ea5fe7631555b2fc23ac21f595d7c20633ec9)
![Løsning af decimaleksponenter x^{{{frac{1}{5}}}}={sqrt[ {5}]{x}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/788c8c448ea3cf9b81867b10ba6bbb1a47abb388)
For eksempel: ![Løsning af decimaleksponenter 81^{{{frac{1}{4}}}}={sqrt[ {4}]{81}}=3](https://wikimedia.org/api/rest_v1/media/math/render/svg/0af496f05893da79ec2c45b4ebebabce0930dce0) . Du ved, at tre er den fjerde rod af 81, fordi
. Du ved, at tre er den fjerde rod af 81, fordi 

Hvis du har at gøre med kvadratrodseksponenter, så bliver denne lov  , fordi
, fordi  .
.
Løsning af decimaleksponenter
Indhold
Beregning af eksponenter er en grundlæggende færdighed, som eleverne lærer i præ-algebra. Normalt ser man eksponenter som hele tal, og nogle gange ser man dem som brøker. Sjældent ser du dem som decimaler. Når en eksponent vises som en decimal, skal du konvertere decimalen til en brøk. Dernæst er der nogle regler og love vedrørende eksponenter, som du kan bruge til at beregne udtrykket.
Trin
Del 1 af 3: Beregning af en decimaleksponent

1. Konverter decimalen til en brøk. For at konvertere en decimal til en brøk, skal du overveje pladsværdien. Brøkens nævner er pladsværdien. Decimaltegnets cifre er lig med tælleren.
- For eksempel: for det eksponentielle udtryk
, skal du
konvertere til en brøk. Da decimalen går til hundrededele pladsen, er den tilsvarende brøk
.

2. Forenkle brøken, hvis det er muligt. Da du tager en rod, der svarer til nævneren af brøkdelen af eksponenten, vil du have, at nævneren skal være så lille som muligt. Gør dette forenkling af pausen. Hvis brøken er et blandet tal (d.w.z. hvis din eksponent er en decimal større end 1), omskriv den som en uægte brøk.
 kan du forenkle til
kan du forenkle til  . Så,
. Så, 

3. Omskriv eksponenten som en multiplikation. Det gør du ved at gøre tælleren til et heltal og gange det med stambrøken. Rodbrøken er brøken med samme nævner, men med 1 som tæller.
 , kan du omskrive det eksponentielle udtryk som
, kan du omskrive det eksponentielle udtryk som  .
.
4. Omskriv eksponenten som en potens af en potens. Husk at gange med to eksponenter er det samme som potensen af en potens. Så  bliver til
bliver til  .
.
 bliver til
bliver til  .
. .
.
5. Omskriv basen som en kvadratrodsligning. At beregne eksponenten af et tal svarer til at beregne en passende rod af dette tal. Så omskriv grundtallet og den første eksponent som en kvadratrodsligning.
![Løsning af decimaleksponenter 81^{{{frac{1}{4}}}}={sqrt[ {4}]{81}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b37415d73d383d0450962dda1cf0ddb2e0da0452) , kan du omskrive ligningen som
, kan du omskrive ligningen som ![Løsning af decimaleksponenter ({sqrt[ {4}]{81}})^{{3}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/79a4e12743be369be81296fe2aeabd97c70cb9ab) .
.
6. Beregn kvadratrodsligningen. Husk, at rodeksponenten (det lille tal uden for radikalen) fortæller dig, hvilken rod du leder efter. Hvis tallene er vanskelige, er det bedst at gøre dette med ![Løsning af decimaleksponenter {sqrt[ {x}]{y}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/58c28156258e3c4cf15e8af14abcc0163150e3e6) funktion på en matematikberegner.
funktion på en matematikberegner.
![Løsning af decimaleksponenter {sqrt[ {x}]{y}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/58c28156258e3c4cf15e8af14abcc0163150e3e6) funktion på en matematikberegner.
funktion på en matematikberegner.![Løsning af decimaleksponenter {sqrt[ {4}]{81}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/44f5722ccf46fec0200534e84bda483bc2b726b1) for at beregne, skal du bestemme, hvilket tal ganget med fire er lig med 81. Fordi
for at beregne, skal du bestemme, hvilket tal ganget med fire er lig med 81. Fordi  , ved du
, ved du ![Løsning af decimaleksponenter {sqrt[ {4}]{81}}=3](https://wikimedia.org/api/rest_v1/media/math/render/svg/44d91764f62522cec7024ef6481f0b83305f17e9) . Så eksponentialligningen bliver nu
. Så eksponentialligningen bliver nu  .
.
7. Beregn den resterende eksponent. Du skal nu have et helt tal som eksponent, så regnestykket skulle ellers være simpelt. Du kan altid bruge en lommeregner, hvis tallene er for store.
 . Så,
. Så,  .
.Del 2 af 3: Løsning af et eksempelproblem

1. Beregn følgende eksponentialligning: .
.
 .
.
2. Konverter decimalen til en brøk. Fordi  er større end 1, er brøken et blandet tal.
er større end 1, er brøken et blandet tal.
 er større end 1, er brøken et blandet tal.
er større end 1, er brøken et blandet tal. er lig med
er lig med  , Så
, Så  .
.
3. Forenkle brøken, hvis det er muligt. Du skal også konvertere ethvert blandet tal til uægte brøker.
 er forenklet til
er forenklet til  , tæller det
, tæller det  .
. . Så,
. Så,  .
.
4. Omskriv eksponenten som en multiplikation. Fordi  , kan du omskrive ligningen som
, kan du omskrive ligningen som  .
.
 , kan du omskrive ligningen som
, kan du omskrive ligningen som  .
.
5. Omskriv eksponenten som en potens af en potens. Så,  .
.
 .
.
6. Omskriv basen som en kvadratrodsligning.![Løsning af decimaleksponenter 256^{{{frac{1}{4}}}}={sqrt[ {4}]{256}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cb9c02c237d2aeb16bc1fd12eaf89cbde1d683a4) , som giver dig mulighed for at omskrive ligningen som
, som giver dig mulighed for at omskrive ligningen som ![Løsning af decimaleksponenter ({sqrt[ {4}]{256}})^{{9}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/261990049bf6155622a73330e280af3d17084588) .
.
![Løsning af decimaleksponenter 256^{{{frac{1}{4}}}}={sqrt[ {4}]{256}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cb9c02c237d2aeb16bc1fd12eaf89cbde1d683a4) , som giver dig mulighed for at omskrive ligningen som
, som giver dig mulighed for at omskrive ligningen som ![Løsning af decimaleksponenter ({sqrt[ {4}]{256}})^{{9}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/261990049bf6155622a73330e280af3d17084588) .
.
7. Beregn kvadratrodsligningen.![Løsning af decimaleksponenter {sqrt[ {4}]{256}}=4](https://wikimedia.org/api/rest_v1/media/math/render/svg/55bb3e8f3f86ce5c35d5f18ddd8f486e75e67476) . Så ligningen er nu
. Så ligningen er nu  .
.
![Løsning af decimaleksponenter {sqrt[ {4}]{256}}=4](https://wikimedia.org/api/rest_v1/media/math/render/svg/55bb3e8f3f86ce5c35d5f18ddd8f486e75e67476) . Så ligningen er nu
. Så ligningen er nu  .
.
8. Beregn den resterende eksponent. . Så,
. Så,  .
.
 . Så,
. Så,  .
.Del 3 af 3: Forståelse af eksponenter

1. Genkend en eksponentiel ligning. En eksponentiel ligning har en base og en eksponent. Grundlaget er det største tal i ligningen. Eksponenten er det mindste tal.
- For eksempel: i ligningen
, er
basen og
eksponenten.

2. Genkend delene af en eksponentialligning. Grundlaget er det tal, der ganges. Eksponenten angiver, hvor ofte basen bruges som faktor i ligningen.
 .
.
3. Genkend en kvadratrodseksponent. En kvadratrodseksponent kan også kaldes en brøkeksponent. Det er en eksponent i form af en brøk.
 .
.
4. Forstå sammenhængen mellem kvadratrods- og kvadratrodseksponenter. Ophøjelsen  af et tal er som kvadratroden af det tal. Så,
af et tal er som kvadratroden af det tal. Så,  . Det samme gælder for andre rødder og eksponenter. Nævneren af eksponenten fortæller dig, hvilken rod du skal tage:
. Det samme gælder for andre rødder og eksponenter. Nævneren af eksponenten fortæller dig, hvilken rod du skal tage:
 af et tal er som kvadratroden af det tal. Så,
af et tal er som kvadratroden af det tal. Så,  . Det samme gælder for andre rødder og eksponenter. Nævneren af eksponenten fortæller dig, hvilken rod du skal tage:
. Det samme gælder for andre rødder og eksponenter. Nævneren af eksponenten fortæller dig, hvilken rod du skal tage:![Løsning af decimaleksponenter x^{{{frac{1}{3}}}}={sqrt[ {3}]{x}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/759eade6ce89e27b301ccdcd83d7e8858827b8e2)
![Løsning af decimaleksponenter x^{{{frac{1}{4}}}}={sqrt[ {4}]{x}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/625ea5fe7631555b2fc23ac21f595d7c20633ec9)
![Løsning af decimaleksponenter x^{{{frac{1}{5}}}}={sqrt[ {5}]{x}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/788c8c448ea3cf9b81867b10ba6bbb1a47abb388)
![Løsning af decimaleksponenter 81^{{{frac{1}{4}}}}={sqrt[ {4}]{81}}=3](https://wikimedia.org/api/rest_v1/media/math/render/svg/0af496f05893da79ec2c45b4ebebabce0930dce0) . Du ved, at tre er den fjerde rod af 81, fordi
. Du ved, at tre er den fjerde rod af 81, fordi 

5. Forstå en magts eksponentielle lov om magt. Denne lov siger det  . Med andre ord, at hæve en eksponent til potens er det samme som at gange to eksponenter.
. Med andre ord, at hæve en eksponent til potens er det samme som at gange to eksponenter.
 . Med andre ord, at hæve en eksponent til potens er det samme som at gange to eksponenter.
. Med andre ord, at hæve en eksponent til potens er det samme som at gange to eksponenter. , fordi
, fordi  .
.Artikler om emnet "Løsning af decimaleksponenter"
Оцените, пожалуйста статью
Populær