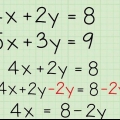Løsning af en kubikligning

Indhold

Trin

Første gang du støder på en kubisk ligning (af formen økse + bx + cx + d=0) det kan se næsten uløseligt ud. Imidlertid har denne metode til at løse kubiske ligninger eksisteret i århundreder! Det blev opdaget i det 16. århundrede af de italienske matematikere Niccolò Tartaglia og Gerolamo Cardano. Det var en af de første formler, der var ukendte for de gamle grækere og romere. At løse kubiske ligninger kan være meget vanskeligt, men med den rigtige tilgang (og nok grundlæggende viden) kan selv de vanskeligste kubiske ligninger tæmmes.

Trin

Metode 1 af 3: Løsning med abc-formlen

1. Tjek om kubikligningen indeholder en konstant. Som angivet ovenfor har kubiske ligninger formen økse + bx + cx + d=0. b, c, og d kan være 0 uden at ændre på, om det er en kubisk ligning eller ej - hvilket i bund og grund betyder, at en ligning ikke behøver at bestå af alle led bx, cx eller d at være en kubikligning. Du begynder at anvende denne relativt simple metode til at løse kubiske ligninger ved først at kontrollere, om din ligning har en konstant (en d-hvor er). Er det ikke tilfældet, så kan du de abc formel at finde svarene på ligningen med lidt matematik.

Hvis ligningen indeholder en konstant, bliver du nødt til at bruge en anden metode. Se nedenfor for alternative tilgange.

Billede med titlen Løs en kubisk ligning Trin 2

2. opløse en x ud af ligningen. Da din ligning ikke indeholder en konstant, har hvert led i ligningen en x-variabel. Det betyder, at en x kan tages ud af ligningen for at forenkle den. Gør dette og omskriv din ligning i formularen x(økse + bx + c).

Antag for eksempel, at du har ligningen 3x + -2x + 14x=0. Ved en x udenfor parentes, får vi x(3x + -2x + 14)=0.

Billede med titlen Løs en kubisk ligning Trin 3

3. Brug abc-formlen til at løse begreberne i parentes. Du har måske bemærket, at vilkårene for din nye ligning i parentes er i form af en andengradsligning (økse + bx + c). Det betyder, at vi kan finde de værdier, for hvilke andengradsligningen er lig med nul a, b og c i abc-formlen ({-b +/-√ (b- 4ac)}/2-en). Dette vil finde to af svarene på din kubiske ligning.

I vores eksempeludsagn udfylder vi vores værdier a, b og c (henholdsvis 3, -2 og 14) i andengradsligningen i:

{-b +/-√ (b- 4ac)}/2-en

{-(-2) +/-√ ((-2)-4(3)(14))}/2(3)

{2 +/-√ (4 - (12)(14))}/6

{2 +/-√ (4 - (168)}/6

{2 +/-√ (-164)}/6

Svar 1:

{2 + √(-164)}/6

{2 + 12.8jeg}/6

Svar 2:

{2-12.8jeg}/6

Billede med titlen Løs en kubisk ligning Trin 4

4. Brug nul og kvadratiske svar som svar på din kubikligning. Firkantede ligninger har to løsninger, men kubiske ligninger har tre. Du har allerede to - det er svarene, du fandt ved at regne ud den "kvadratlige ligning" i parentes. I de tilfælde, hvor en ligning er passende for denne `uden for parentes`, vil det tredje svar altid være 0 er. Tillykke - du har lige løst en kubikligning.

Grunden til, at dette virker, har at gøre med det grundlæggende faktum, at ethvert tal ganget med nul er lig med nul. Når du konverterer ligningen til formen x(økse + bx + c)=0, du opdeler i det væsentlige de to i dele: den ene del er x-variabel uden for parentes, og den anden er kvadratet inde i parentes. Hvis nogen af disse dele er lig med nul, så er hele ligningen det også. Så hvis de to svar på kvadratet inde i parentesen gør den del til nul, så vil svarene på den kubiske ligning også gøre delen uden for parentesen lig med nul.

Metode 2 af 3: Løsning ved hjælp af faktorlister

Billede med titlen Løs en kubisk ligning Trin 5

1. Sørg for, at din kubiske ligning har en konstant. Selvom ovenstående metode er nyttig, fordi den ikke kræver, at du lærer nye matematiske færdigheder, vil den ikke altid fungere til at løse kubiske ligninger. Hvis din ligning er i formen økse + bx + cx + d=0 tilstand, og d er ikke-nul, vil parenteserne ikke virke, og du skal bruge enten denne metode eller den i næste del.

Antag for eksempel, at du har den givne ligning 2x + 9x + 13x=-6. I dette tilfælde vil et 0 til højre for lighedstegnet kræve tilføjelse af 6 til begge sider. Vores nye ligning er 2x + 9x + 13x + 6=0, d=6, så vi kan ikke bruge parenteserne fra forrige del.

Billede med titlen Løs en kubisk ligning Trin 6

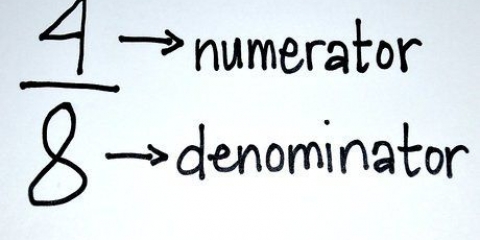
2. Bestem faktorerne ved -en og d. For at løse den kubiske ligning, start med at bestemme faktorerne for -en (koefficienten af x vilkår d (konstanten i slutningen af ligningen). Som en påmindelse er faktorer de tal, der ganges sammen danner et andet tal. For eksempel fordi din 6 opstår fra multiplikationen 6 &tid; 1 og 2 × 3, er 1, 2, 3 og 6 faktorer af 6.

I vores eksempeludsagn, -en=2 og d=6. Faktorerne på 2 er 1 og 2. Faktorerne på 6 er 1, 2, 3 og 6.

Billede med titlen Løs en kubisk ligning Trin 7

3. Del faktorerne ved -en af faktorerne d. Nu lister du alle de værdier, du får ved at dividere hver faktor -en af enhver faktor d. Dette resulterer normalt i mange brøker og nogle få heltal. Heltalsløsningerne af din kubiske ligning vil enten være et af heltalene fra listen eller det negative tal af et af disse tal.

I vores ligning beregner du faktorerne af -en (1, 2) om faktorerne vedr d (1, 2, 3, 6) og du får følgende liste: 1, 1/2, 1/3, 1/6, 2 og 2/3. Nu tilføjer vi de negative tal til listen for at gøre den komplet: 1, -1, 1/2, -1/2, 1/3, -1/3, 1/6, -1/6, 2, -2, 2/3 og -2/3. Heltalsløsningen af vores kubiske ligning kan findes et sted på denne liste.

Billede med titlen Løs en kubisk ligning Trin 8

4. Brug syntetisk deling til manuelt at kontrollere dine svar. Når du har kompileret listen over værdier, kan du finde heltalsløsningerne til din kubikligning ved hurtigt manuelt at indtaste hvert heltal og kontrollere, hvilke der er lig med nul. Hvis du ikke vil bruge tid på dette, er der en lidt hurtigere metode iflg en teknik kaldet syntetisk deling. Essensen er, at du dividerer heltal med originalen a, b, c og d koefficienter for din kubiske ligning. Hvis du står tilbage med en rest på 0, er din værdi en af løsningerne af den kubiske ligning.

Syntetisk deling er et komplekst emne - følg linket ovenfor for at få flere oplysninger. Her er et eksempel på at finde en af løsningerne til vores kubiske ligning ved hjælp af syntetisk division:

-1 | 2 9 13 6

__| -2-7-6

__| 2 7 6 0

Da vi ender med 0 som rest, ved vi, at en af løsningerne på vores kubiske ligning er heltal -1 er.

Metode 3 af 3: Brug af `diskriminerende`

Billede med titlen Løs en kubisk ligning Trin 9

1. Skriv værdierne af a, b, c og d. I denne metode til at finde løsningerne af en kubisk ligning, vil vi i høj grad stole på koefficienterne for led i vores ligning. Af denne grund er det klogt at bruge vilkårene a, b, c og d skriv det ned, før du starter, så du ikke glemmer, hvad hver enkelt er.

For eksempel til sammenligningen x - 3x + 3x - 1, skriver vi -en=1, b=-3, c=3 og d=-1. Glem ikke det af en x-variabel uden koefficient antages det, at koefficienten er lig med 1.

Billede med titlen Løs en kubisk ligning Trin 10

2. Beregn Δ0=b - 3ac. Når du bruger diskriminanten til at løse kubiske ligninger, har du brug for lidt mere avanceret matematik, men hvis du følger proceduren omhyggeligt, vil du opleve, at den er et værdifuldt værktøj til at løse de i forvejen vanskelige kubiske ligninger. Start med at finde Δ0, den første af flere vigtige værdier, vi har brug for, ved at erstatte de passende værdier i formlen b - 3ac.

I vores eksempelopgave løser vi dette som følger:

b - 3ac

(-3) - 3(1)(3)

9 - 3(1)(3)

9 - 9=0=Δ0

Billede med titlen Løs en kubisk ligning Trin 11

3. Beregn Δ1=2b - 9ABC + 27-end. Den næste vigtige mængde, vi har brug for, Δ1, kræver lidt mere arbejde, men kan findes på nogenlunde samme måde som Δ0. Erstat de korrekte værdier i formlen 2b - 9ABC + 27-end for værdien af Δ1.

I vores eksempelopgave løser vi dette som følger:

2(-3) - 9(1)(-3)(3) + 27(1)(-1)

2(-27) - 9(-9) + 27(-1)

-54 + 81 - 27

81 - 81=0=Δ1

Billede med titlen Løs en kubisk ligning Trin 12

4. Beregn Δ=Δ1 - 4Δ0) ÷ -27-en. Så beregner vi diskriminerende af den kubiske ligning fra værdierne for Δ0 og Δ1. En diskriminant er simpelthen et tal, der fortæller os noget om svarene på et polynomium (ubevidst kender du måske allerede den kvadratiske diskriminant: b - 4ac). I tilfælde af den kubiske ligning, hvis diskriminanten er positiv, så har ligningen tre reelle løsninger. Hvis diskriminanten er nul, så har ligningen en eller to reelle løsninger, og nogle af disse løsninger er fælles. Hvis den er negativ, har ligningen kun én løsning. (En kubisk ligning har altid én reel løsning, fordi grafen altid er mindst én gang med x-akseskæringer.)

I vores eksempelopgave er det meget simpelt at bestemme Δ, fordi både Δ0 og Δ1=0. Vi løser dette på følgende måde:

Δ1 - 4Δ0) ÷ -27-en

(0) - 4(0)) -27(1)

0 - 0 27

0=Δ, så vores ligning har 1 eller 2 svar.

Billede med titlen Løs en kubisk ligning Trin 13

5. Beregn C=√(√((Δ1 - 4Δ0) + Δ1)/ 2). Den sidste vigtige værdi at beregne er C. Med denne vigtige mængde kan vi endelig finde de tre løsninger. Løs dette som sædvanligt, udskift Δ1 og Δ0, hvor det er nødvendigt.

I vores eksempelproblem finder vi C som følger:

√(√((Δ1 - 4Δ0) + Δ1)/ 2)

√(√((0 - 4(0)) + (0))/ 2)

√(√((0 - 0) + (0))/ 2)

0=C

Billede med titlen Løs en kubisk ligning Trin 14

6. Beregn de tre svar med dine variable. Svarene på din kubikligning er givet af formlen (b + uC + (Δ0/uC)) / 3-en, hvorved du=(-1 + √(-3))/2 og n er 1, 2 eller 3. Indtast dine værdier, hvor det er nødvendigt for at løse dette - dette kræver en masse matematik, men bør give dig tre mulige svar!

I vores eksempelopgave kan vi løse dette ved at kontrollere svaret, når n er lig med 1, 2 eller 3. Svarene vi får fra disse test er de mulige svar på vores kubiske ligning - enhver løsning, der giver 0 efter substitution i ligningen er korrekt. Antag for eksempel, at vi får 1 som svar på en af testene, fordi at indtaste 1 i x - 3x + 3x - 1 resulterer i 0 hvis svaret, så 1 et af svarene på vores kubikligning.