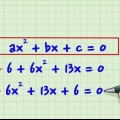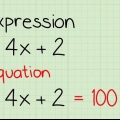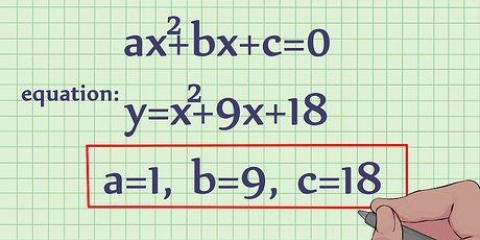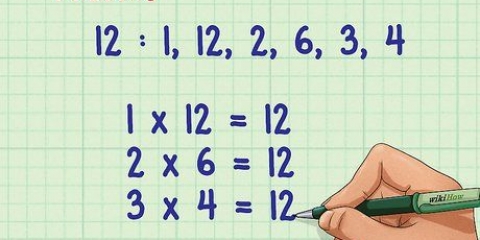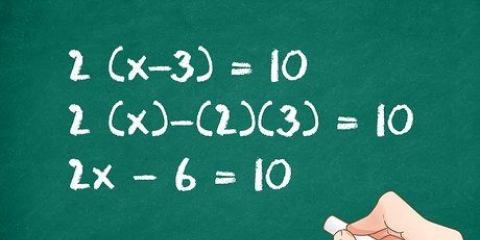Da 3x har et begrænset antal mulige faktorer, 3x og x, kan du skrive disse i parentes: (3x +/- ? )(x +/-- ?) = 0. Brug derefter en elimineringsmetode, hvor du bruger faktorerne 4 til at finde en kombination, der giver -11x som resultat af multiplikationen. Du kan bruge enten en kombination af 4 og 1 eller 2 og 2, fordi multiplikationen af begge talkombinationer giver 4. Husk, at en af termerne skal være negativ, fordi termen er -4. Prøv (3x +1)(x -4). Når du regner dette ud får du - 3x -12x +x -4. Kombinerer du vilkårene -12x og x får du -11x, som er den mellemste termin du ønskede at komme frem til. Nu har du indregnet denne andengradsligning. Et andet eksempel; vi forsøger at faktorisere en ligning, der ikke virker: (3x-2)(x+2) = 3x +6x -2x -4. Hvis du kombinerer disse udtryk, får du 3x -4x -4. Selvom produktet af -2 og 2 er lig med -4, virker mellemleddet ikke, fordi du ledte efter -11x, ikke -4x. 

3x + 1 = 0 = 3x = -1 = 3x/3 = -1/3 x = -1/3 x - 4 = 0 x = 4 x = (-1/3, 4) 

Så begge løsninger fungerer hver for sig, og begge er verificeret som fungerende og er korrekte i to forskellige løsninger. 



{-b +/-√ (b - 4ac)}/2 {-(-5) +/-√ ((-5) - 4(3)(-8))}/2(3) = {-(-5) +/-√ ((-5) - (-96))}/2(3) 
{-(-5) +/-√ ((-5) - (-96))}/2(3) = {5 +/-√(25 + 96)}/6 {5 +/-√(121)}/6 

(5 + 11)/6 (5 - 11)/6 
(5 + 11)/6 = 16/6 (5-11)/6 = -6/6 
16/6 = 8/3 -6/6 = -1 x = (-1, 8/3) 

2x - 12x - 9 = 0 2x - 12x = 9 
2x/2 - 12x/2 = 9/2 = x - 6x = 9/2 
-6/2 = -3 = (-3) = 9 = x - 6x + 9 = 9/2 + 9 


x = 3 +(√6)/2 x = 3 - (√6)/2)
Løs andengradsligninger
Indhold
En andengradsligning er en ligning, hvor den største eksponent for en variabel er to. Tre af de mest almindeligt anvendte metoder til at løse disse ligninger er: faktorisering, brug af abc-formlen eller dividering af kvadratet. Hvis du vil vide, hvordan du mestrer disse metoder, skal du blot følge disse trin.
Trin
Metode 1 af 3: Factoring

1. Flyt alle led til den ene side af ligningen. Det første trin i factoring er at flytte alle led til den ene side af ligningen, hvilket efterlader x positiv. Anvend additions- eller subtraktionsoperationen på vilkårene x, variablen x og konstanterne, flyt dem til den ene side af ligningen på denne måde, uden at efterlade noget på den anden side. Sådan fungerer det:
- 2x - 8x - 4 = 3x - x =
- 2x +x - 8x -3x - 4 = 0
- 3x - 11x = 0

2. Faktor udtrykket. For at faktorisere udtrykket skal du faktorisere faktorerne 3x og faktorerne af konstanten -4 for at gange dem og derefter lægge dem sammen for at give værdien af mellemleddet, -11. Sådan gør du det:

3. Bestem, at hvert par parenteser er lig med nul og behandle dem som separate ligninger. Dette får dig til at finde to værdier for x, der begge gør hele ligningen lig med nul. Nu hvor du har indregnet ligningen, er der kun tilbage at gøre hvert par parentes lig med nul. Så du kan skrive at: 3x +1 = 0 og x - 4 = 0.

4. Løs hver ligning. I en andengradsligning er der to givne værdier for x. Løs hver ligning separat ved at isolere variablen og skriv resultaterne af x. Sådan går det:

5. Tjek x = -1/3 in (3x + 1)(x – 4) = 0:
Vi får (3[-1/3] + 1)([-1/3] – 4) ?=? 0 ..... ved at erstatte:(-1 + 1)(-4 1/3) ?=? 0 ..... ved at forenkle:(0)(-4 1/3) = 0 ..... ved at gange: så 0=0 ..... Ja, x = -1/3 virker
Vi får (3[-1/3] + 1)([-1/3] – 4) ?=? 0 ..... ved at erstatte:(-1 + 1)(-4 1/3) ?=? 0 ..... ved at forenkle:(0)(-4 1/3) = 0 ..... ved at gange: så 0=0 ..... Ja, x = -1/3 virker

6. Tjek x = 4 tommer (3x + 1)(x - 4) = 0:
Vi får (3[4] + 1)([4] – 4) ?=? 0..... ved at erstatte:(13)(4 – 4) ?=? 0 ..... ved at dæmpe:(13)(0) = 0 ..... ved at gange:0=0 ..... Ja, x = 4 virker
Vi får (3[4] + 1)([4] – 4) ?=? 0..... ved at erstatte:(13)(4 – 4) ?=? 0 ..... ved at dæmpe:(13)(0) = 0 ..... ved at gange:0=0 ..... Ja, x = 4 virker
Metode 2 af 3: Anvendelse af Abc-formlen

1. Flyt alle led til den ene side af ligningen og flet de lignende led. Flyt alle led til den ene side af lighedstegnet, mens termen x er positiv. Skriv ordene i faldende størrelsesorden, så x kommer først efterfulgt af x, derefter konstanten. Sådan gør du det:
- 4x - 5x - 13 =x -5
- 4x - x - 5x - 13 +5 = 0
- 3x - 5x - 8 = 0

2. Skriv abc-formlen ned. Dette er: {-b +/-√ (b - 4ac)}/2a

3. Bestem værdierne af a, b og c i andengradsligningen. Variablen -en er koefficienten af x, b er koefficienten for x og c er konstanten. For ligningen 3x -5x - 8 = 0, a = 3, b = -5 og c = -8. Skriv dette ned.

4. Erstat værdierne af a, b og c i ligningen. Nu hvor du kender værdierne af de tre variable, kan du bare sætte dem ind i ligningen, som vi viser her:

5. Beregn. Når du har udfyldt tallene, løser du problemet yderligere. Nedenfor kan du læse, hvordan det går videre:

6. Forenkle kvadratroden. Hvis tallet under det radikale tegn er et perfekt kvadrat eller også et kvadrattal, får du et helt tal med kvadratroden. I andre tilfælde skal du forenkle kvadratroden så meget som muligt. Hvis tallet er negativt, og du er sikker på, at det er hensigten, vil kvadratroden af tallet være mindre simpel. I dette eksempel er √(121) = 11. Du kan så skrive, at x =(5 +/- 11)/6.

7. Løs for de positive og negative tal. Når du er sluppet af med kvadratroden, kan du fortsætte, indtil du finder de negative og positive svar for x. Nu hvor du har (5 +/- 11)/6, kan du skrive de to muligheder ned:

8. Løs for de positive og negative svar. Beregn videre:

9. Forenkle. For at forenkle skal du dividere svarene med det største tal, der kan divideres med både tælleren og nævneren. Så divider den første brøk med 2 og den anden med 6, og du har løst x.
Metode 3 af 3: Opdeling af firkanten

1. Flyt alle led til den ene side af ligningen. Sørg for at -en af x er positiv. Sådan gør du det:
- 2x - 9 = 12x =
- 2x - 12x - 9 = 0
- I denne ligning, -en lig med 2, b er -12, og c er -9.

2. Flyt konstanten c til den anden side. Konstanten er den numeriske værdi uden en variabel. Flyt det til højre side af ligningen:

3. Divider de to sider med koefficienten af -en eller x-led. Hvis x ikke har noget led foran sig og har en koefficient med værdien 1, kan du springe dette trin over. I dette tilfælde skal du dividere alle led med 2, sådan her:

4. En del b med to, firkant det og tilføj resultaterne til begge sider af er-tegnet.Detb i dette eksempel er -6. Sådan gør du:

5. Forenkle begge sider. Faktorer termerne til venstre for at få (x-3)(x-3) eller (x-3). Tilføj vilkårene til højre for at få 9/2 + 9, eller 9/2 + 18/2, hvilket lægger op til 27/2.

6. Find kvadratroden af begge sider. Kvadratroden af (x-3) er simpelthen (x-3). Du kan også skrive kvadratroden af 27/2 som ±√(27/2). Derfor er x - 3 = ±√(27/2).

7. Forenkle kvadratroden og løs for x. For at forenkle ±√(27/2), se efter et perfekt kvadrat eller kvadrattal med tallene 27 eller 2 eller i deres faktorer. Kvadrattallet 9 kan findes i 27, fordi 9 x 3 = 27. For at fjerne 9 fra roden skal du skrive det som en separat rod og forenkle til 3, kvadratroden af 9. Lad √3 stå i brøkens tæller, fordi den ikke kan adskilles som en faktor fra 27, og gør 2 til nævneren. Flyt derefter konstanten 3 fra venstre side af ligningen til højre side og skriv dine to løsninger ned for x:
Tips
- Som du kan se, er det radikale tegn ikke helt forsvundet. Derfor er vilkårene i tælleren ikke slået sammen (de er ikke lige vilkår). Så det er meningsløst at opdele minusser og plusser. I stedet sørger vi ved at dividere, at enhver fælles faktor forsvinder – men "KUN" hvis faktoren er lig for begge konstanter, "OG" kvadratrodens koefficient.
Artikler om emnet "Løs andengradsligninger"
Оцените, пожалуйста статью
Populær