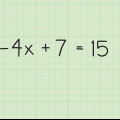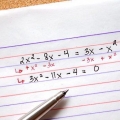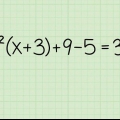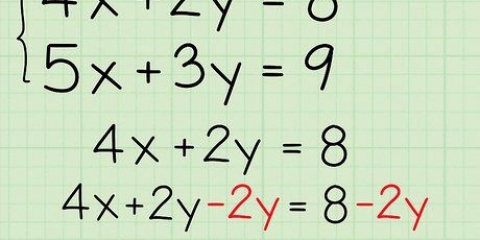3(x - 2/3) =
3(x - 2/3)(x -2/3) = 3[(x -2/3x -2/3x + 4/9)] 3(x - 4/3x + 4/9) 
-4/3 + 15/3 = 11/3.










Split square
Indhold
Kvadering er en nyttig teknik til at omskrive en andengradsligning, hvilket gør det lettere at overskue og løse. Du kan omskrive en firkant ved at omarrangere den i mere håndterbare stykker.
Trin
Metode 1 af 2: Del 1: Omskrivning af en standardligning

1. Skriv ligningen. Lad os antage, at du vil løse følgende ligning: 3x - 4x + 5.

2. Fjern koefficienten fra ligningen. Placer de 3 udvendige parenteser og divider hvert led undtagen konstanten med 3. 3x divideret med 3 er x og 4x divideret med 3 er 4/3x. Så den nye ligning ser således ud: 3(x - 4/3x) + 5. 5`eren er uden for parenteserne, fordi du ikke har divideret den med 3.

3. Divider det andet led med 2 og kvadrat. Det andet udtryk, også kaldet b-led i ligningen, er 4/3. Halver anden periode. 4/3 ÷ 2 eller 4/3 x 1/2 er lig med 2/3. Kvadrater dette led ved at gange både tælleren og nævneren med sig selv. (2/3) = 4/9. Skriv dette udtryk ned.

4. Addition og subtraktion. du har det her"ekstra" led, der er nødvendigt for at konvertere de første tre led i ligningen til et kvadrat. Men husk, at du tilføjede dette udtryk ved også at trække det fra ligningen. Det gør selvfølgelig ingen forskel blot at kombinere begreberne igen - så er du tilbage, hvor du startede. Den nye ligning skulle nu se sådan ud: 3( x - 4/3 x + 4/9 - 4/9) + 5.

5. Få det udtryk du har trukket uden for parentes. Fordi du allerede arbejder med de 3 uden for beslagene, er det ikke muligt bare at sætte -4/9 uden for beslagene. Først skal du gange det med 3. -4/9 x 3 = -12/9 eller -4/3. Hvis du har at gøre med en ligning, der kun indeholder en koefficient 1 ofx, kan du springe dette trin over.

6. Konverter termerne i parentes til en firkant. Din ligning ser nu sådan ud: 3(x -4/3x +4/9). Du arbejdede forfra for at få 4/9, hvilket faktisk er en anden måde at finde den faktor, der fuldender firkanten. Så du kan omskrive disse termer som: 3(x - 2/3). Du kan tjekke dette ved at gange, hvor du vil se, at du får den samme originale ligning som svaret igen.


7. Slå konstanterne sammen. Du har nu to konstanter, 3(x - 2/3) - 4/3 + 5. Alt du skal gøre nu er at tilføje -4/3 til 5 og dette giver 11/3 som svaret. Det gør du ved at give dem den samme nævner: -4/3 og 15/3, og derefter tilføje begge tællere for at få 11, mens nævneren holdes lig med 3.


8. Skriv ligningen på en anden form. Nu er du færdig. Den endelige ligning er 3(x - 2/3) + 11/3. Du kan eliminere 3`eren ved at dividere ligningen med 3, hvilket efterlader dig med følgende ligning:(x - 2/3) + 11/9.Du har nu skrevet ligningen i en anden form: a( x - h) + k, hvorved k konstanten er.
Metode 2 af 2: Anden del: Løsning af en andengradsligning

1. Bemærk opgaven. Lad os antage, at du vil løse følgende ligning: 3x + 4x + 5 = 6

2. Læg konstanterne sammen og placer dem til venstre for lighedstegnet. Konstante led er de udtryk uden en variabel. I dette tilfælde har du 5 til venstre og 6 til højre. Du vil flytte 6 til venstre, så træk 6 fra begge sider af ligningen. Dette efterlader 0 til højre (6-6) og -1 til venstre (5-6). Ligningen ser nu sådan ud: 3x + 4x - 1 = 0.

3. Tag kvadratets koefficient uden for parenteserne. I dette tilfælde er 3 koefficienten for x. For at udelukke 3 fra parentes skal du fjerne 3, placere det resterende led i parentes og dividere hvert led med 3. Så 3x ÷ 3 = x, 4x ÷ 3 = 4/3x og 1 ÷ 3 = 1/3. Ligningen ser nu sådan ud: 3(x + 4/3x - 1/3) = 0.

4. Divider med konstanten, du lige har sat i parentes. Med dette slipper du endelig for de irriterende 3 uden for beslagene. Ved at dividere hvert led med 3, kan det elimineres uden at ændre ligningen. Nu har du: x + 4/3x - 1/3 = 0

5. Divider det andet led med 2 og kvadrat. Tag nu anden periode, 4/3, de b sigt og dividere med 2. 4/3 2 eller 4/3 x 1/2, er 4/6 eller 2/3. Og 2/3 i anden er 4/9. Når du er færdig med dette, skal du skrive det til venstre og højre for ligningen, fordi du stort set lige har tilføjet et nyt udtryk. Du skal gøre dette på begge sider af ligningen. Ligningen ser nu sådan ud: x + 4/3 x + 2/3 - 1/3 = 2/3

6. Flyt den oprindelige konstant til højre side af ligningen og føj den til det udtryk, der allerede er der. Flyt konstanten, -1/3, til højre for at gøre den til 1/3. Føj dette til det andet udtryk, 4/9 eller 2/3. Find det mindste fælles multiplum, så 1/3 og 4/9 kan lægges sammen. Dette går sådan her: 1/3 x 3/3 = 3/9. Tilføj nu 3/9 til 4/9, så du har 7/9 på højre side af ligningen. Dette giver: x + 4/3 x + 2/3 = 4/9 + 1/3 og derefter x + 4/3 x + 2/3 = 7/9.

7. Skriv venstre side af ligningen som et kvadrat. Da du allerede har brugt en formel til at finde det manglende udtryk, er det sværeste allerede gjort. Alt du skal gøre er at sætte x og halvdelen af den anden koefficient i parentes og firkante den, sådan her :(x + 2/3). Bemærk, at faktorisering af kvadratet giver 3 led: x + 4/3 x + 4/9. Ligningen ser nu sådan ud: (x + 2/3) = 7/9.

8. Tag kvadratroden af begge sider af ligningen. På venstre side af ligningen er kvadratroden af (x + 2/3) lig med x + 2/3. Højre side giver +/- (√7)/3. Kvadratroden af nævneren 9 er 3, og kvadratroden af 7 er √7. Glem ikke at skrive +/-, fordi en kvadratrod af et tal kan være positiv eller negativ.

9. Sæt variablen til side. For at isolere variablen x fra resten skal du flytte konstanten 2/3 til højre side af ligningen. Du har nu to mulige svar for x:+/- (√7)/3 - 2/3. Dette er dine to svar. Du kan lade det være sådan eller uddybe kvadratroden, hvis du bliver bedt om et svar uden radikal.
Tips
- Sørg for at sætte +/- de rigtige steder ellers får du kun ét svar.
- Selvom du kender kvadratrodsformlen, kan det ikke skade at øve dig i at dividere kvadrater eller regne andengradsligninger ud i ny og næ. På den måde ved du med sikkerhed, at du ved, hvordan du gør det, når det er nødvendigt.
Artikler om emnet "Split square"
Оцените, пожалуйста статью
Populær