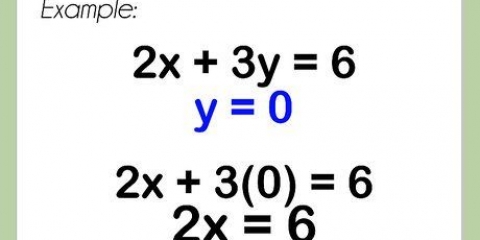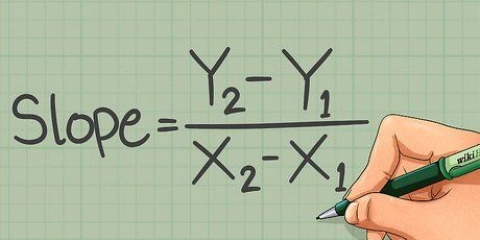Beregning af skæringspunktet mellem to linjer (med billeder)

Indhold

Trin
- Metode 1 af 2: Bestemmelse af skæringspunktet mellem to rette linjer
- Metode 2 af 2: Opgaver med andengradsligninger
Tips

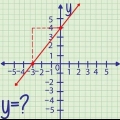
Når rette linjer skærer hinanden på en todimensional graf, gør de det ved kun ét punkt, angivet med koordinaterne x og y. Da begge linjer passerer gennem det punkt, ved du, at x- og y-koordinaterne skal opfylde begge ligninger. Med et par ekstra teknikker kan du finde skæringspunkterne mellem parabler og andre kvadratiske kurver ved hjælp af samme logik.

Trin

Metode 1 af 2: Bestemmelse af skæringspunktet mellem to rette linjer

1. Skriv ligningen for en linje med y til venstre. Ændre om nødvendigt ligningen, så y er isoleret på den ene side af lighedstegnet. Hvis ligningen er skrevet med f(x) eller g(x) i stedet for y, adskilles dette led. Husk, at du kan eliminere termer ved at udføre den samme handling på begge sider.

Er ligningerne ukendte, så afgør det baseret på de givne oplysninger.
Eksempel: Antag, at du har to linjer $y = x + 3$ $y=x+3$ og $y - 12 = - 2 x$ $y-12=-2x$ . For at adskille y i den anden ligning skal du tilføje 12 til hver side: $y = 12 - 2 x$ $y=12-2x$

Billede med titlen Algebraisk Find skæringspunktet mellem to linjer Trin 2

2. Sørg for, at de rigtige sider af ligningerne er ens. Vi leder efter et punkt, hvor de to linjer har samme x- og y-værdier; dette er det punkt, hvor linjerne skærer hinanden. Begge ligninger har kun et y til venstre, så vi ved, at de højre sider er lig med hinanden. Skriv en ny ligning, der viser dette.

Eksempel: vi ved det

y = x + 3

$y=x+3$ og

y = 12 - 2 x

$y=12-2x$ , og dermed $x + 3 = 12 - 2 x$ $x+3=12-2x$ .

Billede med titlen Algebraisk Find skæringspunktet mellem to linjer Trin 3

3. Løs x i ligningen. Den nye ligning har kun én variabel, x. Løs dette med algebra, ved at udføre den samme operation på begge sider. Find x-leddene på hver side af ligningen, og placer dem i formen x = __ (hvis det ikke er muligt, fortsæt med at læse i slutningen af dette afsnit).

Eksempel:

x + 3 = 12 - 2 x

$x+3=12-2x$

telefon

2 x

$2x$ på hver side:

3 x + 3 = 12

$3x+3=12$

Træk 3 fra hver side:

3 x = 9

$3x=9$

Divider hver side med 3:

x = 3

$x=3$ .

Billede med titlen Algebraisk Find skæringspunktet mellem to linjer Trin 4

4. Brug denne x-værdi til at løse for y. Vælg ligningen for hver linje. Erstat hvert x i ligningen med det svar, du fandt. Løs nu for y.

Eksempel:

x = 3

$x=3$ og

y = x + 3

$y=x+3$

y = 3 + 3

$y=3+3$

y = 6

$y=6$

Billede med titlen Algebraisk Find skæringspunktet mellem to linjer Trin 5

5. Tjek dit arbejde. Det er klogt at sætte din x-værdi ind i den anden ligning for at se, om du får det samme resultat. Hvis du får en anden løsning til y, skal du gå tilbage og tjekke dit arbejde for fejl.

Eksempel:

x = 3

$x=3$ og

y = 12 - 2 x

$y=12-2x$

y = 12 - 2 (3)

$y=12-2(3)$

y = 12 - 6

$y=12-6$

$y = 6$ $y=6$

Dette er det samme svar som tidligere opnået. Vi lavede ingen fejl.

Billede med titlen Algebraisk Find skæringspunktet mellem to linjer Trin 6

6. Skriv krydsets x- og y-koordinater ned. Du har nu løst for x-værdien og y-værdien af skæringspunktet mellem de to linjer. Skriv punktet som en koordinat med x-værdien som det første tal.

Eksempel:

x = 3

$x=3$ og

y = 6

$y=6$

De to linjer skærer hinanden i punktet (3.6).

Billede med titlen Algebraisk Find skæringspunktet mellem to linjer Trin 7

7. Behandle usædvanlige resultater. Nogle ligninger gør det umuligt at løse x. Dette betyder ikke nødvendigvis, at du har lavet en fejl. Der er to måder, hvorpå et par linjer kan føre til en speciel løsning:

Hvis de to linjer er parallelle, vil de ikke skære hinanden . X-leddene kan elimineres, og din ligning kan forenkles til en ugyldig ligning (som f.eks

0 = 1

$0=1$ ). Bemærk her`linjerne skærer ikke hinanden eller ikke en gyldig løsning` hvis du svarer.

Hvis de to ligninger beskriver den samme linje, så `skærer` de hinanden overalt. Du kan eliminere x-leddene og forenkle din ligning til en gyldig ligning (f.eks

3 = 3

$3=3$ ). Skriv ned `de to linjer er ens` som svar.

Metode 2 af 2: Opgaver med andengradsligninger

Billede med titlen Algebraisk Find skæringspunktet mellem to linjer Trin 8

1. Lær at genkende andengradsligninger. I en andengradsligning er der en eller flere variable i andengradsform (

x 2

$x^{2}$ eller

y 2

$y^{2}$ ), og der er ingen højere magter. Linjerne repræsenteret af ligninger er buede og kan derfor skære en ret linje i 0, 1 eller 2 punkter. I denne del lærer du, hvordan du finder skæringspunkterne for et sådant problem.

Udarbejd ligninger inden for parentes for at se, om de er kvadratiske. For eksempel, $y = (x + 3) (x)$ $y=(x+3)(x)$ er kvadratisk, fordi du kan sætte det uden for parentes, hvis $y = x 2 + 3 x .$ $y=x^{2}+3x$
At have ligninger af en cirkel eller en ellipse begge -en $x 2$ $x^{2}$ som en $y 2$ $y^{2}$ semester. Hvis du finder disse særlige tilfælde vanskelige, så læs videre på Tips i slutningen af denne artikel.

Billede med titlen Algebraisk Find skæringspunktet mellem to linjer Trin 9

2. Skriv ligningerne i form af y. Om nødvendigt omskriv hver ligning, så y er på den ene side.

Eksempel: Find skæringspunktet mellem

x 2 + 2 x - y = - 1

$x^{2}+2x-y=-1$ og

y = x + 7

$y=x+7$ .

Omskriv andengradsligningen i form af y:

$y = x 2 + 2 x + 1$ $y=x^{2}+2x+1$ og $y = x + 7$ $y=x+7$ .

Dette eksempel har en andengradsligning og en lineær ligning. Opgaver med to andengradsligninger løses på samme måde.

Billede med titlen Algebraisk Find skæringspunktet mellem to linjer Trin 10

3. Kombiner de to ligninger for at eliminere y. Hvis du har lavet begge ligninger lig med y, så ved du, at de to ligninger uden y er lig med hinanden.

Eksempel:

y = x 2 + 2 x + 1

$y=x^{2}+2x+1$ og

y = x + 7

$y=x+7$

$x 2 + 2 x + 1 = x + 7$ $x^{2}+2x+1=x+7$

Billede med titlen Algebraisk Find skæringspunktet mellem to linjer Trin 11

4. Omarranger den nye ligning, så den ene side er lig med nul. Brug almindelige matematiske metoder til at få alle led på den ene side af ligningen. Dette er den nødvendige opsætning af problemerne for at kunne løse dem i næste trin.

Eksempel:

x 2 + 2 x + 1 = x + 7

$x^{2}+2x+1=x+7$

Træk x fra hver side:

x 2 + x + 1 = 7

$x^{2}+x+1=7$

Træk 7 fra hver side:

$x 2 + x - 6 = 0$ $x^{2}+x-6=0$

Billede med titlen Algebraisk Find skæringspunktet mellem to linjer Trin 12

5.Løs andengradsligningen. Hvis du har en side lig nul, er der tre måder at løse andengradsligningen på. Alle foretrækker en anden metode. Du kan læse mere om andengradsformlen for `dele kvadratet`, eller du kan følge dette eksempel yderligere for det faktorisere metode:

Eksempel:

x 2 + x - 6 = 0

$x^{2}+x-6=0$

Formålet med factoring er at bestemme de to faktorer ganget sammen for at producere denne ligning. Fra den første periode ved vi det

x 2

$x^{2}$ kan opdeles i x og x. Skriv (x )(x ) = 0 for at vise dette.

Sidste termin er -6. Skriv ned hvert par faktorer, der ganges for at give -6 som produktet:

- 6 * 1

$-6*1$ ,

- 3 * 2

$-3*2$ ,

- 2 * 3

$-2*3$ , og

- 1 * 6

$-1*6$ .

Mellemleddet er x (som du kan skrive som 1x). Læg hvert par faktorer sammen for at få 1 som svar. Det rigtige par af faktorer er

- 2 * 3

$-2*3$ , fordi

- 2 + 3 = 1

$-2+3=1$ .

Udfyld hullerne i dit svar med disse få faktorer: $(x - 2) (x + 3) = 0$ $(x-2)(x+3)=0$ .

Billede med titlen Algebraisk Find skæringspunktet mellem to linjer Trin 13

6. Hold øjnene åbne for to løsninger til x. Hvis du arbejder for hurtigt, kan du finde ét svar på problemet uden at indse, at der er et andet. Sådan finder du de to x-værdier for linjer, der skærer hinanden i to punkter:

Eksempel (faktor): Vi ender med ligningen

(x - 2) (x + 3) = 0

$(x-2)(x+3)=0$ . Hvis begge faktorer i parentes er lig med 0, så er ligningen sand. Den ene løsning er

x - 2 = 0

$x-2=0$ → $x = 2$ $x=2$ . Den anden løsning er

x + 3 = 0

$x+3=0$ → $x = - 3$ $x=-3$ .

Eksempel (kvadratligning eller dividerende kvadrat): Hvis du bruger en af disse metoder til at løse ligningen, kommer der en kvadratrod. For eksempel bliver vores ligning

x = (- 1 + \sqrt{25}) / 2

$x=(-1+{sqrt{25}})/2$ . Husk, at du kan forenkle en kvadratrod til to forskellige løsninger:

\sqrt{25} = 5 * 5

${sqrt{25}}=5*5$ , og

\sqrt{25} = (- 5) * (- 5)

${sqrt{25}}=(-5)*(-5)$ . Skriv to ligninger, en for hver mulighed, og løs for x for hver af dem.

Billede med titlen Algebraisk Find skæringspunktet mellem to linjer Trin 14

7. Løs problemer med én eller nul løsninger. To linjer, der næsten ikke rører hinanden, har et skæringspunkt, og to linjer, der aldrig rører hinanden, har nul. Du kan genkende dem på følgende måder:

Én løsning: Problemerne kan opdeles i to identiske faktorer ((x-1)(x-1) = 0). Indtastet i den kvadratiske formel bliver kvadratroden

\sqrt{0}

${sqrt{0}}$ . Du skal kun løse én ligning.

Der er ingen reel løsning: Der er ingen faktorer, der opfylder kravene (notering til mellemlang sigt). Indtastet i den kvadratiske formel får du et negativt tal under radikalet (som f.eks

\sqrt{- 2}

${sqrt{-2}}$ ). Skriv `ingen løsning` som dit svar.

Billede med titlen Algebraisk Find skæringspunktet mellem to linjer Trin 15

8. Sæt x-værdierne tilbage i den oprindelige ligning. Når du har x-værdien af skæringspunktet, skal du sætte den tilbage i en af ligningerne du startede med. Løs for y for at finde y-værdien. Hvis der er en anden x-værdi, gentag også denne værdi.

Eksempel: Vi har fundet to løsninger,

x = 2

$x=2$ og

x = - 3

$x=-3$ . En af vores linjer har ligningen

y = x + 7

$y=x+7$ . erstatning

y = 2 + 7

$y=2+7$ og

y = - 3 + 7

$y=-3+7$ , og løs hver ligning, så du får

y = 9

$y=9$ og

y = 4

$y=4$ hvis du får svar.

Billede med titlen Algebraisk Find skæringspunktet mellem to linjer Trin 16

9. Skriv svaret som koordinater. Nu skriver du svaret som koordinater, med krydsets x-værdi og y-værdi. Hvis du har to svar, skal du sørge for at matche den rigtige x-værdi med hver y-værdi.

Eksempel: Når vi

x = 2

$x=2$ input, får vi

y = 9

$y=9$ , således at ét skæringspunkt er lig med (2, 9). Vi gør det samme for den anden løsning, og dette giver os skæringspunktet (-3, 4) på.

Tips

Ligninger for en cirkel eller ellipse har en $x 2$ $x^{2}$ semester og -en $y 2$ $y^{2}$ semester. For at finde skæringspunktet mellem en cirkel og en ret linje skal du løse for x inde i den lineære ligning. Erstat x-løsningen i cirkelligningen, og andengradsligningen er blevet meget nemmere. Disse problemer kan have 0, 1 eller 2 løsninger, som allerede angivet i metoderne ovenfor.
En cirkel og en parabel (eller enhver anden andengradsligning) kan have 0, 1, 2, 3 eller 4 løsninger. Find variablen, som er et kvadrat i begge ligninger — lad os sige, at dette er x. løs $x 2$ $x^{2}$ på og erstatte svaret med $x 2$ $x^{2}$ i den anden ligning. Løs y for at finde 0, 1 eller 2 løsninger. Sæt hver løsning tilbage i den oprindelige andengradsligning og løs for x. Hver af disse kan have 0, 1 eller 2 løsninger.