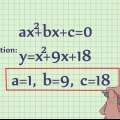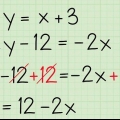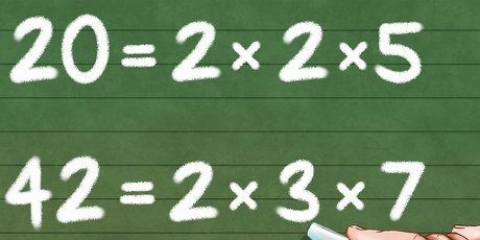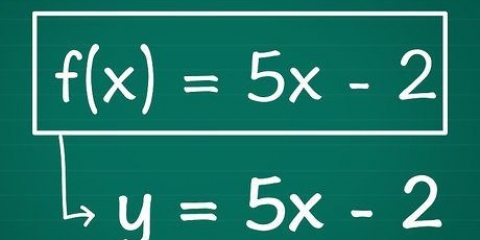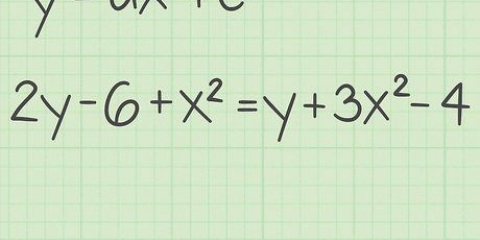I eksempelligningen ovenfor, hvis du dividerer begge sider med 2, 2x = 6, får du 2/2 x = 6/2 eller x = 3. Dette er x-skæringspunktet for ligningen 2x + 3y = 6. Du kan bruge de samme trin til ligninger med formen ax^2 + by^2 = c. I dette tilfælde, hvis du indtaster 0 for y, får du x^2 = c/a, og efter at du har fundet værdien til højre for lighedstegnet, skal du finde roden af x-kvadrat. Dette giver dig 2 værdier, 1 positiv og 1 negativ, som summerer til 0. 

Factoring er at opdele en andengradsligning i 2 enklere algebraiske udtryk, som, når de ganges sammen, producerer andengradsligningen. Ofte kan værdierne af a og c være nøglen til at finde de rigtige faktorer. Da 2 gange 5 er lig med 10, er den absolutte værdi af c, og fordi den absolutte værdi af b er mindre end den af c, er 2 og 5 sandsynligvis de numeriske komponenter af de korrekte faktorer. Da 5 minus 2 er lig med 3, er de korrekte faktorer x + 5 og x - 2. Hvis du udfylder faktorerne for andengradsligningen, (x + 5)(x - 2) = 0, er 2x skæringspunkterne -5 (-5 + 5 = 0) og 2 (2 - 2 = 0). Hvis du bruger den kvadratiske formel, skal du indsætte værdierne for a, b og c fra den kvadratiske formel i formlen (-b + eller - W (b^2 - 4 ac))/2a (hvor W er kvadratet root ) for at finde værdien eller værdierne for x. Hvis du tilslutter værdierne 1, 3 og -10 i denne ligning, får du (-3 + eller - W (3^2 - 4(1)(-10)))/2(1). Værdien inden for W-parenteserne kommer ud til 9 -(-40) eller 9+40, hvilket er 49, så ligningen kommer ud til (-3 + eller - 7)/2, hvilket fører til (-3 + 7 ) /2 eller 4/2, som er 2, og (-3 -7)/2 eller -10/2, som er -5. I modsætning til de simple 2-variable ligninger beskrevet i det foregående afsnit, tegnes andengradsligninger på en koordinatgraf som en parabel (en buet linje, der ligner en "DU" eller "V") i stedet for en lige linje. Kvadratiske ligninger kan ikke have x skæringspunkter, 1 x skæringspunkter eller 2 x skæringspunkter.
Find skæringspunktet med x-aksen
Indhold
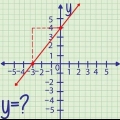
I algebra har 2-dimensionelle grafer med koordinater en vandret akse eller x-akse og en lodret akse eller y-akse. De steder, hvor linjer, der repræsenterer en række værdier, skærer disse akser, kaldes skæringspunkter. Y-skæringspunktet er, hvor linjen skærer y-aksen, og x-skæringspunktet er, hvor linjen skærer x-aksen. At finde x-skæringspunktet med algebra kan være enkelt eller kompliceret, afhængigt af om ligningen kun har 2 variable eller er kvadratisk. Trinene nedenfor viser, hvordan det virker for begge typer ligninger.
Trin
Metode 1 af 2: Simple ligninger med 2 variable

1. Erstat værdien af y med 0. På det punkt, hvor værdilinjen krydser den vandrette akse, har y en værdi på 0.
- I eksempelligningen, hvis du erstatter 2x + 3y = 6, y med 0, ændres ligningen til 2x + 3(0) = 6, så stort set kun 2x = 6.

2. Find løsningen for x. Dette betyder normalt at dividere begge sider af ligningen med koefficienten for x for at give den en værdi på 1.
Metode 2 af 2: Til andengradsligninger

1. Sæt ligningen på formen ax^2 + bx + c = 0. Dette er standardformen til at skrive en andengradsligning, hvor a er koefficienten for x-kvadrat, b er koefficienten for x, og c er en rent numerisk værdi.
- Til eksemplet i dette afsnit bruger vi ligningen x^2 +3x - 10 = 0.

2. Løs ligningen for x. Der er flere måder at løse en andengradsligning på. De 2, vi har at gøre med her, er factoring og bruger den kvadratiske formel.
Tips
- Hvis i eksemplet sammenligning nedenfor "Simple ligninger med 2 variable" Hvis du indtaster et 0 for x i stedet for y, kan du finde ud af værdien af y-skæringspunktet.
Artikler om emnet "Find skæringspunktet med x-aksen"
Оцените, пожалуйста статью
Populær