Find det mindste fælles multiplum af to tal

Indhold

Trin
Tips
Fornødenheder

Det mindste fælles multiplum (KGB) af en gruppe af tal er det mindste tal, der er et multiplum af alle tal i gruppen. For eksempel er LCF for 16 og 20 80; 80 er det mindste tal, der både er et multiplum af 16 og et multiplum af 20. Du kan finde LCF for to eller flere tal ved hjælp af forskellige metoder. Hvis du vil vide, hvordan du finder LCF for to eller flere tal, skal du følge disse trin.

Trin

Metode 1 af 4: Primfaktorisering

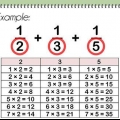
1. Bestem primfaktorerne for begge tal. Dette er en ideel metode til større tal. Det første trin i at finde det mindste fælles multiplum af to tal ved hjælp af denne metode er at indregne begge tal i primtal ganget for at få dette tal som et produkt. Du kan starte med at lave en liste over to tal (faktorer) ganget sammen for at producere det tal og derefter indregne dem i deres primfaktorer. Antag, at du vil finde det mindste fælles multiplum af 20 og 42. Sådan faktoriseres det. 20 = 2 x 2 x 542 = 2 x 3 x 7

Billede med titlen Find det mindste fælles multiplum eller to tal Trin 2

2. Skriv ned hvilket primtal der oftest forekommer i hvert tals primfaktorer. Her er en liste over tal, der forekommer oftest for hvert primtal i det foregående eksempel 2 → 2 gange3 → 1 gang5 → 1 gang7 → 1 gang

3. Multiplicer alle faktorer sammen . Her er hvad du skal gøre for at finde eksemplets EKG:

2 x 2 x 3 x 5 x 7 = 420.

Billede med titlen Find det mindste fælles multiplum eller to tal Trin 3Bullet1

LCF på 20 og 42 er 420.

Billede med titlen Find det mindste fælles multiplum eller to tal Trin 3Bullet2

Metode 2 af 4: List alle multipla af begge tal

Billede med titlen Find det mindste fælles multiplum eller to tal Trin 5

1. Angiv nogle multipla af det første tal i stigende rækkefølge. Dette er en ideel metode til mindre tal, især for tal mindre end 10. For større antal anbefales dette ikke, da dette kan blive vanskeligt. Antag, at du vil finde KGV af 5 og8. Du laver først en liste over multiplerne af 55 x 1 = 55 x 2 = 105 x 3 = 15

2. Skriv nu nogle multipla af det andet tal (8), i stigende rækkefølge.

8 x 1 = 8

8 x 2 = 16

8 x 3 = 24

Billede med titlen Find det mindste fælles multiplum eller to tal Trin 6

3. Prøv en række muligheder for begge tal, indtil du har fundet det mindste fælles multiplum. I nogle tilfælde kan du finde LCF`en efter et par forsøg for hvert nummer. Fortsæt i dette eksempel, indtil du finder et mindste fælles multiplum for 5 og 8. Det er din kgf

5 x 4 = 20

5 x 5 = 25

5 x 6 = 30

5 x 7 = 35

5 x 8 = 40

8 x 4 = 32

8 x 5 = 40

LCF på 5 og 8 er 40. Dette er det mindste fælles multiplum, fordi det er en først forekommende faktor af samme multiplum for både 5 og 8, og dermed LCF for disse tal.

Billede med titlen Find det mindste fælles multiplum eller to tal Trin 6Bullet1

Metode 3 af 4: Brug en fælles multipletabel

Billede med titlen Find det mindste fælles multiplum eller to tal Trin 7

1. Skriv tallene øverst i en tabel med fælles multipla. Efterlad lidt plads på venstre side af tallene, og så meget plads som muligt under tallene. Antag, at vi har tallene 18, 12 og 30. Skriv hvert tal i sin egen kolonne, øverst i tabellen.

Billede med titlen Find det mindste fælles multiplum eller to tal Trin 8

2. Skriv den mindst almindelige primfaktor af tallene i mellemrummet til venstre. Se efter den mindste primfaktor (såsom 2, 3 eller 5), som du kan faktorisere ud af alle tal. De er alle lige tal, så mindst 2 er muligt.

Billede med titlen Find det mindste fælles multiplum eller to tal Trin 9

3. Divider hvert af de tal, du antager, med den fælles primfaktor. Skriv kvotienten under hvert tal. Sådan kommer det til at se ud:

18/2 = 9, så skriv 9 under 18.

12/2 = 6, så skriv 6 under 12.

30/2 = 15, så skriv 15 under 30.

Billede med titlen Find det mindste fælles multiplum eller to tal Trin 10

4. Gentag processen med at faktorisere og dividere med den laveste primfaktor, indtil der ikke er nogen faktorer tilbage. Gentag for tallene 9, 6 og 15.

Faktor 3 ud af disse tal. 3 er den mindste primtal her, det mindste primtal deleligt med begge tal.

Billede med titlen Find det mindste fælles multiplum eller to tal Trin 10Bullet1

Divider alle tre tal med 3 og skriv resultatet under disse tal.

Billede med titlen Find det mindste fælles multiplum eller to tal Trin 10Bullet2

9/3 = 3, så du skriver en 3 under 9; 6/3 = 2, så du skriver en 2 under 6; 15/3 = 5, så du skriver en 5 under 15.

Billede med titlen Find det mindste fælles multiplum eller to tal Trin 10Bullet3

Billede med titlen Find det mindste fælles multiplum eller to tal Trin 11

5. Hvis to af tallene stadig deler en fælles primfaktor, fortsæt denne procedure, indtil ingen af de nederste tal har en fælles faktor. Hvad angår dette eksempel, er du nu færdig.

Antag som et eksempel, at de nederste tal er 2, 39 og 122, divider derefter 2 og 122 med 2, hvilket resulterer i en ny nederste række: 1, 39 og 61.

Billede med titlen Find det mindste fælles multiplum eller to tal Trin 12

6. Gang alle tallene i den første kolonne med de fælles primfaktorer, med tallene i bunden af alle de andre kolonner. Dette er KGV. I dette eksempel er produktet af kolonnen fælles faktorer lig med 6 (2 x 3). Gang 6 med tallene i bunden af de andre kolonner: 6 x 3 x 2 x 5 = 180.

LCF på 18, 12 og 30 er 180.

Billede med titlen Find det mindste fælles multiplum eller to tal Trin 12Bullet1

Metode 4 af 4: Euklids algoritme

1. Brug Euklids algoritme til at finde den største fælles divisor (GGD) af to tal. Antag de to tal i et eksempel210 og 45 er. Her er et eksempel på, hvordan man bruger Euklids algoritme til at finde GGD for begge tal:

Divider det første tal med det andet: 210/45 = 4 (rest 30). Det betyder, at 210 = 4 x 45 + 30.

Billede med titlen Find det mindste fælles multiplum eller to tal Trin 13Bullet1

Divider derefter det andet tal (45) med resten (30). 45/30 = 1 (resten 15). Så 45 = 1 x 30 + 15.

Billede med titlen Find det mindste fælles multiplum eller to tal Trin 13Bullet2

Del derefter resten fra det første trin (30) med resten fra det andet trin (15). 30/15 = 2 (rest 0). Så 30 = 2 x 15 + 0.

Billede med titlen Find det mindste fælles multiplum eller to tal Trin 13Bullet3

GGD på 210 og 45 er 15.

Billede med titlen Find det mindste fælles multiplum eller to tal Trin 13Bullet4

Du kan altid bruge denne metode til at finde GGD - bare stop med at dele, når du når en rest på 0.

Billede med titlen Find det mindste fælles multiplum eller to tal Trin 14

2. Gang de to oprindelige tal. 210 x 45 = 9.450

Billede med titlen Find det mindste fælles multiplum eller to tal Trin 15

3. Divider resultatet med GGD for begge tal. 9.450/15 = 630. 630 er LCF på 210 og 45.

Billede med titlen Find det mindste fælles multiplum eller to tal Trin 16

4. Brug Euklids algoritme til at finde LCF for tre tal. For at gøre dette skal du blot søge efter GCD for to tal og derefter bruge den GGD til at finde VCF for disse to tal og det tredje tal.

Tips

Hvis du vil vide, om VCF er mindre eller større end produktet, så brug denne metode: Hvis GGD er 1, så er VCF produktet. Hvis GGD er større end 1, vil VCGV være mindre end produktet.
KGV har mange anvendelsesmuligheder. Det mest almindelige er, at når du tilføjer eller trækker brøker fra, skal de have samme nævner; hvis dette ikke er tilfældet, bliver du nødt til at gøre dem eponyme, så de har samme nævner. Den bedste måde at gøre dette på er at lede efter den mindste fællesnævner - som simpelthen er den samme som LCF for nævnerne. For at beregne 1/6 + 3/8, lad os for eksempel finde LCF for 6 og 8, som er 24, og derefter konvertere hver brøk, så begge nævnere er lig med 24, så summen ser sådan ud: 4/24 + 24/9. Vi kan nu blot beregne dette, ved at lægge tælleren sammen, med svaret: 13/24.
Hvis du skal finde LCF for mere end 2 numre, så skal din metode ovenfor ændres lidt, da den kun virker for 2 numre på samme tid. For at finde LCF på 16, 20 og 32 starter vi med at finde LCF på 16 og 20 (som er lig med 80) og derefter LCF på 80 og 32, som kommer ud til 160.
For at finde CHF på 16 og 20 tager vi for eksempel GGD på 16 og 20, som kommer ud til 4. 16 × 20 = 320 og 320 ÷ 4 = 80, så 80 er KGV.
Hvis du vil lave en brøkdel af samme navn, skal du vide, hvor mange gange hver nævner går i LCF. Ved at bruge denne metode kan du finde omregningsfaktoren ved at gange alle tallene i bunden af alle de andre kolonner (undtagen den første, hvor alle primfaktorerne er angivet). Så for at konvertere 18 til 180 skal du gange det med 2 og 5. For at konvertere 12 til 180 skal du gange det med 3 og 5.For at konvertere 30 til 180 skal du gange det med 3 og 2.