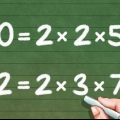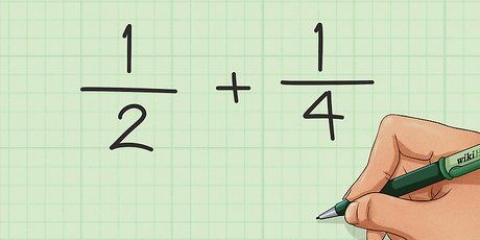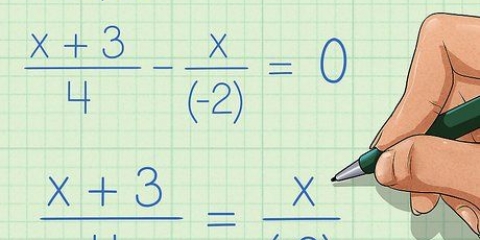Find det mindste fælles multiplum af to nævnere

Indhold

Trin
Fornødenheder

At tilføje eller trække brøker med forskellige nævnere. det er nødvendigt først at finde det mindste fælles multiplum af disse to tal. Dette er det mindste multiplum af enhver nævner i en ligning. Her er nogle forskellige metoder, du kan bruge til at finde lcm`en og bruge dem til at løse brøkproblemer.

Trin

Metode 1 af 4: List multipla

1. Angiv multipla af hver nævner. Hver liste skal bestå af nævneren af brøken ganget med 1, 2, 3, 4 osv.

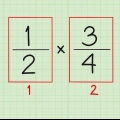
Eksempel: 1/2 + 1/3 + 1/5
Multipler af 2: 2 *1=2; 2 *2=4; 2 *3=6; 2 *4=8; 2 *5=10; 2 *6=12; 2 *7=14; etc.
Multipler af 3: 3 *1=3; 3 *2=6; 3 *3=9; 3 *4=12; 3 *5=15; 3 *6=18; 3 *7=21; etc.
Multipler af 5: 5 *1=5; 5 *2=10; 5 *3=15; 5 *4=20; 5 *5=25; 5 *6=30; 5 *7=35; etc.

Billede med titlen Find den mindste fællesnævner Trin 2

2. Find det mindste fælles multiplum. Scan gennem hver liste og fremhæv ethvert fælles multiplum af begge nævnere. Efter at have bestemt de fælles multipla, skal du bestemme, hvilken der er den mindste.

Bemærk, at hvis der i øjeblikket ikke er et fælles multiplum, skal du fortsætte, indtil du finder et multiplum, der er gyldigt for begge nævnere.

Eksempel: 2 *15=30; 3 *10=30; 5 *6=30

kgv=30

Billede med titlen Find den mindste fællesnævner Trin 3

3. Omskriv det oprindelige problem. For at skrive hver brøk i denne sum, så den har samme værdi som den oprindelige opgave, er det nødvendigt at gange brøkens tæller og nævner med den passende værdi, som svarer til det fælles multiplum.

Eksempel: 15 *(1/2); 10 *(1/3); 6 *(1/5)

Ny sum: 15/30 + 10/30 + 6/30

Billede med titlen Find den mindste fællesnævner Trin 4

4. Løse. Når du har fundet LCF`en og brøkerne er blevet ændret, burde du være i stand til at løse dette problem uden problemer.

Eksempel: 15/30 + 10/30 + 6/30=31/30=1 1/30

Metode 2 af 4: Brug af den største fælles divisor

Billede med titlen Find den mindste fællesnævner Trin 5

1. Find den største fælles divisor for hver nævner. Find ud af, om der er den største fælles divisor for begge nævnere ved at finde ud af, hvilke tal der er delelige med nævnerne.

Eksempel: 3/8 + 5/12
Faktorer af 8: 1, 2, 4, 8
Faktorer af 12: 1, 2, 3, 4, 6, 12

Billede med titlen Find den mindste fællesnævner Trin 6

2. Identificer den største fælles divisor mellem begge nævnere. Sæt en cirkel om alle GCD`er efter at have fundet faktorerne for hver nævner. Den største af GCD`erne er den største fællesnævner, som du kan bruge til at løse problemet yderligere.

I vores eksempel deler 8 og 12 nævneren 1, 2 og 4.

Den største fælles divisor er 4.

3. Multiplicer nævnerne sammen. Gå til næste trin ved at gange de to nævnere sammen.

Eksempel: 8 *12=96

Billede med titlen Find den mindste fællesnævner Trin 7

4. Del af gcd. Når du har fundet produktet af begge nævnere, dividerer du dette med det tidligere fundne gcd. Resultatet af denne division er dit mindste fælles multiplum.

Eksempel: 96 / 4=24

Billede med titlen Find den mindste fællesnævner Trin 8

5. Omskriv det oprindelige problem. Omskriv tællerne ved at gange dem med det samme tal, det tog for at gøre de tilsvarende nævnere lig med lcg. Find faktoren for hver brøk ved at dividere lcm med den oprindelige nævner.

Eksempel: 24 / 8=3; 24/12=2

3 *(3/8)=9/24; 2 *(5/12)=10/24

24/9 + 24/10

Billede med titlen Find den mindste fællesnævner Trin 9

6. Løs problemet. Med den fundet kgv skulle det nu være muligt at addere og subtrahere uden problemer.

Eksempel: 9/24 + 10/24=19/24

Metode 3 af 4: Indregning af fraktioner i primfaktorer

Billede med titlen Find den mindste fællesnævner Trin 10

1. Opdel nævnerne i primtal. Opdel hver nævner i en række primtal. Husk, at primtal er de tal, der ikke kan divideres med noget andet tal undtagen 1 og sig selv.

Eksempel: 1/4 + 1/5 + 1/12
De primære faktorer af 4: 2 *2
De primære faktorer af 5: 5
De primære faktorer for 12: 2 *2 *3

Billede med titlen Find den mindste fællesnævner Trin 11

2. Tæl antallet af gange, hvert primtal forekommer i sættet af primtal. Turf antallet af gange hvert primtal forekommer i primtalsfaktorerne for hver nævner.

Eksempel: Der er to 2-og i 4; nul 2-og i 5; to 2-og i 12

Der er nul 3-og i 4 og 5; -en 3 i 12

Der er nul 5-og i 4 og 12; -en 5 i 5

Billede med titlen Find den mindste fællesnævner Trin 12

3. Tag det største tal for ethvert primtal. Bemærk, hvor mange gange du har brugt hvert primtal.

Eksempel: Det største tal for 2 er to; det største antal for 3 er en; det største antal for 5 er en.

Billede med titlen Find den mindste fællesnævner Trin 13

4. Skriv dette som et eksempel nedenfor.

Eksempel: 2, 2, 3, 5

Billede med titlen Find den mindste fællesnævner Trin 14

5. Gang alle primtal på denne måde. Multiplicer primtallene fra den foregående serie. Produktet af disse tal er lig med lcm af den oprindelige opgave.

Eksempel: 2 *2 *3 *5=60

kgf=60

Billede med titlen Find den mindste fællesnævner Trin 15

6. Omskriv det oprindelige problem. Divider LCF med den oprindelige nævner. Multiplicer hver tæller med det samme tal, som er nødvendigt for at gøre den tilsvarende nævner til LCF.

Eksempel: 60/4=15; 60/5=12; 60/12=5

15 *(1/4)=15/60; 12 *(1/5)=12/60; 5 *(1/12)=5/60

15/60 + 12/60 + 5/60

Billede med titlen Find den mindste fællesnævner Trin 16

7. Løse. Med den fundne LCF og lignende nævnere er det blevet nemt at addere og trække brøkerne fra som normalt.

Eksempel: 15/60 + 12/60 + 5/60=32/60=8/15

Metode 4 af 4: Arbejde med heltal og blandede tal

Billede med titlen Find den mindste fællesnævner Trin 17

1. Konverter ethvert heltal og blandet tal til en uægte brøk. Konverter blandede tal til uægte brøker ved at gange hele tallet før brøken med nævneren og lægge tælleren til produktet. Konverter et heltal til en uægte brøk ved at placere det som en tæller i en brøk med nævneren `1`.

Eksempel: 8 + 2 1/4 + 2/3
8=8/1
2 1/4; 2 *4 + 1=8 + 1=9; 9/4
Omskrevet opgave: 8/1 + 9/4 + 2/3

Billede med titlen Find den mindste fællesnævner Trin 18

2. Find det mindste fælles multiplum af nævnerne. Anvend en af metoderne til at finde LCF for en almindelig brøk, som beskrevet ovenfor. Bemærk, at vi i dette eksempel bruger `Listing multiples`-metoden, opretter en liste med multipler for hver nævner og udleder lcm fra denne.

Bemærk, at du ikke behøver at angive multipla af 1 fordi hvert tal er et multiplum af 1.

Eksempel: 4 *1=4; 4 *2=8; 4 *3=12; 4 *4=16; etc.

3 *1=3; 3 *2=6; 3 *3=9; 3 *4=12; etc.

kgv=12

Billede med titlen Find den mindste fællesnævner Trin 19

3. Omskriv det oprindelige problem. I stedet for blot at gange nævneren er det nødvendigt også at gange tælleren med det tal, der skal til for at gøre nævneren til en lcg.

Eksempel: 12 *(8/1)=96/12; 3 *(9/4)=27/12; 4 *(2/3)=8/12

96/12 + 27/12 + 8/12