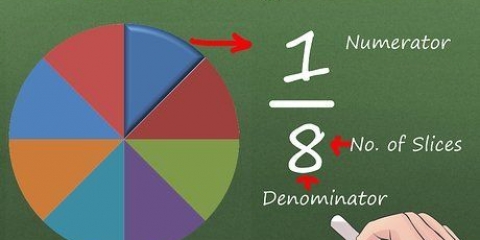
24: 1, 2, 3, 4, 6, 8, 12, 24. 32: 1, 2, 4, 8, 16, 32. gcd for 24 og 32 er 8, fordi 8 er det største tal, som både 24 og 32 er delelige med. 
24/8 = 3 32/8 = 4 Så den forenklede brøk er 3/4. 
3 * 8 = 24 4 * 8 = 32 Dette er den oprindelige fraktion igen, 24/32. Du kan også undersøge, om brøken ikke kan forenkles yderligere. Da 3 er primtal, kan den kun divideres med 1 og sig selv, så denne brøk kan ikke forenkles yderligere. 

24/2 = 12 32/2 = 16 Den nye, forenklede fraktion er 12/16. 
12/2 = 6 16/2 = 8 Den nye brøk er 6/8. 
6/2 = 3 8/2 = 4 Den nye fraktion bliver 3/4. 
Hvis du for eksempel vil forenkle brøken 10/40, starter du med at dividere tæller og nævner med 5, så 2/8. Du kan ikke dividere med 5 igen, men du kan dividere med 2, så det endelige svar bliver ¼. 
3/4 * 2/2 = 6/8 6/8 * 2/2 = 12/16 12/16 * 2/2 = 24/32. Bemærk, at du dividerede 24/32 med 2 * 2 * 2, hvilket er det samme som at dividere med 8, den største fælles divisor af 24 og 32. 

For eksempel: vi har brøken 24/60. Start med 24.Du bemærker: 24 -- 1, 2, 3, 4, 6, 8, 12, 24 Fortsæt derefter med 60.Du bemærker: 60 -- 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60 
I vores eksempel er det største tal divisoren 12. Så vi deler begge 24 og 60 med 12, hvilket gør brøken 2/5 - vores forenklede brøk! 

Så for 24 har du 2 x 2 x 2 x 3 = 24. Og for 60 har du 2 x 2 x 3 x 5 = 60 
Det vi står tilbage med er en 2 og en 5 – eller 2/5! Det samme svar fik vi med den forrige metode. Hvis både tæller og nævner er lige tal, så husk at dele tallet i to. Bliv ved med det, indtil de er for små til at deles yderligere.
Forenkle brøker
Indhold
Matematik behøver ikke at være svært, men det er ikke altid nemt at huske alle de forskellige principper og metoder. Selv de grundlæggende teknikker kan nogle gange glemmes. Så her er yderligere to metoder til at forenkle brøker.
Trin
Metode 1 af 4: Brug af den største fælles divisor

1. Angiv alle faktorer i tælleren og nævneren. Faktorerne for et givet tal er de tal, der ganges sammen danner dette tal. Eksempel 3 og 4 er begge faktorer på 12, fordi 3 x 4 = 12. For at liste alle faktorerne i et tal skal du finde ud af, hvilke tal alle går helt ind i det tal.
- Angiv faktorerne fra mindste til største og glem ikke 1. Dette er listen:
- 24: 1, 2, 3, 4, 6, 8, 12, 24.
- 32: 1, 2, 4, 8, 16, 32.

2. Find den største fælles divisor (gcd) for tælleren og nævneren. gcd er det største tal, som to tal, i dette tilfælde tælleren og nævneren, er delelige med. Når du har de to lister med faktorer klar, skal du bare finde det største tal (divisoren), der forekommer i begge lister.

3. Divider tæller og nævner med gcd. Nu hvor du har fundet gcd`en, skal du bare dividere tælleren og nævneren med dette tal for at forenkle din brøk så meget som muligt. Sådan fungerer det:

4. Tjek dit arbejde. Hvis du vil vide, om din forenkling er korrekt, skal du gange tælleren og nævneren for forenklingen med gcd for at sikre, at du får den oprindelige brøk tilbage som resultat. Sådan fungerer det:
Metode 2 af 4: Fortsæt med at dividere med et lille tal

1. Vælg et lille tal. Brug denne metode, vælg blot et lille tal, såsom 2, 3, 4, 5 eller 7, for at komme i gang. Se på brøkerne for at sikre, at tallet er deleligt mindst én gang med et hvilket som helst tal, du vælger. For eksempel, hvis du tager brøken 24/108, skal du ikke vælge 5, fordi det ikke passer til nogen af tallene. Men hvis du undersøger fraktionen 25/60, så er 5 et godt valg.
- I tilfælde af brøken 24/32 fungerer tallet 2 glimrende. Da begge tal er lige, er de også delelige med 2.

2. Divider tælleren og nævneren af en brøk med dette tal for at forenkle det. Sådan fungerede det:

3. gentag dette. Da begge tal stadig er lige, kan du fortsætte med at dividere med 2. Hvis et af tallene bliver ulige, kan du prøve at bruge et andet tal som divisor. Sådan fortsætter det:

4. Fortsæt med at dividere med 2, indtil du ikke kan komme længere.

5. Sørg for, at brøken ikke kan forenkles yderligere. Som i det foregående eksempel: 3 er prime, og ¾ kan derfor ikke forenkles yderligere. Hvis tælleren og nævneren for en brøk ikke kan divideres igen med det valgte tal, prøv et andet tal.

6. Tjek dit svar. Arbejd tilbage til udgangspunktet ved at gange 3/4 med 2/2 tre gange og tjek om svaret er lig med 24/32. Her kan du se dette uddybet:
Metode 3 af 4: Angiv divisorerne

1. Skriv din brøk ned. Efterlad et stort mellemrum på højre side af dit papir – det handler om at skrive faktorerne ned.

2. Angiv faktorerne for tælleren og nævneren. Sæt dem på separate lister. Det kan være nemmere, hvis listerne er justeret over hinanden. Start med 1 og gå derefter fra mindste til største og skriv parrene ned.

3. Find den største fælles divisor (gcd).Hvad er det største tal, der både er en divisor af tælleren og nævneren?? Uanset hvad det er, divider begge tal med det tal.
Metode 4 af 4: Brug af primfaktorer

1. Find primfaktorerne for tælleren og nævneren. EN "primtal" er et tal, der ikke kan divideres med noget andet heltal undtagen 1 og sig selv. 2, 3, 5, 7 og 11 er eksempler på primtal.
- Start med tælleren. Opdel 24 i faktor 2 og 12. fordi 2 er et primtal er du færdig med den gren med det samme! Opdel nu 12 i faktor 2 og 6. 2 er prime -- fint! Del nu de 6 i faktor 2 og 3. Nu har du 2, 2, 2 og 3 som primtal.
- Fortsæt med nævneren. Opdel 60 i faktor 2 og 30. Opdel 30 i faktor 2 og 15. Del 15 i 3 og 5, begge primtal. Nu har du følgende liste over primtal: 2, 2, 3 og 5.

2. Skriv primfaktorerne for tæller og nævner ned. Tag rækken af primtal, du har fundet, gang dem sammen. Gør dette for tæller og nævner. Dette gør det nemmere at se, hvad der sker.

3. Ignorer de lige faktorer. Ethvert par tal fra begge serier kan fjernes. I dette tilfælde har vi to par toere og et par treere. De kan fjernes!
Tips
- Hvis du har spørgsmål, så spørg din lærer; det kan sikkert hjælpe dig.
Artikler om emnet "Forenkle brøker"
Оцените, пожалуйста статью
Populær