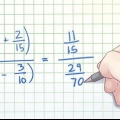
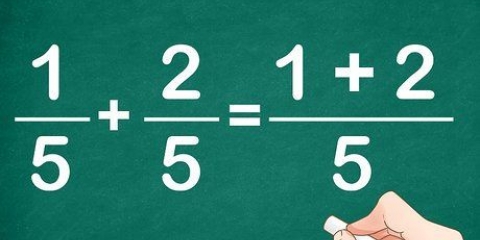Eksempel: x - 25 = (x+5)(x-5) 

Forenkling af matematiske brøker
Indhold
Matematiske eller algebraiske brøker virker i starten utrolig svære og kan virke skræmmende for den utrænede elev at tackle. Med en blanding af variabler, tal og endda eksponenter er det svært at vide, hvor man skal starte. Men heldigvis gælder de samme regler, der er nødvendige for at forenkle almindelige brøker, såsom 15/25, også for matematiske brøker.
Trin
Metode 1 af 3: Simplificering af brøker

1. Kend ordforrådet for matematiske brøker. Følgende udtryk vil blive brugt i eksemplerne og er almindelige i problemer med brøker:
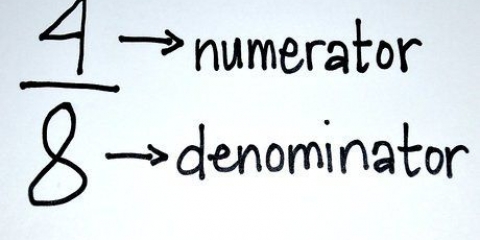
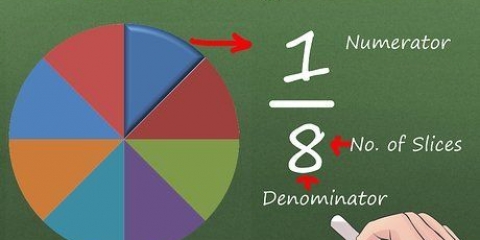
- Tæller: Den øverste del af en fraktion (f.eks. (x+5)/(2x+3)).
- Nævner: Den nederste del af en brøkdel (f. (x+5)/(2x+3)).
- Fællesnævner: Dette er et tal, som du kan dividere både tæller og nævner af en brøk med. For eksempel i brøken 3/9 er fælles divisor 3, da begge tal kan divideres med 3.
- Faktor:` Et tal, der ganges for at lave et andet tal. For eksempel: Faktorerne 15 er 1, 3, 5 og 15. Faktorerne for 4 er 1, 2 og 4.
- Forenklet ligning: Alle fælles faktorer fjernes og lige variable grupperes (5x + x = 6x), indtil du har opnået den enkleste form af en brøk, ligning eller opgave. Hvis du ikke kan gøre noget med brøken længere, er det forenklet.

2. Sammenlign hvordan man løser simple brøker. Dette er nøjagtig de samme trin, du vil tage for at løse matematiske brøker. Tag eksemplet, 15/35. For at forenkle en brøk, har vi brug for finde en fællesnævner. I dette tilfælde kan begge tal divideres med fem, så du kan strege de 5 ud fra brøken:
15→5 *3
35→5 *7
Nu kan du streg ud som udtryk. I dette tilfælde kan du strege de to femmere ud og efterlade dit forenklede svar, 3/7.
35→5 *7
Nu kan du streg ud som udtryk. I dette tilfælde kan du strege de to femmere ud og efterlade dit forenklede svar, 3/7.

3. Fjern faktorer fra algebraiske udtryk ligesom normale tal. I det foregående eksempel kunne du nemt fjerne 5`eren fra 15, og det samme princip gælder for mere komplekse udtryk som 15x - 5. Find en faktor, som begge tal har til fælles. Her er svaret 5, fordi man kan dividere både 15x og -5 med tallet fem. Som før fjerner du den fælles faktor og multiplicerer den med det, der er `tilbage`.`
15x - 5 = 5 *(3x - 1) For at tjekke dit arbejde skal du bare gange de fem tilbage i det nye udtryk - du ender med de samme tal, som du startede med.

4. Nu kan du slette komplekse termer ligesom simple termer. Det samme princip som med almindelige brøker fungerer også for matematiske brøker. Dette er den nemmeste måde at forenkle brøker på. Tag brøken:
(x+2)(x-3)
(x+2)(x+10)
Læg mærke til, hvordan udtrykket (x+2) vises i både tælleren (øverst) og nævneren (nederst). Som sådan kan du fjerne disse for at forenkle den algebraiske brøk, ligesom du fjernede 5`eren fra 15/35:
(x+2)(x-3)→(x-3)
(x+2)(x+10)→(x+10)
(x+2)(x+10)
Læg mærke til, hvordan udtrykket (x+2) vises i både tælleren (øverst) og nævneren (nederst). Som sådan kan du fjerne disse for at forenkle den algebraiske brøk, ligesom du fjernede 5`eren fra 15/35:
Metode 2 af 3: Simplificering af brøker

1. Find en fælles faktor i tælleren (den øverste del af brøken). Det første man skal gøre, når man forenkler en algebraisk brøk, er at forenkle hver del af brøken. Start med den øverste del og streg så mange tal over som muligt. Som eksempel vil vi bruge denne øvelse:
9x-3
15x+6
Start med tælleren: 9x – 3. Der er en fælles faktor for både 9x og -3, som er 3. Arbejd med de 3 udvendige beslag, som du ville gøre med ethvert andet tal, og efterlader 3*(3x-1). Dette er din nye tæller:
3 (3x-1)
15x+6
15x+6
Start med tælleren: 9x – 3. Der er en fælles faktor for både 9x og -3, som er 3. Arbejd med de 3 udvendige beslag, som du ville gøre med ethvert andet tal, og efterlader 3*(3x-1). Dette er din nye tæller:
15x+6

2. Find en fælles faktor i nævneren.Fortsætter eksemplet fra oven, isoler nævneren, 15x+6. Søg igen efter et tal, der passer til begge dele. Også her kan du udelade en faktor tre, så du står tilbage med 3 *(5x +2). Inkorporer din nye nævner i ligningen:
3 (3x-1)
3 (5x+2)
3 (5x+2)

3. Fjern lignende udtryk. Dette er stadiet, hvor du virkelig kan forenkle brøken. Tag alle led, der er i både tælleren og nævneren, og fjern dem. I dette tilfælde kan vi krydse de 3 ud fra både toppen og bunden.
3(3x-1)→(3x-1)
3(5x+2)→(5x+2)

4. Ved, hvornår ligningen er fuldstændig forenklet. En brøk er forenklet, når der ikke er flere fælles faktorer i toppen eller bunden. Husk, du kan ikke fjerne faktorer inde fra parentesen - i eksemplet kan du ikke faktorisere x`et af 3x og 5x, fordi de fulde udtryk faktisk er (3x -1) og (5x + 2). Så eksemplet er fuldstændig forenklet, med if det endelige svar:
(3x-1)
(5x+2)
(5x+2)

5. Prøv en øvelse. Den bedste måde at lære på er at blive ved med at forsøge at forenkle matematiske brøker. Svarene er under problemerne.
4(x+2)(x-13)
(4x+8) Svar: (x=13)
2x-x
5x Svar:(2x-1)/5
(4x+8)
5x
Metode 3 af 3: Tricks til at løse vanskeligere problemer

1. `Inverter` brøker til faktor med negative tal. Lad os sige, at vi har følgende ligning:
3(x-4)
5(4-x)
Bemærk hvordan (x-4) og (4-x) næsten er identiske, men du kan ikke strege dem ud, fordi de er omvendt. Dog kan (x - 4) skrives som -1 *(4 - x) på samme måde, som du omskriver (4 + 2x) som 2 *(2 + x). Dette kaldes "at bringe uden for parentesen".
-1 *3(4-x)
5(4-x)
Nu kan vi simpelthen udelade de to identiske (4-x):
-1 *3(4-x)
5(4-x)
Heraf følger det endelige svar: -3/5
5(4-x)
Bemærk hvordan (x-4) og (4-x) næsten er identiske, men du kan ikke strege dem ud, fordi de er omvendt. Dog kan (x - 4) skrives som -1 *(4 - x) på samme måde, som du omskriver (4 + 2x) som 2 *(2 + x). Dette kaldes "at bringe uden for parentesen".
5(4-x)
Nu kan vi simpelthen udelade de to identiske (4-x):
5
Heraf følger det endelige svar: -3/5

2. Genkend forskellen på to firkanter, mens du arbejder. Forskellen på to kvadrater er simpelthen at trække et kvadrattal fra et andet, ligesom udtrykket (a - b). Forskellen mellem perfekte kvadrater er altid forenklet i to dele, ved at lægge til og fratrække kvadratrødderne. Under alle omstændigheder kan du forenkle forskellen mellem perfekte firkanter på denne måde:
a - b = (a+b)(a-b) Dette kan være meget nyttigt, når du prøver at finde lignende udtryk i matematiske brøker.

3. forenkle polynomier. Polynomier eller polynomier er komplekse algebraiske udtryk med mere end to led, såsom: x + 4x + 3. Heldigvis kan mange polynomier forenkles ved at `faktorere`. Det foregående udtryk kan for eksempel omskrives som (x+3)(x+1).

4. Husk at variabler også kan faktoriseres. Dette er især nyttigt for udtryk med eksponenter, såsom x + x. Du kan udelade den største eksponent som en faktor. I dette tilfælde: x + x = x(x + 1).
Tips
- Tjek dit arbejde med faktorisering ved at gange faktoren tilbage i ligningen - du får det samme tal, som du startede med.
- Fjern altid de største tal, du kan, for fuldstændigt at forenkle din ligning.
Advarsler
- Glem ikke beregningsreglerne (rækkefølgen af operationer), ellers går det galt. Lær det derfor bedst muligt.
Artikler om emnet "Forenkling af matematiske brøker"
Оцените, пожалуйста статью
Populær