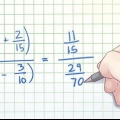
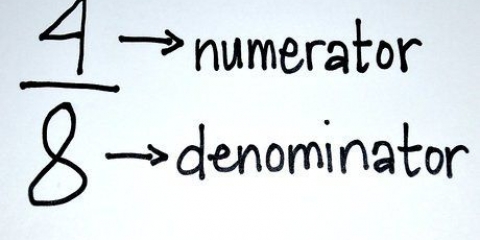
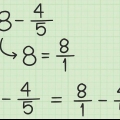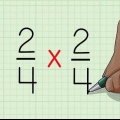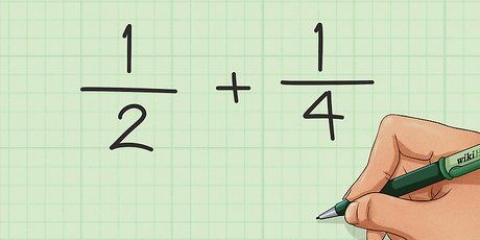Uanset om du skriver 1/5 + 2/5 eller 1+2/5, er svaret det samme: 3! Til sidst er 1 + 2 = 3. 
Så efter samme eksempel er nævneren 5. Det er alt! Dette er det nederste nummer af brøken og halvdelen af svaret! 
Hvad var tælleren? 3. Og nævneren? 5. Så 1/5 + 2/5 eller 1+2/5 er lig 3/5. 

Så 2/3 bliver 2/3 x 4 og 3/4 bliver 3/4 x 3. Det betyder, at vi nu har 2/12 og 3/12. Men vi er ikke færdige endnu! Du vil bemærke, at i dette tilfælde er nævnerne blevet ganget sammen. Dette virker i denne situation, men ikke altid. Nogle gange bliver du nødt til at lede efter mindre tal for at finde LCF. Og i andre tilfælde, med små tal, er alt du skal gøre at gange nævnerne sammen. 
Vi havde 2/3x4 og 3/4x3 som vores første trin - for at tilføje det andet trin er det faktisk 2 x 4/3 x 4 og 3 x 3/4 x 3. Det betyder, at 8/12 og 9/12 er vores nye tal. Perfekt! 
I dette eksempel gælder: 8+9/12 = 17/12. For at konvertere dette til et blandet tal skal du trække nævneren fra tælleren og se, hvad du står tilbage med. Det vil sige i dette tilfælde 17/12 = 1 5/12 

Lad os finde ud af, hvad er multiplerne af 12 og 8. Hvad er det mindste tal, som begge tal passer ind i?? 24. 8, 16, 24 og 12, 24 – bingo! 
Så 13 x 2/12 x 2 = 26/24. Og 17 x 3/8 x 3 = 51/24. Vi er nået langt for at løse problemet! 
26/24 + 51/24 = 77/24. Det var den pause, du ledte efter! Men disken er ret stor.... 
For dette eksempel: 24 går til 77. 3 gange.Så 24 x 3 = 72. Så er der en rest på 5 tilbage! Så hvad er dit endelige svar? 3 5/24. Det er alt!
Addere og trække brøker fra
Indhold
Tilføjelse og fratrækning af brøker er en vigtig færdighed at lære. Du støder på brøker overalt i hverdagen, især i matematiktimerne, fra folkeskole til universitet. Bare følg nedenstående trin for at lære, hvordan du tilføjer og trækker brøker, uanset om de er lige, ulige, blandede eller uægte brøker. Når du først har lært én måde, er alt andet meget nemmere!
Trin
Metode 1 af 3: Tilføjelse og subtrahering af brøker med samme nævner

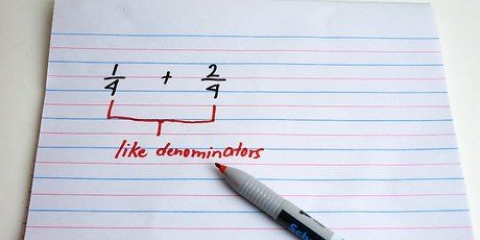
1. Skriv ligningen. Hvis nævneren af de to brøker, du tilføjer/fratrækker, er den samme, skal du også inkludere denne nævner i dit svar.
- Du behøver med andre ord ikke skrive 1/5 og 2/5 som 1/5 + 2/5 = ? Dette kan noteres som (1+2)/5 = ?. Nævneren er den samme og skal derfor kun nævnes én gang. Begge tællere er over resultatlinjen.

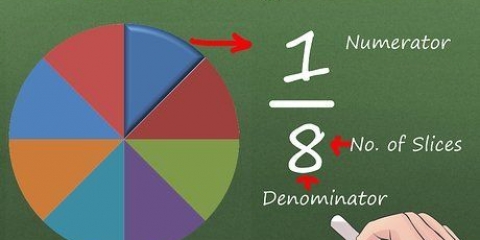
2. Læg tællerne sammen. Tælleren er tallet over brøklinjen. Tag følgende eksempel: 1/5 og 2/5; her er 1 og 2 vores tællere.

3. Lad nævneren være uændret. Intet at tilføje, trække fra osv., men uændret.

4. Skriv svaret ned. Nu skal du bare skrive svaret! Du vil se, at ifølge det foregående eksempel er svaret 3/5.
Metode 2 af 3: Tilføjelse og subtrahering af brøker med forskellige nævnere

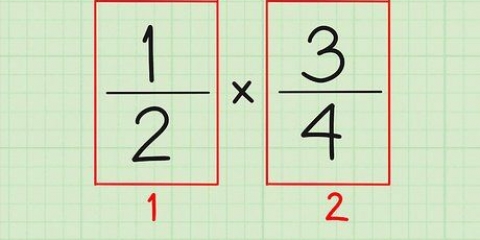
1. Find det mindste fælles multiplum (LCM) af nævnerne. Dette er det mindste tal, som begge nævnere har til fælles. Tag brøkerne 2/3 og 3/4. Hvad er nævnerne? 3 og 4. For at finde LCF for begge, brug en af følgende 3 måder:
- Skriv multiplerne ned. Multipletterne af 3 er 3, 6, 9, 12, 15, 18...og så videre. Multipletter af 4? 4, 8, 12, 16, 20 osv. Hvad er det laveste tal, der forekommer i begge sæt?? 12! Det er dit mindste fælles multiplum eller din kgv.
- Faktorisering i prime faktorer. Hvis du ved, hvad primfaktorer er, kan du bruge faktorisering. Her bestemmer du med hvilke primtal du kan gange et bestemt tal ved hjælp af multiplikation "at lave". For 3 er faktorerne 3 og 1. For 4 er primfaktorerne 2 og 2. Så gange du disse sammen, så 3 x 2 x 2 = 12. din kgf!
- Gang begge tal sammen for at fålille tal. I nogle tilfælde, som denne, kan du bare gange begge tal sammen – 3 x 4 = 12. Men hvis dine nævnere er store tal, kan dette ikke bare ske! Du kan ikke bare lave 56 x 44 og gå videre til 2464 som svar! Det er ikke forkert, men det er akavet.

2. gange nævneren med det tal, du skal bruge for at få lcg. Med andre ord vil du have, at hver nævner skal være det samme tal - kgv. For vores eksempel skal dette være 12. 4 x 3 = 12. Dette er nævneren for vores endelige svar.

3. Gang tælleren med det tal også. Hvis du gange nævneren af en brøk med et tal, skal du også gange tælleren med det samme tal. Det, vi gjorde i det sidste trin, var kun en del af den nødvendige multiplikation.

4. Tilføj (eller subtraher) tællere for at få dit svar. For at tilføje 8/12 til 9/12 skal du blot tilføje tællere sammen. Glem ikke: du lader nævneren være. Det tal, du opnåede med LCF, er din endelige nævner.
Metode 3 af 3: Tilføjelse og subtrahering af blandede og uægte fraktioner

1. Konverter dine blandede brøker til uægte brøker. En blandet brøk er et heltal med en brøk efter sig, som i eksemplet ovenfor (1 5/12). En uægte brøk er en brøk med en større tæller end nævneren. Et eksempel på dette er 17/12.
- Som eksempel tager vi 13/12 og 17/8.

2. Find fællesnævneren. Husk de tre måder at finde nævnernes lcg på? Ved at bestemme multiplerne, bruge primfaktorer eller ved at gange nævnerne sammen.

3. Gang tællerne med nævnerne for at få den lige brøkdel. Begge nævnere skal nu konverteres til 24. Sådan laver du 24 af 12? Gang det med 2. Fra 8 til 24? Gang det med 3. Men glem ikke, at du også skal gange tællerne!

4. Addere og trække brøker fra. Nu hvor begge brøker har samme nævner, kan du nemt tilføje eller trække begge brøker fra. Husk, lad nævneren være!

5. Gør dit svar til en blandet brøk. Sådan en stor tæller er lidt mærkelig og gør det svært at få en idé om størrelsen af din brøk. Alt du skal gøre for at løse det er at dividere tælleren med nævneren og bruge resten som tæller for din nye sammensatte brøk.
Artikler om emnet "Addere og trække brøker fra"
Оцените, пожалуйста статью
Populær