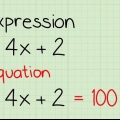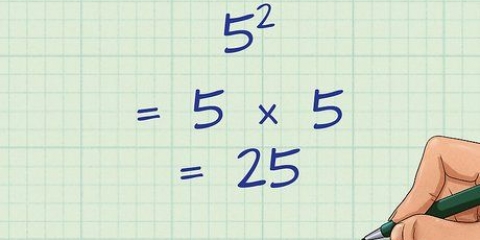Eksempel: følgende udtryk 2x + 4(5 + 2) + 3 - (3 + 4/2). Løs først for led i parentes, så 5 + 2 og 3 + 4/2. 5 + 2 = 7. 3 + 4/2 = 3 + 2 = 5. Udtrykket mellem det andet par parentes bliver 5, fordi vi først skal beregne 4/2 og først derefter regne additionen ud. Hvis vi blot ville arbejde fra venstre mod højre, så ville summen være 3 + 4 : 2, hvorved først 3 + 4 og derefter 7/2 ville blive beregnet, hvilket resulterer i det forkerte svar 7/2. Bemærk – hvis flere parenteser er indlejret (parenteser inden for parentes), opløs den inderste først og arbejd hen imod den yderste parentes. 
Efter at have løst parenteserne så eksemplet således ud. 2x + 4(7) + 3 - 5. Den eneste potens i vores eksempel er 3, og denne er lig med 9. Udtrykket bliver nu 2x + 4(7) + 9 - 5. 
Der er to gange i opgaven: 2x (2x er 2 × x) og 4(7). Vi kender ikke værdien af x, så lad os lade det være 2x. 4(7) = 4 × 7 = 28. Vi kan skrive dette anderledes som 2x + 28 + 9 - 5. 
Da vi allerede har løst et divisionsproblem, der stod i parentes, er der ingen divisionsproblemer tilbage i vores problem, så vi kan springe dette trin over. Dette rejser et vigtigt punkt - hvis en operation ikke forekommer i et udtryk, så fortsæt til den næste operation som angivet i matematikreglerne. 
Vores udtryk er nu delvist forenklet til "2x + 28 + 9 - 5". Nu lægger vi så meget sammen som muligt – fra venstre mod højre. Vi kan ikke lægge 2x til de andre tal, fordi vi ikke kender værdien af x, så vi springer denne over. 28 + 9 = 37, så vi kan omskrive udtrykket som "2x + 37 - 5". 
I vores udtryk, "2x + 37 - 5", der er kun én subtraktion,37 - 5 = 32 
Vores endelige svar er "2x + 32". Vi kan ikke løse tilføjelsen uden at kende værdien af x, men når vi først gør det, er det meget nemmere at løse end det oprindelige udtryk. 

Antag for eksempel, at vi skal løse brøken 36/60. Hvis vi har en lommeregner ved hånden, udregnes svaret (6) således. Hvis vi ikke har dette, kan vi komme langt ved at eliminere lignende faktorer. En anden måde at tænke på 36/60 er som (6 × 6)/(6 × 10). Dette kan igen omskrives til 6/6 × 6/10. 6/6 = 1, så vores udtryk bliver 1 × 6/10 = 6/10. Men vi er der ikke endnu – både 6 og 10 har samme faktor 2. Ved at gentage ovenstående procedure beholder vi3/5 om. 
Antag, at vi har udtrykket (3x + 3x)/(-3x + 15x).Denne brøk kan omskrives som (x + 1)(3x)/(3x)(5 - x), 3x forekommer i både tælleren og nævneren. Fjernelse af disse faktorer fra ligningen giver (x + 1)/(5 - x). Ligeledes er dette tilfældet med ligningen (2x + 4x + 6)/2. Da hvert led er deleligt med 2, kan vi omskrive det som (2(x + 2x + 3))/2 og dermed forenkle til x + 2x + 3. Husk, du kan ikke eliminere alle termer - kun de faktorer, der er i både tælleren og nævneren. For eksempel udtrykket (x(x + 2))/x, hvor "x" kan fjernes fra fraktionen, hvilket efterlader (x + 2)/1 = (x + 2). Men (x + 2)/x er ikke for at forenkle til 2/1 = 2. 
For eksempel kan udtrykket 3(x + 8 simplificeres til3x + 24, mens 3x(x + 8) kan forenkles til 3x + 24x. Bemærk, at i nogle tilfælde, såsom med variable brøker, kan konstanten uden for parentes bruges i forenklingen og skal derfor ikke ganges. For eksempel i brøken (3(x + 8))/3x forekommer faktoren 3 i både tælleren og nævneren, så vi kan annullere den og forenkle udtrykket til (x + 8)/x. Dette er enklere og nemmere at arbejde med end med (3x + 24x)/3x, hvilket ville have været svaret, hvis vi havde ganget. 
Se igen på udtrykket x - 5x + 6. Dette kan løses til (x - 3) (x - 2). Så hvis x - 5x + 6 er tælleren for en ligning med en af disse faktorer i nævneren (som i (x - 5x + 6)/(2(x - 2))), så kan vi indregne det i faktorer som f.eks. at vi kan slippe af med nævneren. Med andre ord, ved (x - 3)(x - 2)/(2(x - 2)), (x - 2) falder ud og efterlader os(x - 3)/2 tilovers. Som angivet ovenfor kan man også løse en ligning med faktorisering, især hvis den er sat lig nul. For eksempel: tag ligningen x - 5x + 6 = 0. Factoring giver os (x - 3)(x - 2) = 0. Da et tal gange nul er lig med nul, kan vi sætte begge led lig med nul for at finde svaret på dette problem. Så svaret på ligningen er x=3 og x= 2.
Forenkling af matematiske udtryk
Indhold
Matematikproblemer beder ofte om et svar "så enkelt som muligt" at skrive ned - med andre ord at give et svar så elegant som muligt. Mens et langt, klodset udtryk og en kortere, mere elegant udgave af det teknisk set betyder det samme, bliver et svar ofte ikke accepteret, før det er blevet forenklet så vidt muligt.Derudover er forenklede svar også nemmere at arbejde med. "Det er derfor, at lære at forenkle er en vigtig færdighed for fremtidige matematikere.
Trin
Metode 1 af 2: Rækkefølgen af matematiske operationer

1. Rækkefølgen af operationer. Når du forenkler matematiske udtryk, kan du ikke bare evaluere fra venstre mod højre. Visse operationer har forrang frem for andre og skal derfor udføres først. Hvis du ikke gør dette, kan du få det forkerte svar. Rækkefølgen af operationer i matematik er som følger: Parenteser, Eksponentiering og forankring, Multiplikation og Division, Addition og Subtraktion. En mnemonik til at huske denne sekvens er "Hvordan skal vi slippe af med det utilstrækkelige " eller "HMWVDOA".
- Bemærk, at selvom et grundlæggende kendskab til operationerne er tilstrækkeligt til at løse de fleste standardudtryk, er specielle teknikker nødvendige for at løse udtryk, der indeholder variabler, inklusive de fleste polynomier. Se metode to for mere information.

2. Start med at løse alle led i parentes. I matematik betyder parentes, at alle led, de omslutter, skal løses adskilt fra det omgivende udtryk. Uanset operationerne skal du først løse alle led i parentes, hvis du vil forenkle et udtryk. Husk, at regnereglerne for rækkefølgen af operationer også gælder i parentes. Så også her først parentes, derefter eksponentiering, etc.

3. Opløs nu beføjelserne. Efter at have udarbejdet parenteserne kan du nu gå videre til eksponentiering. Løs dem én efter én.

4. Løs nu multiplikationssummerne. Husk at en multiplikation kan skrives på flere måder. Med en prik, uden en prik eller med et ×-symbol. Men også sådan noget 4(x)) angiver en multiplikation.

5. Fortsæt med divisionsproblemer. Hvis du leder efter divisionsproblemer, så husk, at disse også kan skrives på forskellige måder. Det simple ÷ symbol , med et kolon eller en skråstreg (som f.eks 3/4) angiver alle en division.

6. Tilføj op. Læg nu de forskellige udtryk sammen. Arbejd dette fra venstre mod højre, som det er i udtrykket, og hvad der passer bedst. For eksempel, i summen 49 + 29 + 51 +71 er det lettere at opdele problemet i følgende blokke: 49 + 51 = 100, 29 + 71 = 100 og 100 + 100 = 200. Dette er lettere end 49 + 29 = 78, 78 + 51 = 129 og 129 + 71 = 200.

7. trække fra. Det sidste trin i operationerne er at trække de resterende vilkår fra. Træn resten af dit udtryk ud, fra venstre mod højre. Du kan tilføje negative tal i dette eller det foregående trin - det betyder ikke noget for dit svar.

8. Se dit udtryk. Efter at have gennemgået rækkefølgen af operationer står du tilbage med en række udtryk i den mest forenklede form. Hvis der er en eller flere variable i udtrykket, forbliver de stort set uændrede. Forenkling af udtryk med variable kræver, at vi løser disse ligninger yderligere for de ukendte, eller ved at bruge specielle metoder (se næste trin).
Metode 2 af 2: Simplificering af komplekse udtryk

1. Læg lige variable potenser sammen. Når man beskæftiger sig med udtryk, der indeholder variable, er det vigtigt at huske, at led med samme variabel og samme eksponent (eller "lige vilkår") kan lægges sammen (eller trækkes fra) som almindelige tal. Vilkårene skal ikke kun have den samme variabel, men også den samme eksponent. For eksempel kan 7x og 5x lægges sammen, men 7x og 5x kan ikke.
- Denne regel kan også udvides til multivariate termer. For eksempel kan 2xy tilføjes til -3xy, men ikke -3xy eller -3y.
- Tag følgende udtryk: x + 3x + 6 - 8x. I dette udtryk kan vi lægge vilkårene 3x og -8x sammen, fordi de er ens med hinanden. Vores udtryk bliver så forenklet: x - 5x + 6.

2. Forenkle brøker ved at eliminere eller dividere faktorer. Brøker, der kun består af tal (og ingen variable) kan forenkles på flere måder. En brøk er blot en divisionssum og skal behandles som sådan. Desuden, hvis den samme multiplikation forekommer i tælleren eller nævneren, kan den elimineres, fordi de allerede giver svar 1, når de deles. Med andre ord, hvis tælleren og nævneren begge har samme faktor, kan den fjernes fra brøken, hvilket forenkler resultatet.

3. Hvis du har at gøre med brøker, der indeholder variable, så prøv at eliminere variablerne. Disse udtryk giver unikke muligheder for at forenkle. Ligesom almindelige brøker giver variable brøker dig mulighed for at fjerne faktorer, der er i både tæller og nævner. Men i sidstnævnte tilfælde kan disse faktorer være tal såvel som variable.

4. Gang termerne i parentes med deres konstanter. Når man beskæftiger sig med variable led i parentes plus en konstant, kan multiplicering af ethvert led inde i parentesen med konstanten uden for parentesen resultere i et enklere udtryk.Det gælder både numeriske konstanter og konstanter med variable.

5. Forenkle ved at faktorisere. Dette er en teknik, der kan forenkle nogle ligninger. Når du faktoriserer, så tænk på noget, der er det modsatte af "gange parenteser" - nogle gange kan en ligning repræsenteres mere enkelt som to led ganget sammen end som en ligning. Dette gælder især, hvis du kan eliminere en del af ligningen med det. I visse tilfælde (såsom med andengradsligninger) kan du også løse selve ligningen med faktorisering.
Artikler om emnet "Forenkling af matematiske udtryk"
Оцените, пожалуйста статью
Populær