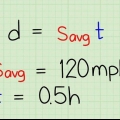Antag for eksempel, at udsagnet indikerer, at der er en beholder fuld af væske ved 295 K, hvis damptryk er lig med 1 atmosfære (atm). Spørgsmålet er: Hvad er damptrykket ved 393 K? Vi har to temperaturværdier og et tryk, så vi kan finde den anden trykværdi ved hjælp af Clausius-Clapeyron-ligningen. Erstat værdierne med variablerne, og vi får ln(1/P2) = (ΔHvap/R)((1/393) - (1/295)). Bemærk, at i Clausius-Clapeyron ligninger du altid Kelvin bruges som temperatur. Du kan bruge enhver enhed til tryk, så længe de er ens for både P1 og P2. 
Antag i vores eksempel, at vores væske er rent vand. Lad os se på en tabel med ΔHvap værdier, så ser vi, at ΔHvap ca. 40,65 KJ/mol er. Da vi bruger joule til værdien af H (i stedet for kilojoule), kan vi konvertere dette til `40.650 J/mol.` Indtastning af konstanterne i vores ligning giver ln(1/P2) = (40.650/8.314)((1/393) - (1/295)). 
Det eneste vanskelige punkt ved at løse vores ligning (ln(1/P2) = (40.650/8.314)((1/393) - (1/295))) omhandler den naturlige logaritme log(ln). Du kan eliminere dette ved at bruge begge sider af ligningen som styrken af den matematiske konstant e. Dermed: `ln(x) = 2 → e = e → x = e.` Nu kan vi løse vores ligning: ln(1/P2) = (40.650/8.314)((1/393) - (1/295)) ln(1/P2) = (4.889,34)(-0,00084) (1/P2) = e 1/P2 = 0,0165 P2 = 0,0165 = `60,76 atm.Dette ser ud til at holde stik - i et begrænset rum vil en hævning af temperaturen med næsten 100 grader (til næsten 20 grader mere end kogepunktet for vand) skabe en masse vanddamp, hvilket i høj grad øger trykket. 

Lad os i dette afsnit illustrere de begreber, vi diskuterer, med et simpelt eksempel. Antag, at vi ønsker at bestemme damptrykket af almindelig sirup. Generelt består almindelig sirup af en del sukker opløst i en del vand, så det kan vi sige sukker er det opløste stof og vand er opløsningsmidlet. Bemærk: Den kemiske formel for saccharose (granuleret sukker) er C12huh22O11. Dette bliver snart vigtigt. 
Som et eksempel, lad os sige, at den aktuelle temperatur af den almindelige sirup 298 K (ca. 25o C) er. 
Clausius-Clapeyron-ligningen kan være nyttig her - brug referencedamptrykværdien og 298 K (25o C) for henholdsvis P1 og T1. I vores eksempel er blandingen 25o C, så vi kan bruge de nemme referencetabeller. Vi ser, at vand ved 25o C har et damptryk på 23,8 mm HG 
Antag det for vores opskrift på sirup 1 liter (l) vand og 1 liter saccharose (sukker) er nødvendig. I så fald skal vi finde antallet af mol af hver. For at gøre dette bestemmer vi massen af hver, og konverterer derefter stoffets molære masse til antallet af Mol. Masse (1 l vand): 1000 gram (g) Masse (1 l for råsukker): ca. 1.056,7 g Mol (vand): 1000 gram × 1 mol / 18,015 g = 55,51 Mol Muldvarp (saccharose): 1.056,7 gram × 1 Mol/342,2965 g = 3,08 mol (bemærk, at du har molær masse af saccharose kan bestemme ved hjælp af den kemiske formel, C12huh22O11.) Samlet antal mol: 55,51 + 3,08 = 58,59 mol Molfraktion vand: 55,51/58,59 = 0,947 
Efter at have erstattet værdierne får du: sopløsning = (23,8 mm Hg)(0,947) sopløsning = `22,54 mm Hg.` Dette ser ud til at være korrekt - med hensyn til mol er kun lidt sukker opløst i en stor mængde vand (selvom de faktisk har samme volumen), så damptrykket vil kun falde en smule. 

Lad os for eksempel sige, at der er en ukendt væske med et damptryk på 25 torr ved 273 K og 150 torr ved 325 K, og vi ønsker at bestemme denne væskes fordampningsentalpi (ΔHvap). Vi kan løse dette, hvis: ln(P1/P2) = (ΔHvap/R)((1/T2) - (1/T1)) (ln(P1/P2))/((1/T2) - (1/T1)) = (ΔHvap/R) R × (ln(P1/P2))/((1/T2) - (1/T1)) = ΔHvap Nu udfylder vi vores værdier: 8,314 J/(K × Mol) × (-1,79)/(-0,00059) = ΔHvap 8.314 J/(K × Mol) × 3.033,90 = Hvap = 25.223,83 J/mol 
Antag for eksempel, at vi lavede en opløsning af to kemikalier: benzen og toluen. Det samlede volumen af opløsningen er 120 milliliter (ml); 60 ml benzen og 60 ml toluen. Temperaturen af opløsningen er 25o C, og damptrykket for hvert af disse kemikalier ved 25o C er 95,1 mm Hg for benzen og 28,4 mm Hg for toluen. Baseret på disse værdier skal du bestemme opløsningens damptryk. Vi kan gøre dette på følgende måde ved at bruge standarddensiteten, molmassen og damptrykket for vores to kemikalier: Masse (benzen): 60 ml = 0,060 l &gange 876,50 kg/1.000 l = 0,053 kg = 53 g Masse (toluen): 0,060 l &gange 866,90 kg/1.000 l = 0,052 kg = 52 g Mol (benzen): 53 g × 1 mol/78,11 g = 0,679 mol Mol (toluen): 52 g × 1 mol/92,14 g = 0,564 mol Samlet antal muldvarpe: 0,679 + 0,564 = 1,243 Molfraktion (benzen): 0,679/1,243 = 0,546 Molfraktion (toluen): 0,564/1,243 = 0,454 Løs: Popløsning = Pbenzenxbenzen + stoluenxtoluen sopløsning = (95,1 mmHg)(0,546) + (28,4 mmHg)(0,454) sopløsning = 51,92 mm Hg + 12,89 mm Hg = 64,81 mm Hg
Beregn damptryk
Indhold
Har du nogensinde hørt en let hvæsende lyd, når du åbner en flaske vand, som du har efterladt i den varme sol i et par timer? Dette er forårsaget af et princip kaldet Damptryk. I kemi er damptryk det tryk, der udøves på væggene i et lukket rum ved fordampning (omdannes til gas) af et stof. For at bestemme damptrykket ved en given temperatur, brug Clausius-Clapeyron-ligningen: ln(P1/P2) = (ΔHvap/R)((1/T2) - (1/T1)).
Trin
Metode 1 af 3: Anvendelse af Clausius-Clapeyron-ligningen

1. Skriv Clausius-Clapeyron-ligningen ned. Formlen til beregning af damptryk, der giver en ændring i damptryk over en periode, kaldes Clausius-Clapeyron-ligningen (opkaldt efter fysikerne Rudolf Clausius og Benoît Paul Émile Clapeyron). Dette er den formel, du normalt skal bruge for at løse almindelige damptryksproblemer i fysik- og kemitimer. Formlen ser således ud: ln(P1/P2) = (ΔHvap/R)((1/T2) - (1/T1)). I denne formel refererer variablerne til:
- Hvap: Entalpien for fordampning af en væske. Du kan normalt finde disse i en tabel bagerst i en lærebog i kemi.
- R: Den faktiske gaskonstant eller 8.314 J/(K × Mol).
- T1: Den temperatur, for hvilken damptrykket er kendt (dvs. starttemperaturen).
- T2: Den temperatur, som damptrykket skal bestemmes for (dvs. den endelige temperatur).
- P1 og P2: Damptrykket ved henholdsvis temperaturerne T1 og T2.

2. Erstat de variabler, du kender. Clausius-Clapeyron-ligningen ser vanskelig ud, fordi den indeholder så mange forskellige variabler, men det er egentlig ikke så svært, så længe du har den rigtige information. De enkleste damptryksproblemer giver dig to værdier af temperatur og værdien af et tryk eller to tryk og en temperatur - når du først har disse, er det en leg at løse dem.

3. Indtast konstanterne. Clausius-Clapeyron-ligningen indeholder to konstanter: R og ΔHvap. R er altid lig med 8.314 J/(K × Mol). Hvap (fordampningens entalpi), men det afhænger af det stof, du undersøger damptrykket for. Som nævnt ovenfor kan du bruge ΔHvap find værdier for et stort antal stoffer bagerst i kemi- eller fysikbøger, eller muligvis online (som f.eks, her.)

4. Løs ligningen. Når alle variabler er indtastet i ligningen (undtagen den variabel du vil løse), skal du fortsætte med at løse ligningen i henhold til almindelige algebraregler.
Metode 2 af 3: Bestemmelse af damptrykket med opløsninger

1. Skriv Raoults lov ned. I det virkelige liv er det sjældent, at du har at gøre med en enkelt ren opløsning - normalt har du at gøre med væsker, der er blandinger af forskellige forbindelser. Nogle af de bedst kendte af disse blandinger fremstilles ved at opløse en lille mængde af et bestemt kemikalie kaldet stof, der skal opløses i en stor mængde af et stof, det opløsningsmiddel (eller opløsningsmiddel) til en opløsning I disse tilfælde er det nyttigt at have kendskab til en ligning kaldet Raoults lov (efter fysikeren François-Marie Raoult), som ser ud som: sopløsning=Popløsningsmiddelxopløsningsmiddel. I denne formel refererer variablerne til:
- sopløsning: Damptrykket af den komplette opløsning (alle kombinerede komponentdele)
- sopløsningsmiddel: Opløsningsmiddeldamptryk
- xopløsningsmiddel: Molfraktionen af opløsningsmidlet.
- Bare rolig, hvis du bruger udtryk som "molfraktion" ved ikke – vi forklarer det i de næste par trin.

2. Identificer opløsningsmidlet og det opløste stof i din opløsning. Før du kan beregne damptrykket af en sammensat væske, skal du analysere de stoffer, du arbejder med. Som en påmindelse dannes en opløsning, når et stof opløses i et opløsningsmiddel - det kemikalie, der opløses, er altid det opløste stof, og det kemikalie, der opløses, er altid opløsningsmidlet.

3. Bestem opløsningens temperatur. Som vi så i afsnittet om Clausius Clapeyron ovenfor, vil temperaturen af en væske påvirke dens damptryk. Generelt gælder det, at jo højere temperatur, jo større damptryk - når temperaturen stiger, vil mere af væsken fordampe, hvilket øger damptrykket i det lukkede rum.

4. Bestem opløsningsmidlets damptryk. Kemiske referencematerialer har normalt damptrykværdier for mange almindelige stoffer og forbindelser, men disse gælder normalt kun ved temperaturer på 25°C/298K eller ved kogepunktet. Hvis opløsningens temperatur har en af disse værdier, kan du bruge referenceværdien; hvis ikke, skal du finde damptrykket ved den aktuelle temperatur.

5. Bestem molfraktionen af opløsningsmidlet. Det sidste, vi skal gøre, før vi kan løse, er at bestemme molfraktionen af opløsningsmidlet. At finde molfraktioner er meget simpelt: konverter bare komponenterne til mol, og find derefter procentdelen af de samlede mol i stoffet, som hver komponent optager. Med andre ord er molfraktionen af hver komponent lig med (antal mol af komponent) / (samlet antal mol af stoffet).

6. Løse. Nu har vi endelig alt, hvad vi behøver for at løse ligningen af Raoults lov. Denne del er overraskende enkel: Erstat værdierne for variablerne i den forenklede ligning af Raoults lov i begyndelsen af dette afsnit (sopløsning = Popløsningsmiddelxopløsningsmiddel).
Metode 3 af 3: Bestem damptrykket i særlige tilfælde

1. Vær opmærksom på standard temperatur- og trykforhold. Forskere bruger ofte en række faste værdier for temperatur og tryk, som en slags praktisk `standard`. Disse værdier kaldes standard temperatur og tryk (standardbetingelserne). Damptryksangivelser bruger ofte standardbetingelser, så det er nyttigt at huske disse værdier. Standard temperatur og tryk er defineret som:
- Temperatur: 273,15 K / 0 C / 32 F
- Travl: 760 mm Hg / 1 atm / 101.325 kilopascal

2. Bestil Clausius-Clapeyron-ligningen for at finde andre variable. I vores eksempel i del 1 så vi, at Clausius-Clapeyron-ligningen er meget nyttig til at finde damptrykket af rene stoffer. Men ikke alle spørgsmål vil handle om at bestemme P1 eller P2 - i mange tilfælde vil du blive bedt om at finde en temperaturværdi eller nogle gange endda en ΔHvap hvor er. Heldigvis er det ofte ikke mere end et spørgsmål om at omskrive ligningen, så den variabel, du løser for, er isoleret til den ene side af lighedstegnet.

3. Overvej damptrykket af det opløste stof, når det producerer damp. Ved at bruge eksemplet med Raoults lov ovenfor, producerer det opløste stof, sukker, ikke selv damp ved normale temperaturer (hvornår var sidste gang du så en skål sukker fordampe??) Men når det opløste stof ikke fordamper, vil det påvirke damptrykket. Vi kan demonstrere dette ved hjælp af en modificeret version af Raoults lov: sopløsning = Σ(Pkomponentxkomponent) Sigma-symbolet (Σ) betyder, at vi skal lægge damptrykket sammen for alle komponenterne for at finde svarene.
Tips
- For at bruge Clausius Clapeyrons ligning ovenfor, skal temperaturen måles i Kelvin (betegnet som K). Hvis temperaturen er angivet i grader Celsius, skal du konvertere den ved hjælp af følgende formel: tk = 273 + Tc
- Ovenstående metoder virker, fordi energi er direkte proportional med mængden af tilført varme. Væskens temperatur er den eneste miljøfaktor, som damptrykket afhænger af.
Artikler om emnet "Beregn damptryk"
Оцените, пожалуйста статью
Populær