Bemærk dog, at hvis de anvendte tidsenheder i din gennemsnitlige hastighedsværdi er forskellige fra dem i din tidsværdi, skal du konvertere den ene eller den anden for at matche. For eksempel, hvis en gennemsnitshastighed måles i km/t og tiden er i minutter, skal du dividere tiden med 60 for at omregne den til timer. Lad os løse vores prøveproblem. 120 km/t × 0,5 t = 60 km. Bemærk, at tidsenhederne (timer) fald væk mod enhederne i nævneren af gennemsnitshastigheden (timer), hvilket kun efterlader afstandsenhederne (km). 
Antag, at vi ved, at en bil har kørt 60 km på 50 minutter, men vi har ingen værdi for gennemsnitshastigheden under kørsel. I dette tilfælde kan vi bruge variablen sperle isolere i basisligningen for afstanden, og vi får sperle = d/t at få. Så beregner vi 60 km/50 minutter = 1,2 km/min. Bemærk, at i vores eksempel har vores svar for hastighed en usædvanlig enhed (km/minut). For at få dit svar i den mere almindelige form for km/t, gange det med 60 minutter/time og få `72 km/t at få. 
Eksempel: I eksemplet ovenfor konkluderede vi, at for at rejse 60 km på 50 minutter, skulle vi køre med 72 km/t. Dette er dog kun sandt, hvis vi kører med én hastighed på hele rejsen. For eksempel, ved at køre halvdelen af turen med 80 km/t og den anden halvdel med 64 km/t, kører vi stadig 60 km på 50 minutter — 72 km/t = 60 km/50 min = ????? Matematiske løsninger at bruge derivater er ofte et bedre valg end afstandsformlen til at definere et objekts hastighed i virkelige situationer, fordi ændringer i hastighed er sandsynlige. 

Bemærk, at denne formel bruger absolutte værdier (symbolet |). Absolutte værdier betyder blot, at termerne i symbolerne bliver positive, når de er negative. Lad os for eksempel sige, at vi stopper på en helt lige vejstrækning undervejs. Hvis der er en lille by 5 km foran os og en by 1 km bag os, hvor langt er de to byer så fra hinanden?? Hvis vi tager by 1 som x1 = betragte 5 og by 2 som x2 = -1, så kan vi finde d, afstanden mellem de to byer, som følger: d = |x2 - x1| = |-1 - 5| = |-6| = 6 km. 
Afstandsformlen i todimensionelt rum bruger Pythagoras sætning, som siger, at hypotenusen i en retvinklet trekant er lig med kvadratroden af de to andre sider. Lad os for eksempel sige, at vi har to punkter i x-y-planet: (3, -10) og (11, 7), som henholdsvis repræsenterer midten af en cirkel og et punkt på cirklen. For at finde den lige afstand mellem disse to punkter kan vi løse følgende: d = √((x2 - x1) + (y2 - y1)) d = √((11 - 3) + (7 - -10)) d = √(64 + 289) d = √(353) = 18,79 
Eksempel: Lad os sige det som en astronaut, der svæver i rummet nær to asteroider. Den ene er omkring 8 km foran os, 2 km til højre for os og 5 km under os, mens den anden er 3 km bag os, 3 km til venstre for os og 4 km over os. Hvis vi repræsenterer disse asteroiders positioner med koordinaterne (8.2,-5) og (-3,-3.4), kan vi finde afstanden mellem de to som følger: d = √((-3 - 8) + (-3 - 2) + (4 - -5)) d = √((-11) + (-5) + (9)) d = √(121 + 25 + 81) d = √(227) =15,07 km
Beregn afstand
Indhold
Afstand, ofte omtalt som variablen d, er et mål for det rum, der optages af en ret linje mellem to punkter. Afstand kan referere til mellemrummet mellem to stationære punkter (f.eks. er en persons højde afstanden fra bunden af hans eller hendes fødder til toppen af hans eller hendes hoved) eller kan henvise til mellemrummet mellem den aktuelle position af en bevægelig objektet og dets startplacering. De fleste afstandsproblemer kan løses med ligningerne d = sperle × t hvor d er afstanden, sperle middelhastigheden og t tiden eller ligningen d = √((x2 - x1) + (y2 - y1)), hvor (x1, y1) og (x2, y2) er x- og y-koordinaterne for to punkter.
Trin
Metode 1 af 2: Bestem distance med gennemsnitshastighed og tid

1. Bestem værdierne for gennemsnitshastighed og tid. Når man forsøger at finde den afstand, et bevægeligt objekt har tilbagelagt, er to oplysninger afgørende for at foretage denne beregning: fart` (eller hastighedsstørrelsen) ogtid hvor objektet blev flyttet. Med disse data er det muligt at finde den afstand, objektet har tilbagelagt, ved hjælp af formlen d = sperle × t.
- For bedre at forstå anvendelsen af afstandsformlen skal vi i dette afsnit løse et eksempelproblem. Lad os sige, at vi kører omkring 120 km/t og vil vide, hvor langt vi vil rejse om en halv time. Af 120 km/t som vores værdi for gennemsnitshastigheden og 0,5 time som vores værdi for tid, vil vi løse dette problem i næste trin.

2. Gang gennemsnitshastigheden med tiden. Når du kender gennemsnitshastigheden for et bevægeligt objekt og den tid, det tog at bevæge sig, er det relativt nemt at finde den afstand, den har tilbagelagt. Du skal bare gange disse to værdier sammen for at få dit svar.

3. Rediger ligningen for at løse de andre variabler. Enkelheden af den grundlæggende afstandsligning (d = sperle × t) gør det ret nemt at bruge ligningen til at finde værdierne af variable ud over afstand. Isoler den variabel, du vil løse i henhold til de grundlæggende regler for matematik, og indtast derefter værdierne af de to andre variabler for at finde værdien af den tredje. Med andre ord, for at finde gennemsnitshastigheden for dit objekt, skal du bruge ligningen sperle = d/t og for at finde den tid, et objekt har rejst, skal du bruge ligningen t = d/sperle.

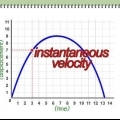
4. Bemærk, at variablen `sperle` i afstanden formlen henviser til gennemsnit fart. Det er vigtigt at forstå, at standardafstandsformlen giver et forenklet billede af et objekts bevægelse. Afstandsformlen antager, at det bevægelige objekt har en konstant hastighed har — med andre ord, det antager, at det bevægelige objekt bevæger sig med en `ensartet`, uforanderlig hastighed. For abstrakte matematiske problemer, såsom dem man støder på i et akademisk miljø, er det nogle gange stadig muligt at modellere et objekts bevægelse ved hjælp af denne antagelse. I det virkelige liv repræsenterer denne model dog ofte ikke nøjagtigt bevægelsen af objekter i bevægelse, som i virkeligheden kan accelerere, decelerere, stoppe og vende over tid.
Metode 2 af 2: Bestemmelse af afstanden mellem to punkter

1. Bestemmelse af to punkter i et fladt rum. Hvad hvis du i stedet for at bestemme afstanden et bevægende objekt har tilbagelagt, skal bestemme afstanden mellem to stationære objekter? I tilfælde som dette vil den hastighedsbaserede afstandsformel, der er beskrevet ovenfor, ikke være til nogen nytte. Heldigvis findes der en anden afstandsformel til hurtigt at finde den korteste afstand mellem to punkter. Men for denne formel skal du kende koordinaterne for de to punkter. Hvis du har at gøre med en endimensionel afstand (som på en tallinje), er dine koordinater to tal, x1 og x2. Hvis du har at gøre med afstand i to dimensioner, skal du bruge værdier for to punkter (x,y), (x)1,y1) og (x2,y2). For tre dimensioner skal du endelig have værdier for (x1,y1,z1) og (x2,y2,z2).

2. Bestem afstand på en linje ved at trække værdien af koordinaterne for de to punkter. Det er let at beregne den endimensionelle afstand mellem to punkter, hvis du kender værdien for hvert punkt. Bare brug formlen d = |x2 - x1|. I denne formel trækker du x fra1 ud af x2 og tag den absolutte værdi af dit svar for at finde afstanden mellem x1 og x2 at finde. Normalt bruger man den endimensionelle afstandsformel, når de to punkter ligger på en tallinje eller akse.

3. Find afstanden i planet ved hjælp af Pythagoras sætning. At finde afstand mellem to punkter i todimensionelt rum er mere kompliceret end i én dimension, men ikke svært. Bare brug formlen d = √((x2 - x1) + (y2 - y1)). I denne formel trækker du de to x-koordinater fra, kvadrerer resultatet, trækker y-koordinaterne fra, kvadrerer resultatet, adderer de to mellemliggende resultater og beregner kvadratroden for at finde afstanden mellem de to punkter, du skal finde. Denne formel fungerer i det todimensionelle plan - for eksempel på standard x/y-diagrammer.

4. Bestem den tredimensionelle afstand ved at ændre arealformlen. I tre dimensioner har punkter også en z-koordinat ud over x- og y-koordinaten. For at finde afstanden mellem to punkter i tredimensionelt rum, brug d = √((x2 - x1) + (y2 - y1) + (z2 - z1)). Dette er en modificeret form af den ovenfor beskrevne todimensionelle afstandsformel, der også tager hensyn til z-koordinaterne. Ved at trække de to z-koordinater fra hinanden, kvadrere dem og køre gennem resten af formlen som beskrevet ovenfor, vil du være sikker på, at dit endelige svar afspejler den tredimensionelle afstand mellem de to punkter.
Artikler om emnet "Beregn afstand"
Оцените, пожалуйста статью
Populær